【题解】SCOI2009围豆豆

最新推荐文章于 2022-11-20 14:56:42 发布

转载最新推荐文章于 2022-11-20 14:56:42 发布 · 120 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/twilight-sx/p/9122212.html

本文介绍了一种判断点是否位于多边形内的射线法，并结合SPFA算法解决了一个涉及状态转移的问题。通过引入射线法的概念，讨论了如何有效判断豆豆的位置状态，同时利用SPFA算法进行状态转移。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

　　很久之前就很想做的一道题，一直思考到今天才下定决心看题解。这道题中，很关键的一点就在于：如何判断一个点是否在一个多边形内？其实如果计算几何基本功扎实的话，应该是可以很快给出答案的（可惜我完全不行）：由一个点向一边引一条射线，判断与多边形相交的边数。若边数是奇数，说明在多边形的内部。在这里贴一篇博文：大佬的博客。

　　以下想图解一下射线法（与代码判图方式一致）。

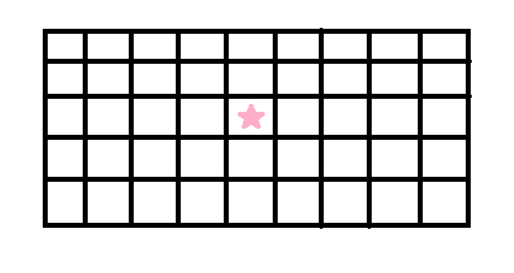
　　1.图中五角星为一个豆豆。

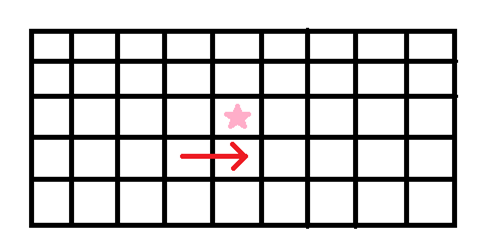
　　2.在转移的时候，我们由\(f[i][j][k] -> f[i][j + 1][k']\) 的转移即为在这两个格子之间链接一条边界线。

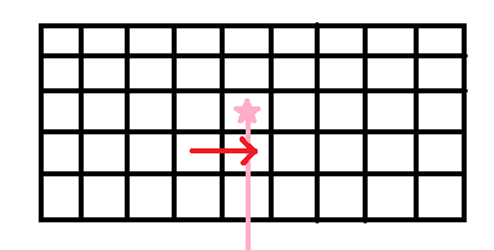
　　3.再转移一下，我们会注意到此时这个豆豆向下引的射线与两条边界线均有交点，但它暂时是被包围的状态，与我们所设的状态矛盾。所以我们规定：只有与箭头头部相交才算做一次。

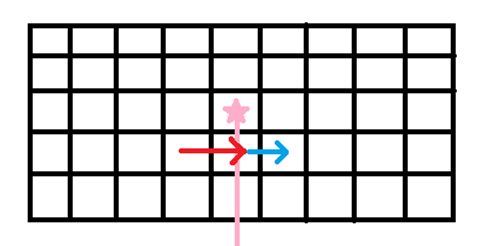
　　4.如果再次出现，次数变成偶数，就不在边界内了：

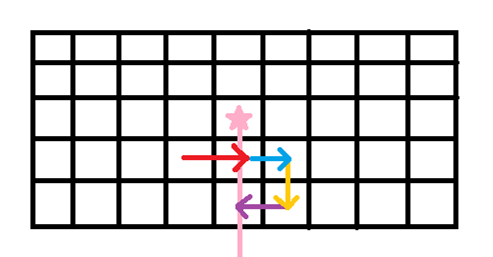
　　通过这几幅图，我们会发现竖直方向的移动不会改变豆豆是否被包围的判定，可以不必重复判断。了解了这一点之后，我们每一次的转移都是在画轮廓线。我们规定状态 \(f[i][j][k]\) 表示当前边界线画到第 \(\left ( i,j \right )\)时，被包围的豆豆状况为 \(k\) 时的最大得分。因为 \(\left ( i,j \right )\) 可以转移到 \(\left ( i,j + 1 \right )\)，反之亦然，所以这个转移是不满足拓扑序的。但由于它满足三角形不等式，所以我们使用spfa来转移状态。由于题目规定移动会减少分数，所以不用担心存在正环的问题。

#include <bits/stdc++.h>
using namespace std;
#define maxn 20
#define maxk 6000
#define INF 99999999
int n, m, S, Map[maxn][maxn];
int ans, CNST, val[maxn];
int f[maxn][maxn][maxk];
const int dx[4]={0, 0, -1, 1};
const int dy[4]={-1, 1, 0, 0};
bool vis[maxn][maxn][maxk];

struct node 
{
    int x, y, num;
    node(int xx = 0, int yy = 0, int zz = 0) { x = xx, y = yy, num = zz; }
}; queue <node> q;
node p[maxn];

int read()
{
    int x = 0, k = 1;
    char c;
    c = getchar();
    while(c < '0' || c > '9') { if(c == '-') k = -1; c = getchar(); }
    while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
    return x * k;
}

void spfa(int sx, int sy)
{
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++)
            for(int k = 0; k < CNST; k ++)
                f[i][j][k] = -INF;
    q.push(node(sx, sy, 0)), f[sx][sy][0] = 0, vis[sx][sy][0] = 1;
    while(!q.empty())
    {
        node now = q.front(); q.pop();
        vis[now.x][now.y][now.num] = 0;
        if(now.x == sx && now.y == sy)
            ans = max(ans, f[now.x][now.y][now.num]);
        for(int k = 0; k < 4; k ++)
        {
            int xx = now.x + dx[k], yy = now.y + dy[k];
            if(xx <= 0 || xx > n || yy <= 0 || yy > m || Map[now.x][now.y]) continue;
            int num = now.num, Y = max(yy, now.y), del = 0;
            if(k <= 1)
            {
                for(int i = 1; i <= S; i ++)
                    if(p[i].y == Y && p[i].x < xx) 
                    {
                        num ^= 1 << (i - 1);
                        if((num >> i - 1) & 1) del += val[i];
                        else del -= val[i];
                    }
            }
            if(f[xx][yy][num] < f[now.x][now.y][now.num] + del - 1)
            {
                f[xx][yy][num] = f[now.x][now.y][now.num] + del - 1;
                if(!vis[xx][yy][num]) vis[xx][yy][num] = 1, q.push(node(xx, yy, num));
            }
        }
    }
}

int main()
{
    n = read(), m = read(), S = read();
    CNST = (1 << S) - 1;
    for(int i = 1; i <= S; i ++) val[i] = read();
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++)
        {
            char c; cin >> c;
            if(c == '#') Map[i][j] = -1;
            else Map[i][j] = c - '0';
            if(Map[i][j] >= 1) p[Map[i][j]] = node(i, j);
        }
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++)
            if(!Map[i][j]) spfa(i, j);
    printf("%d\n", ans);
    return 0; 
}

转载于:https://www.cnblogs.com/twilight-sx/p/9122212.html