Manacher算法

最新推荐文章于 2025-03-19 15:18:32 发布

阅读量44

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/DavidJing/p/10666837.html

本文详细介绍Manacher算法，一种高效求解回文字符串问题的方法。通过插入特殊字符转换原始字符串，利用回文串的对称性减少重复计算，实现接近线性的复杂度。

Manacher算法

马拉车算法，用来解决回文字符串问题。

直接进入正题，manacher算法共分以下步骤。

1.由于奇数串和偶数串的区别，在两两字符之间插入'#'作为间隔。开头插入'@'，结尾插入'$'防止越界。

2.分类讨论，计算以某个点为中心点所能扩展出的最大回文串。

其中设maxright为目前已知能扩展最右的串的最右端点，pos为这个能扩展最右的串的中心点。

循环枚举中心点i,计算能扩展的最大长度len[i]。

第一类：i<=maxright

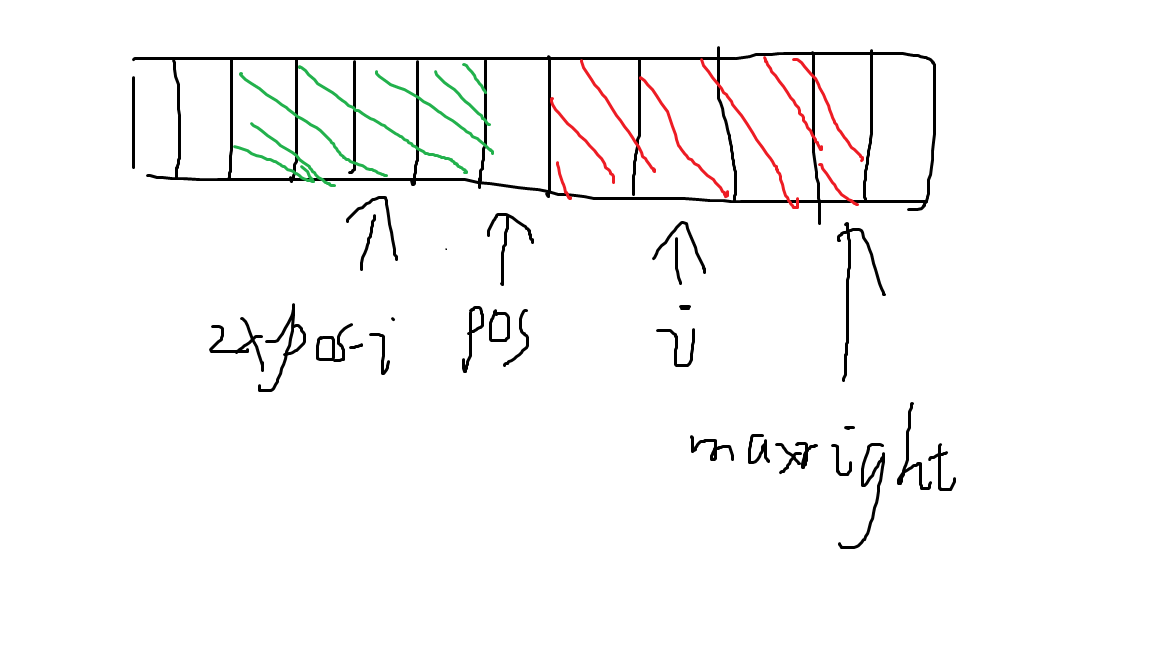
由于回文串的对称性，红色部分是完全等于绿色部分的。而i对应点即为2$\times$pos-i，所以i目前能扩展的长度是和2$\times$pos-i是一样的。（最远不超过maxright,因为超过部分不满足对称)

那么超过maxright部分怎么办呢？--暴力枚举判断

第二类:i==maxright+1

此时无法通过对称性，同上，暴力判断。

在计算完后更新maxright和pos。

复杂度接近于线性~~(然而我不会证)~~

3.最后以原串的最长回文字符串长度即为max(len[i]-1)

#include<bits/stdc++.h>
using namespace std;
int LEN,ans;
string s;
char st[22000005];
int len[22000005];
int init(string s)
{
    st[0]='@';int lens=s.length();
    for(int i=0;i<=lens-1;i++)
    st[i*2+1]='#',st[i*2+2]=s[i];
    st[lens*2+1]='#';st[lens*2+2]='$';
    return lens*2+1;
}
void Manacher()
{
    int maxright=0,pos=0;
    for(int i=1;i<=LEN;i++)
    {
        if(i<=maxright) len[i]=min(len[2*pos-i],maxright-i+1);
        else len[i]=1;
        while(st[i+len[i]]==st[i-len[i]])len[i]++;
        if(i+len[i]-1>maxright){pos=i;maxright=i+len[i]-1;}
        ans=max(ans,len[i]);
    }
}
int main()
{
    cin>>s;
    LEN=init(s);
    Manacher();
    printf("%d",ans-1);
    return 0;
}

转载于:https://www.cnblogs.com/DavidJing/p/10666837.html