Java-Manacher算法

Only you680

于 2025-01-16 14:43:38 发布

阅读量898

点赞数 42

分类专栏： java 文章标签：算法

本文链接：https://blog.youkuaiyun.com/weixin_56812051/article/details/145028290

版权

java 专栏收录该内容

27 篇文章

订阅专栏

回文子串：指的是一个字符串正着读和反着读是一样的，就叫回文子串，比如abccba。

最长回文子串：即一个字符串中最长的回文子串，比如abcwe12344321ewcbdrt。每个字符自身是回文的。

那么如何得到一个字符串中最长的回文子串长度呢（知道长度和中心位置很容易得到具体的最长子串）？

一、暴力中心拓展方法

以字符串每个位置的字符为中心向两边扩，能扩到的最大范围就是该字符的最长回文子串，遍历为整个字符串，算出每个位置的最长回文子串，就可以得到整个字符串最长的回文子串。

比如奇数长度的字符串：abcecba，0位置1，1位置1，2位置1，3位置7，4位置1,5位置1，6位置1。所以整个字符串的最长回文子串长度是7。

比如偶数长度字符串：abccba，0位置1，1位置1，2位置1，3位置1，4位置1,5位置1，6位置1。所以整个字符串的最长回文子串长度是1。但实际该字符串的最长回文子串长度是6。

我们发现偶数长度的字符串，用中心扩展法的时候，会匹配不到回文串。为了解决此问题，在处理最长回文子串的问题中，我们可以先预处理一下字符串，做一个填充，规避到偶数字符串匹配的问题。填充后的字符串长度一定是奇数；并且填充什么字符都可以，不会影响最后的结果（因为每次比较一定是真实字符两两比较、填充字符两两比较，不会存在真实字符和填充字符比较的时候）。

public String fill(String s){
    int N=s.length();
    StringBuffer sb=new StringBuffer();
    for (int i = 0; i < s.length(); i++) {
        sb.append("#");
        sb.append(s.charAt(i));
    }
    sb.append("#");
    return sb.toString();
}

偶数长度字符串：abccba，经过填充变为：#a#b#c#c#b#a#。此时用中心扩展发，0位置1，1位置3，2位置1，3位置3，4位置1，5位置3，6位置13，7位置3，8位置1，9位置3，10位置1，11位置3，12位置1。所以整个填充后的字符串的最长回文子串长度是16。实际该字符串的最长回文子串长度是13/2=6。完美解决问题。那么我们来看下暴力中心扩展法的代码。

public String findLongestPalindrome(String s){
    String res=fill(s);
    char[] ch=res.toCharArray();
    int N=res.length();
    int i=0;
    //最长回文子串的中心位置
    int maxC=0;
    //最长回文子串长度
    int maxLen=1;
    while(i<N){
        //i为中心开始拓展的位置
        int L=i-1;
        int R=i+1;
        //拓展不能越界
        while(L>=0&&R<N){
            if(ch[L]==ch[R]){
                L--;
                R++;
            }else{
                //只要不相等就跳出循环
                break;
            }
        }
        //以i为中心的最长回文子串的长度
        int curLen=R-L-1;
        if(curLen>maxLen){
            //更新最长长度
            maxLen=curLen;
            //更新中心位置
            maxC=i;
        }
        //循环求下一个位置的最长回文子串长度
        i++;
    }
    return res.substring(maxC-maxLen/2+1,maxC+maxLen/2).replaceAll("#","");
}

5. 最长回文子串 - 力扣（LeetCode）测试可过。

二、Manacher算法

Manacher算法的整体过程和暴力中心扩展算法是一样的，只不过在中间求解每个位置的最长回文子串长度的时候有优化加速。

我们再看一下上面的例子。偶数长度字符串：abccba，经过填充变为：#a#b#c#c#b#a#。此时用中心扩展发，0位置1，1位置3，2位置1，3位置3，4位置1，5位置3，6位置13，7位置3，8位置1，9位置3，10位置1，11位置3，12位置1。可以发现关于6位置对称的位置，其回文子串长度相等。说明肯定有一些规律在里面（看完Manacher算法就知道确实存在规律，存在何种规律）。下面我们就看下Manacher算法的步骤。

1、了解定义

回文右边界R：当前最长回文字符串拓展到的最远右边界。

回文中心C：一定是某个位置的最长回文子串将回文右边界拓展到了当前最远，那这个位置就是回文中心（回文中心和回文右边界同步更新）。

回文半径：以i为中心的最长回文字符串长度的一半+1，比如aba，b的回文半径是3/2+1=b到左侧a包含的字符个数=b到左侧a包含的字符个数=2。

回文半径数组：p[i]，i位置的回文半径。

2、如何求某个位置的（最长）回文半径

a、i位置在回文右边界外，暴力中心扩展

b、i位置在回文右边界里（那么一定有C<i<R这样的位置关系）

b1、情况一，i关于C对称的左侧位置i`的回文半径在C的回文半径内部（如下图）。此时i的回文半径i`的回文半径。

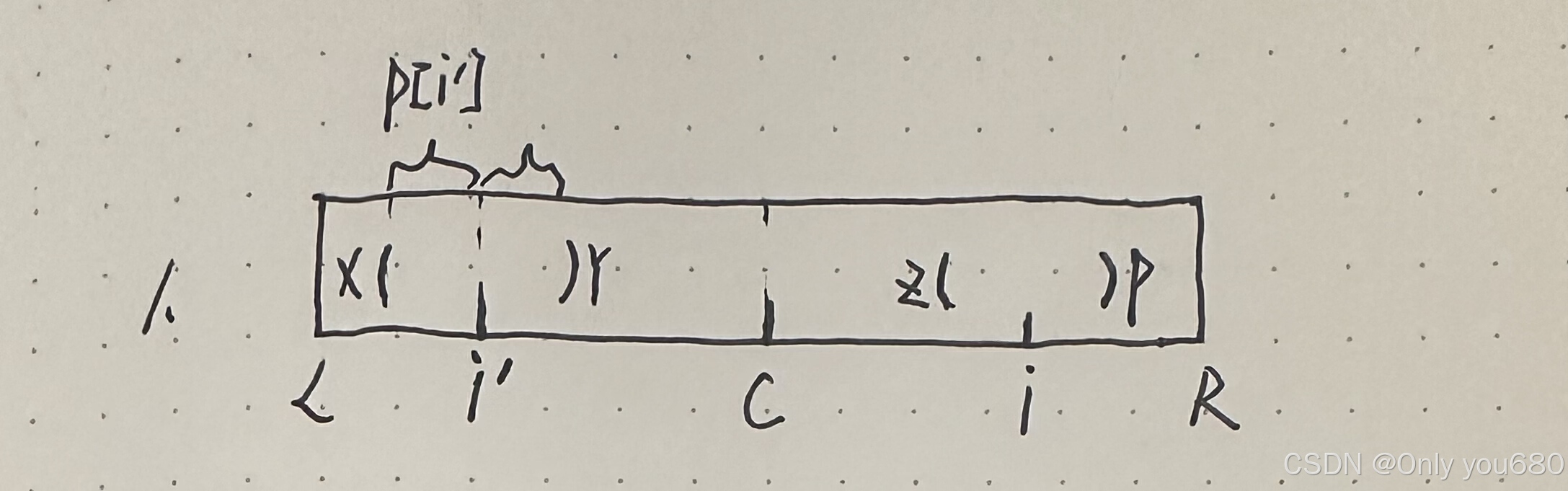
怎么证明呢？如图所示，根据i`的回文半径可知，x!=y，根据C的回文半径可知，x=p且y=z。所以z!=p。所以i的回文半径不能在扩展，等于p[i`]。

b2、情况二，i关于C对称的左侧位置i`的回文半径在C的回文半径外部（如下图）。此时i的回文半径p[i]=R-i。

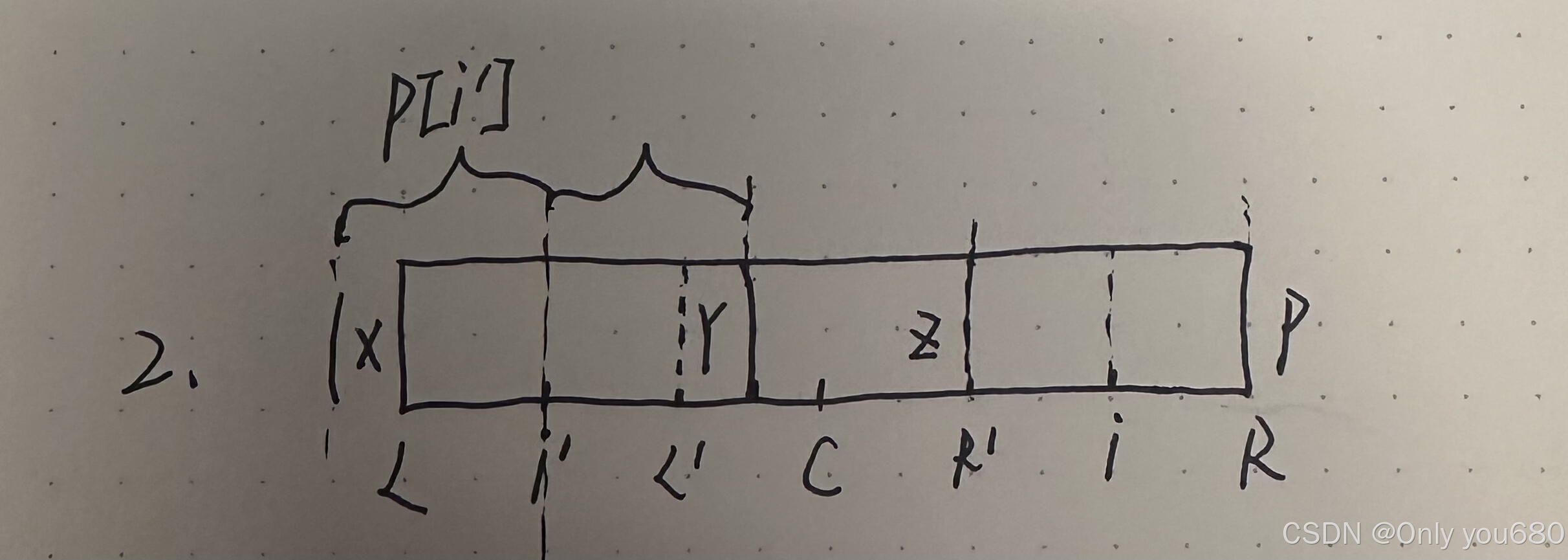
证明：根据i`的回文半径可知，x=y，根据C的回文半径可知，y=z且x!=p，所以可得z!=p。所以i的回文半径不能在扩展，等于p[i`]。

b3、情况三，i关于C对称的左侧位置i`的回文半径落在C的回文半径边界（如下图）。此时i的回文半径至少是R-i。能不能再扩展，未知。

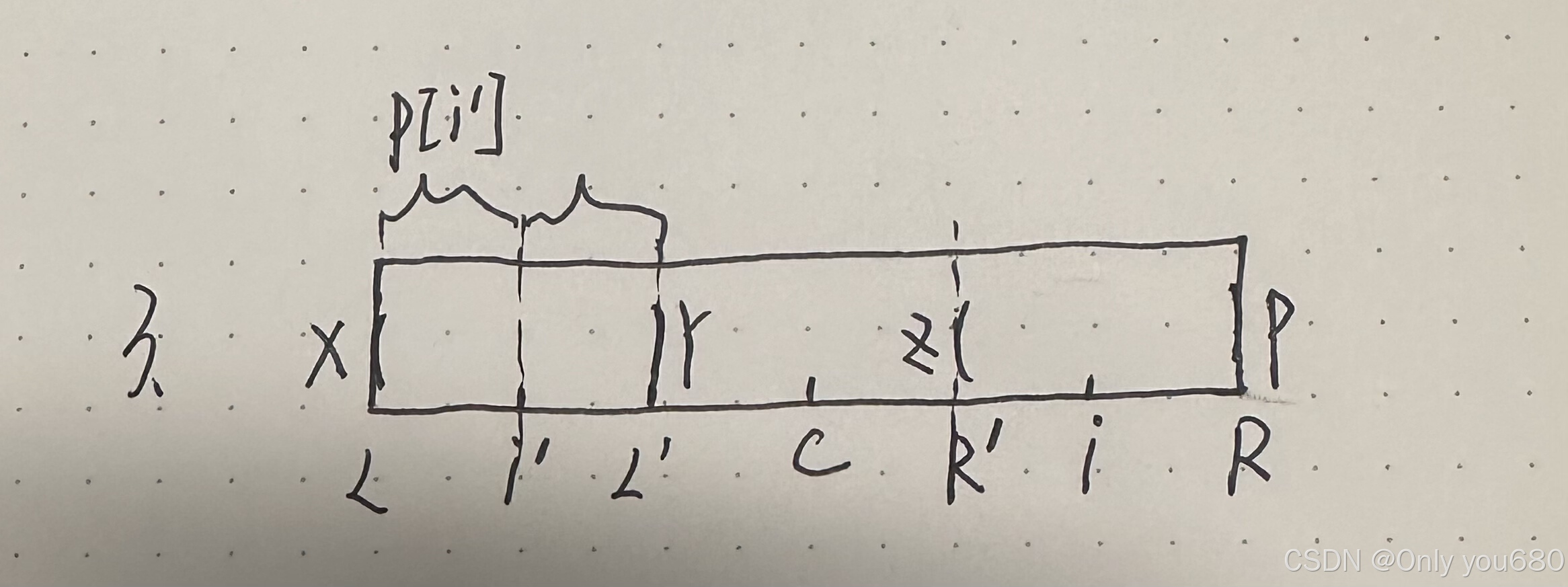
证明：根据i`的回文半径可知，x!=y，根据C的回文半径可知，y=z且x!=p，所以可得z!=x，但是z和p的关系无法知道，需要进一步去验证，所以i的回文半径至少是R-i。

以上我们就讨论了全部的位置关系，这样就可以依次算出每个位置的回文半径，即可得出最长回文半径和其中心点，然后得到最长回文子串。下面看代码。

public String manacher(String s){
    String res=fill(s);
    int N=res.length();
    char[] ch=res.toCharArray();
    //回文右边界
    int R=-1;
    //回文中心
    int C=-1;
    //回文半径数组
    int[] p=new int[N];
    int i=0;
    //最长回文半径
    int maxLen=0;
    //最长回文半径中心
    int maxC=0;
    while(i<N){
        if(i>=R){
            //i不在回文右边界里，回文半径至少为1，暴力扩
            p[i]=1;
            int iL=i-p[i];
            int iR=i+p[i];
            while(iL>=0&&iR<N){
                if(ch[iL]==ch[iR]){
                    p[i]++;
                    iL--;
                    iR++;
                }else{
                    break;
                }
            }
        }else{
            //i在回文右边界里
            int i_=C-(C-i);//i关于C的对称位置
            if(p[i_]<R-i){
                //对称点的回文半径在C的回文半径内部
                p[i]=p[i_];
            }else if(p[i_]>R-i){
                p[i]=R-i;
            }else{
                p[i]=R-i;
                int iL=i-p[i];
                int iR=i+p[i];
                while(iL>=0&&iR<N){
                    if(ch[iL]==ch[iR]){
                        p[i]++;
                        iL--;
                        iR++;
                    }else{
                        break;
                    }
                }
            }
        }
        //看此时的回文右边界是否被扩展
        if(i+p[i]>R){
            R=i+p[i];
            C=i;
        }
        //更新最长回文半径记录
        if(p[i]>maxLen){
            maxLen=p[i];
            maxC=i;
        }
        i++;
    }
    return res.substring(maxC- maxLen+1 , maxC+ maxLen).replaceAll("#", "");
}

上面的代码严格按照情况分支编写的，会发现有一些重复代码（两种需要暴力扩的情况代码重复）。下面看一个精简版的代码。

public String manacher(String s){
    String res=fill(s);
    int N=res.length();
    char[] ch=res.toCharArray();
    //回文右边界
    int R=-1;
    //回文中心
    int C=-1;
    //回文半径数组
    int[] p=new int[N];
    int i=0;
    //最长回文半径
    int maxLen=0;
    //最长回文半径中心
    int maxC=0;
    while(i<N){
        int i_=C-(C-i);
        //i在R外部，i的回文半径至少是1;i在R的内部时，回文半径至少是Math.min(R-i,p[i_])。
        p[i]=i>=R?1:Math.min(R-i,p[i_]);
        //然后我们不去讨论直接暴力扩当前的回文半径
        //根据我们的分析，其中两种情况一定会扩失败
        int iL=i-p[i];
        int iR=i+p[i];
        while(iL>=0&&iR<N){
            if(ch[iL]==ch[iR]){
                p[i]++;
                iL--;
                iR++;
            }else{
                break;
            }
        }
        //看此时的回文右边界是否被扩展
        if(i+p[i]>R){
            R=i+p[i];
            C=i;
        }
        //更新最长回文半径记录
        if(p[i]>maxLen){
            maxLen=p[i];
            maxC=i;
        }
        i++;
    }
    return res.substring(maxC- maxLen+1 , maxC+ maxLen).replaceAll("#", "");
}

至此，Manacher算法的全部内容就讲完了。