《坐热板凳》第八次团队作业：Alpha冲刺（第一天）

最新推荐文章于 2025-09-09 22:58:36 发布

weixin_30897233

最新推荐文章于 2025-09-09 22:58:36 发布

阅读量143

点赞数

CC 4.0 BY-SA版权

文章标签： java

原文链接：http://www.cnblogs.com/happiers/p/11014117.html

坐热板凳组在6月14日召开了第一次会议，确定了个人记账本微信小程序的项目方向和目标功能，进行了任务分工。团队正在学习软件测试基础技术和Scrum迭代式增量软件开发过程，面对Maven操作不熟练和内部沟通挑战，团队成员正积极应对。

《坐热板凳》第八次团队作业：Alpha冲刺

项目	内容
这个作业属于哪个课程	http://www.cnblogs.com/nwnu-daizh/
这个作业的要求在哪里	https://www.cnblogs.com/nwnu-daizh/p/11012922.html
团队名称	坐热板凳组
作业学习目标	①掌握软件测试基础技术。②学习迭代式增量软件开发过程（Scrum）
团队博客地址	https://www.cnblogs.com/happiers//
项目名称	个人记账本（微信小程序）

任务一前言：
第1次会议在6月14日在教七306召开。
主要确定了项目方向和目标功能，进行了任务分工，时长80min。

任务二团队项目 github地址：

github地址： https://github.com/jessiyx/sethotchair

任务三燃尽图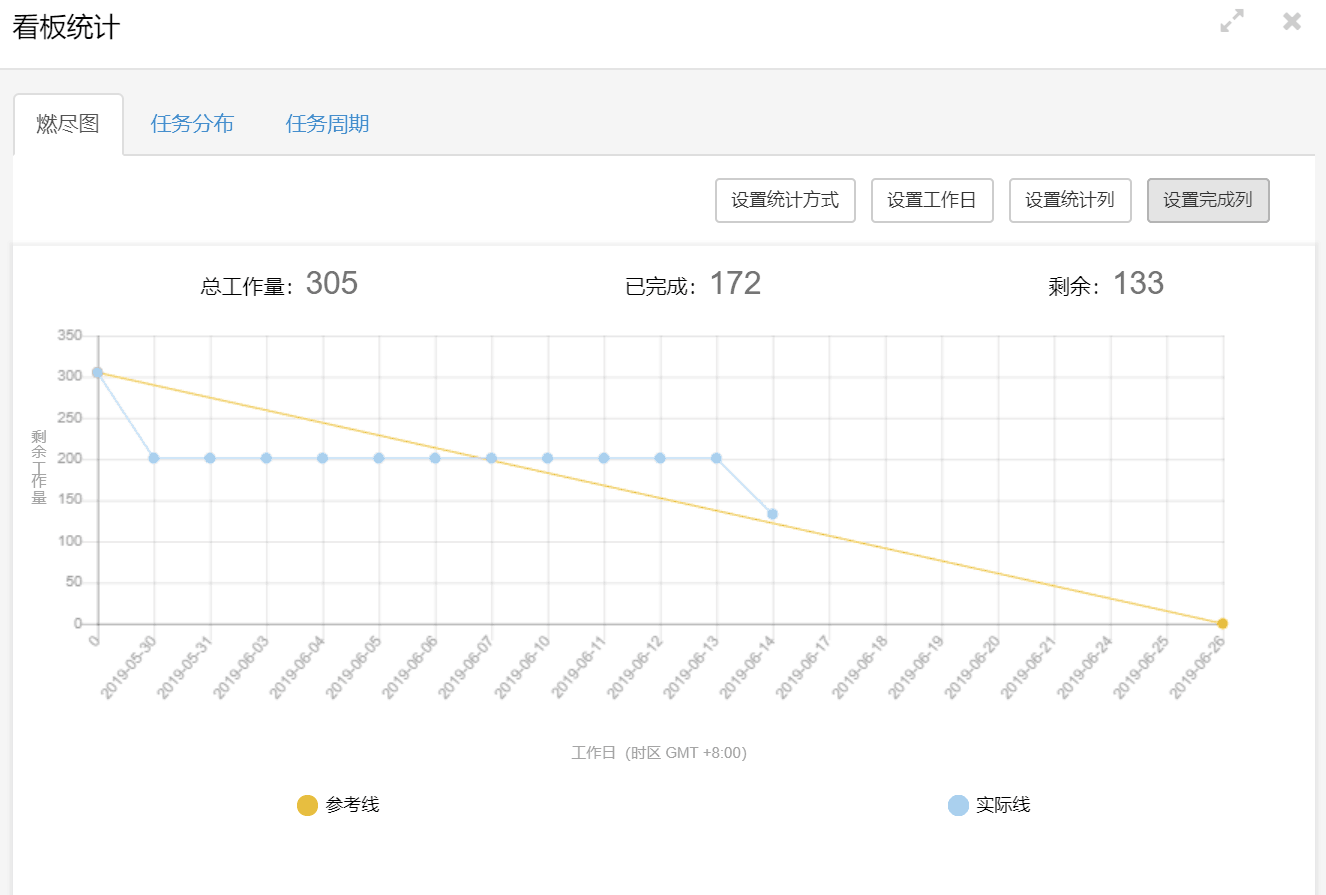

任务四站立会议照片

任务五具体分工

项目成员	具体任务
朱艺璇	负责给组员分配任务，汇总scurm meeting；组织协调任务进度
王潇	主要负责项目开发，学习相关内容
达星斗	编写博客，整理第一次会议内容
刘振华	协助完成开发，保证项目的顺利进行

任务六遇到的困难
（1）.不太熟练Maven的操作，导致项目进程有点滞后。
（2）.组员之间意见发生分歧，需要进行更好的沟通。

转载于:https://www.cnblogs.com/happiers/p/11014117.html