（专题二）05 矩阵的存储方式

矩阵的存储方式

完全存储方式和稀疏存储方式

矩阵A的存储方式

第一行第一列---的元素-----1

。。。

第3行第4列---的元素-----7

完全存储方式与稀疏存储方式之间的转化

先将转化为稀疏存储方式A

再将A转化为完全存储方式B

比较A,B 的存储，可以发现，矩阵规模加大，所需内存也变大

例如A描述的是一个稀疏矩阵

红色圈住的表示第二行第四列存储的是3

现在用spconvert()函数将矩阵转换为一个稀疏存储矩阵

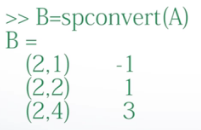
例子：

建立A矩阵，A有三条稀疏对角线

求非零对角线元素组成的矩阵B，以及对角线位置组成的向量d

主对角线以下，第三条对角线的元素是0，0，0，41，51

 主对角线的元素分别是11，21，31，42，52

主对角线以上，第三条对角线的元素是12，22，32，0，0

 

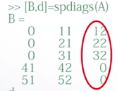
非0对角线元素组成的矩阵B，对角线位置组成的向量d

产生一个稀疏矩阵A

单位矩阵的稀疏矩阵

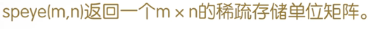
产生一个3阶稀疏存储的单位矩阵

例子

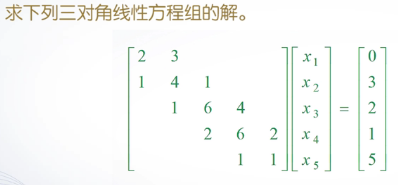
主对角线以下第一条，主对角线，主对角线上第一条的元素

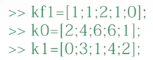
他们都成非0对角线元素矩阵B

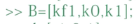
产生非0对角线元素位置向量d

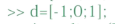
产生稀疏存储的稀疏矩阵A

建立方程右边的常数向量

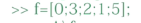
利用左除运算符求方程的解

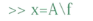
注意

为节省存储空间，加快运算速度，采用稀疏存储方式很有必要

 

转载于:https://www.cnblogs.com/fanglijiao/p/11103253.html