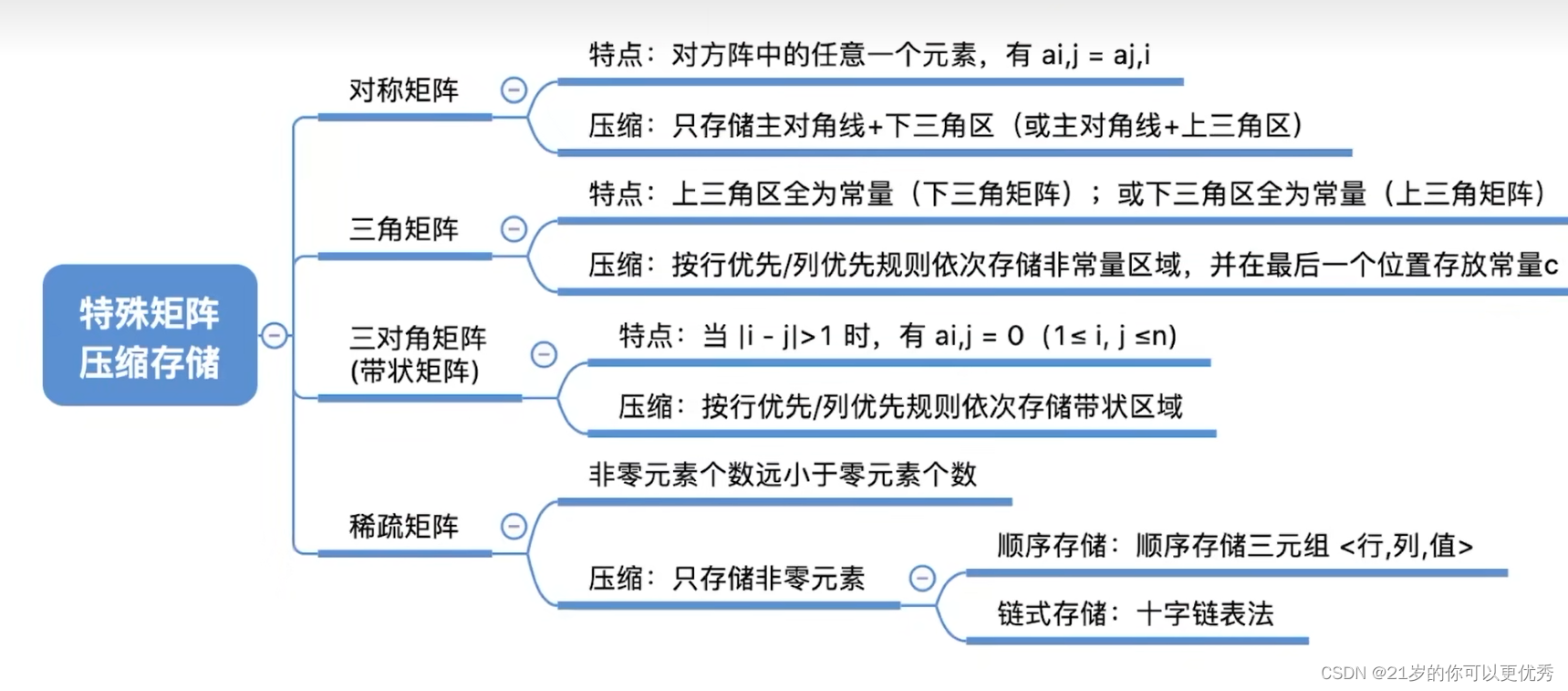
一、思维导图

二、特殊矩阵(由于一维数组和二维数组较为简单,就不写出来了)
1、对称矩阵
结构
存储策略:主对角线和下三角区,按照行优先存入一维数组
(1)数组大小:
n*(1+n)/2
(2)aij是第几个元素:
i(i-1)/2+j
如果是下标的话,就需要减一:i(i-1)/2+j-1
存储策略:主对角线和上三角区,按照行优先存入一维数组(由上面推导出来,不用算,因为由于对称矩阵的性质aij=aji)
(1)数组大小:
n*(1+n)/2
(2)aij是第几个元素:
j(j-1)/2+i
如果是下标的话,就需要减一:j(j-1)/2+i-1
存储策略:主对角线和下三角区,按照列优先存入一维数组
(1)数组大小:
n*(1+n)/2
(2)aij是第几个元素:
(n-j+2)(2n-j+2)/2+(i-j)+1
如果是下标的话,就需要减一:(n-j+2)(2n-j+2)/2+(i-j)
存储策略:主对角线和上三角区,按照列优先存入一维数组(由上面推导出来,不用算,因为由于对称矩阵的性质aij=aji)
(1)数组大小:
n*(1+n)/2
(2)aij是第几个元素:
(n-i+2)(2n-i+2)/2+(j-i)+1
如果是下标的话,就需要减一:(n-i+2)(2n-i+2)/2+(j-i)
2、三角矩阵
结构

存储策略:主对角线和下三角区,按照行优先存入一维数组,再将常量c存入一维数组末尾即可
(1)数组大小:
n(1+n)/2+1
(2)aij是第几个元素:
非常数c:i(i-1)/2+j 常数:n(1+n)/2+1
(3)aij的元素在数组的哪个下标:
非常数c:i(i-1)/2+j-1 常数:n(1+n)/2
3、三对角矩阵
结构
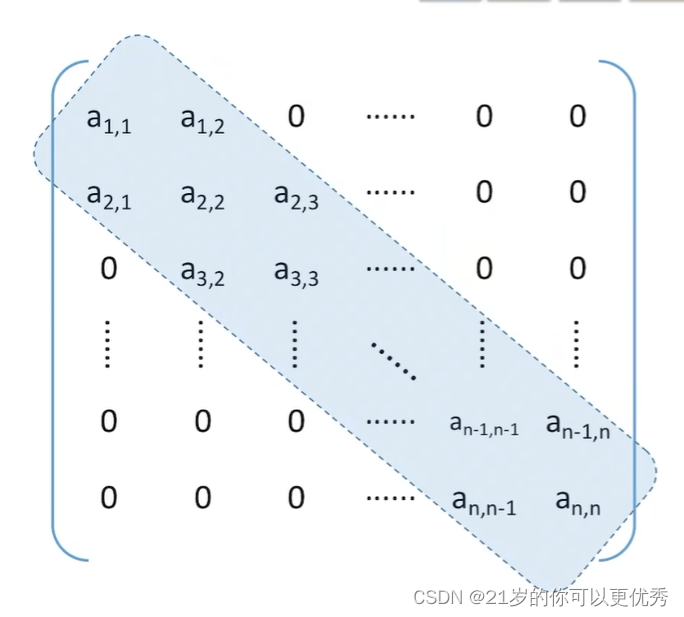
存储策略:只存储带状部分,按照行优先存储
(1)数组大小:
3n-2
(2)aij是第几个元素:
3(i-1)-1+(j-i)+2 ==> 2i+j-2
(3)aij是数组内的哪一个下标的元素
2i+j-3
(4)已知数组下标k,如何得到ij
第一种方法:

第二种方法:

小于等没截全:小于等于(这个是正确的)
由k下标=2i+j-3
再结合i=(k+2)/3(向上取整)或i=(k+1)/3+1(向下取整)
就可以完全算出j的值
4、稀疏矩阵
结构

顺序存储:三元组

链表存储:十字链表法(通过两个指针数组)
三、总结

























 2053
2053

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








