第二次作业

                                                                 

作业要求：

1. 1. 第一版本程序Prog1：
      + 给定一个数组，实现数组元素求和；具体要求：实现对一维数组(a[100])的所有元素相加运算。
      + 数据准备：a）数组长度：100；b）数组数据来源：实验数据A列：1~100，CSV 格式则填充 前100个数据.

   2. 第二版本程序Prog2：
      + 改写成一个函数（函数名称为ArraySum)，能实现任意长度数组所有元素求和；
      + 数据准备：a）数组长度：任意； b）数组数据来源：实验数据A列.

   3. 第三版本程序Prog3：
      + 将Prog2改写成能从文件中读取数据，实现任意长度数组，指定范围内元素相加。
      + 数据准备：a）数组长度：任意； b）数组数据来源：从文件中读取(A列). c)指定范围: (bottom, top)

                                                                     第一版程序

这道题目因为数据只有100个数，所以我用了比较笨的办法就是将这100个数全都输进去然后求和。源程序如下：

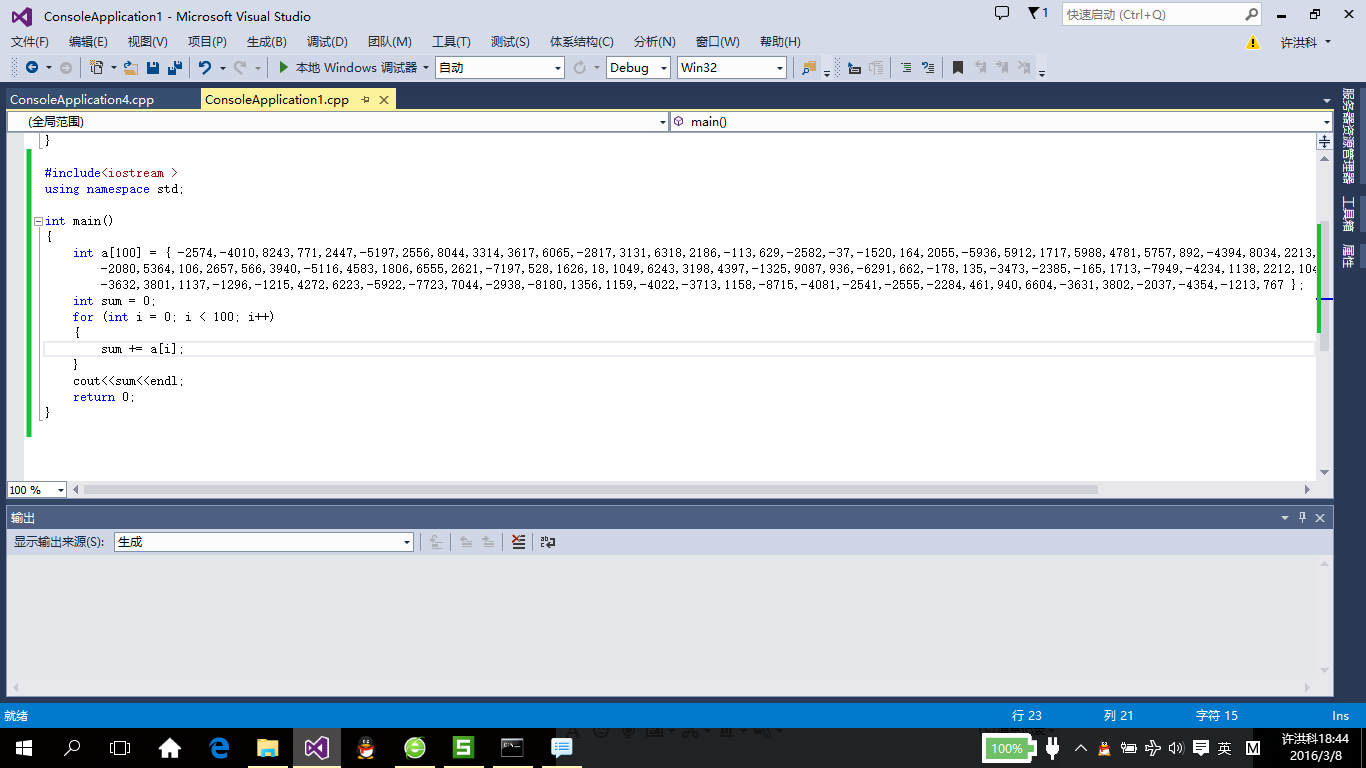
运行结果：

一开始在输入数据的时候，从EXCEL上复制的每个数据都占一行，把它们紧密排列起来也花费了不少的时间。

                                                                     第二版程序

源程序：

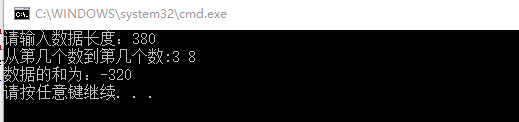
运行结果：

这道题采用了文件流的思想，但是在一开始调试的时候，一直都提示文件无法打开，试了好几遍都没有改观，后来我想到可能是文件的路径出现了问题，在将它复制到对应文件夹下后成功解决了问题。

 

                                                               第三版程序

源程序：

运行结果：

在第二题的基础上，这道题只需要再定义一组数据的范围。但是在调试过程中，发现输出结果只能显示出数据范围下限的值，后来经过研究，发现在数据范围的上限中没有添加“=”号，再次调试后输出结果正确。

 

个人总结：对于C++基础很薄弱的我来说，这次的作业还是有些困难的，数据流的部分自己掌握的也不是很好，在和同学讨论并且复习书本后，总算是完成了这次的作业，虽然说花了很多的时间，但是我觉得还是很值得的。并且将一个稍显复杂的程序分为三个阶段来完成也是很有趣味性的。

我的Github链接：https://github.com/Xuhongke

转载于:https://www.cnblogs.com/hongkexu/p/5255600.html