Eratosthenes筛法

最新推荐文章于 2024-02-07 22:08:35 发布

weixin_30872337

最新推荐文章于 2024-02-07 22:08:35 发布

阅读量115

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/-Wallace-/p/10552886.html

博客介绍了Eratosthenes筛法，它是一种素数筛法，能在近线性时间内制作1 - n的素数表。其思想是对正整数p筛除2p、3p、4p等，也可限定p为质数，算法复杂度为O(nloglogn)，还给出了模板题。

概况

Eratosthenes筛法是一个素数筛法，可以在近线性时间内制作出\(1-n\)的素数表。

\(\mathfrak{Eratosthenes}\)筛法

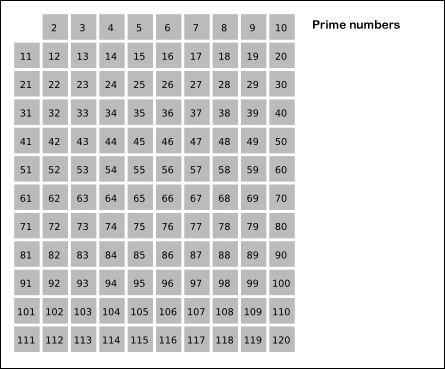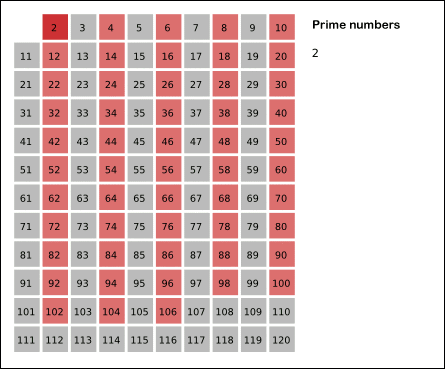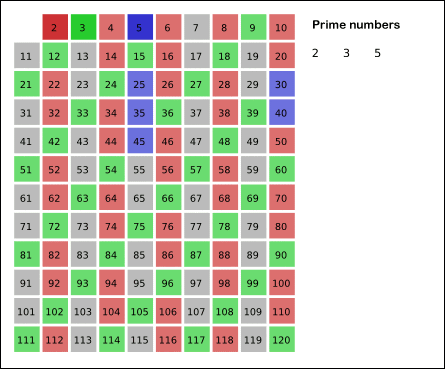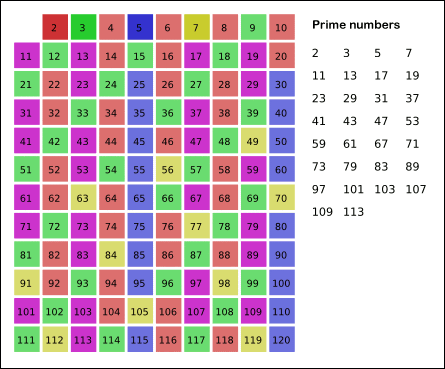
思想很简单。对于一个正整数\(p(p\in[1,n])\)，筛除\(2p,3p,4p,...\)，待将所有数处理完以后，剩下的就都是指质数了。

同时，我们还可以限定\(p\)为质数。

inline void Eratosthenes(int n)
{
    memset(isprime,0,sizeof(isprime));
    isprime[0]=isprime[1]=1;
    register int i,j;
    for(i=2;i*i<=n;i++)if(!isprime[i])
        for(j=i*i;j<=n;j+=i)
            isprime[j]=1;
    for(i=1;i<=n;i++)isprime[i]=(isprime[i])?0:1;
    return;
}

这个算法是\(O(nloglogn)\)的，可以基本满足需求。

模板题：Luogu P3383

转载于:https://www.cnblogs.com/-Wallace-/p/10552886.html