沉迷AC自动机无法自拔之：[BZOJ2434] [Noi2011] 阿狸的打字机

最新推荐文章于 2018-07-11 10:40:00 发布

weixin_30799995

最新推荐文章于 2018-07-11 10:40:00 发布

阅读量65

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/Hero-of-someone/p/7748478.html

本文详细介绍了使用AC自动机解决字符串匹配问题的具体方法，通过构建fail树并结合树链剖分与树状数组技巧，有效地处理了多个字符串的匹配查询。文章提供了完整的代码示例，适合有一定编程基础的学习者。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

如标题所言，我已经沉迷于AC自动机无法自拔了。。。
这又是一道AC自动的题，红红火火恍恍惚惚

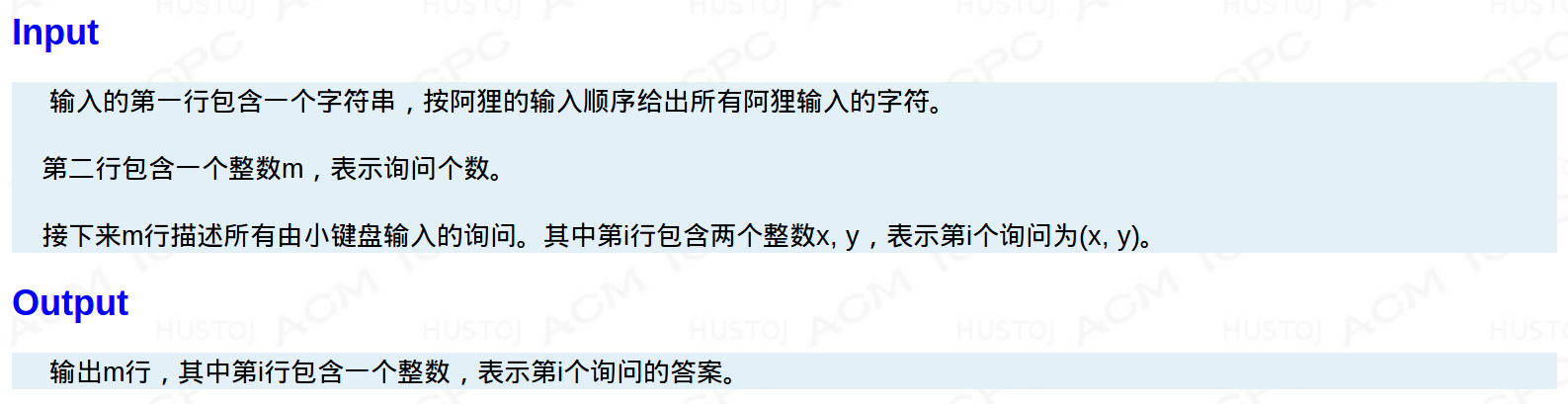
这题目做起来真舒服
简单概括一下：$AC$自动机$fail$树上树链剖分$+$树状数组
这种类型的题其实还蛮多的，比如这道：[HDU 4117] GRE Words
$
$
首先把$AC$自动机建出来，然后在所有子节点连一条由$fail$指向该点的边，这样一棵$fail$树就出来了。
题目问的是：求$x$在$y$中出现多少次，把问题放到$fail$树上来，就变成了：求从根到$y$的的节点中（这里指的是$dfs$序从根到$y$），有多少个在$x$的子树内
那么这个东西就很好求了，像普通的树链剖分题那样，用线段树就能维护，但是这道题只要查$root$到$y$，$bit$也适用且常数要更小些
具体做法：我们离线来做这道题，把$y$相同的询问放到一起来处理
考虑这样几个做法：

每次遇到$'P'$则统计答案当前点$y$的所有询问的答案；
遇到$'B'$则将当前点的$dfn$从$bit$（或线段树）中删除；
否则往下跳，并将该节点插入$bit$（或线段树）；

//made by Hero_of_Someone
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<vector>
#define N (100010)
using namespace std;

char s[N];

struct Trie{
  int size,root;
  int son[N][26],fail[N];
  int val[N],n,fa[N],ans[N];
  
  void init(){ size=1,root=0; }
  
  void insert(){
    int cur=root;
    for(int i=0;s[i];i++){
      if(s[i]=='P') val[++n]=cur;
      else if(s[i]=='B') cur=fa[cur];
      else{
    int id=s[i]-'a';
    if(!son[cur][id]) son[cur][id]=size++;
    fa[son[cur][id]]=cur,cur=son[cur][id];
      }
    }
  }

  int num,head[N],nxt[N],to[N];
  void add(int u,int v){
    nxt[++num]=head[u];to[num]=v;head[u]=num;
  }
  
  void build(){
    int que[N];
    int hd=0,tl=0;
    for(int i=0;i<26;i++)
      if(son[root][i]){
    que[tl++]=son[root][i];
    fail[son[root][i]]=root;
      }
      else son[root][i]=root;
  
    while(hd<tl){
      int cur=que[hd++];
      for(int i=0;i<26;i++){
    int Son=son[cur][i];
    if(Son){
      int f=fail[cur];
      while(f&&!son[f][i]) f=fail[f];
      fail[Son]=son[f][i];
      que[tl++]=Son;
    }
    else son[cur][i]=son[fail[cur]][i];
      }
    }
    for(int i=1;i<size;i++) add(fail[i],i);
  }
  
  int st[N],ed[N],tim,t[N];
  void dfs(int x){
    st[x]=++tim;
    for(int i=head[x];i;i=nxt[i]) dfs(to[i]);
    ed[x]=tim;
  }
  
  int lowbit(int x){return x&-x;}
  void up(int x,int val){for(;x<=tim;x+=lowbit(x))t[x]+=val;}
  int Q(int x){int ret=0;for(;x;x-=lowbit(x))ret+=t[x];return ret;}
  
  struct node{ int x,id; }; vector<node>p[N];
  
  void Ans(){
    int m; scanf("%d",&m);
    for(int i=1;i<=m;i++){
      int x,y; scanf("%d%d",&x,&y);
      p[val[y]].push_back((node){x,i});
    }
    int x=0;
    for(int i=0;s[i];i++){
      if(s[i]=='P')
    for(int j=0,l=p[x].size();j<l;j++){
      int X=p[x][j].x,ID=p[x][j].id;
      ans[ID]=Q(ed[val[X]])-Q(st[val[X]]-1);
    }
      else if(s[i]=='B') up(st[x],-1),x=fa[x];
      else x=son[x][s[i]-'a'],up(st[x],1);
    }
    for(int i=1;i<=m;i++) printf("%d\n",ans[i]);
  }
  
}AC;

void init(){ AC.init(); scanf("%s",s); AC.insert(); AC.build(); }

void work(){ AC.dfs(0); AC.Ans(); }

int main(){ init(); work(); return 0; }

转载于:https://www.cnblogs.com/Hero-of-someone/p/7748478.html