用verilog实现log2的一种方法

在博文《Computing the Logarithm Base 2》和《Getting the Log Base 2 Algorithm to Synthesize》中，作者把log2(x)的运算分成了整数部分和小数部分。其中，整数部分通过一个递归模块来实现（这个我是第一次看到，原来还能这么用），小数部分通过查找表来实现。

在网上找log2的verilog实现基本都是下面的function：

function integer log2;
  input integer value;
  begin
    value = value-1;
    for (log2=0; value>0; log2=log2+1)
      value = value>>1;
  end
endfunction

这个是无法综合实现的。仔细分析一下可以发现这是log2(x)运算的整数部分，等效于去找value的最左边第一个1出现的位置。上面博文中的作者用递归算法实现，正常还可以用二分法实现。

综上所述，我使用的方法同样是把log2(x)的运算分成整数部分和小数部分。其中，整数部分通过二分法实现来实现，小数部分通过查找表来实现。

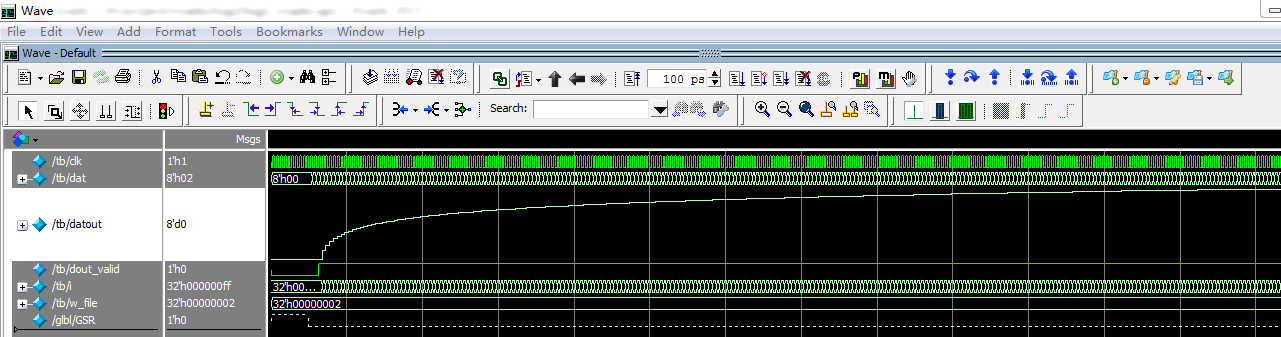
综合后的时序仿真结果如下图所示：

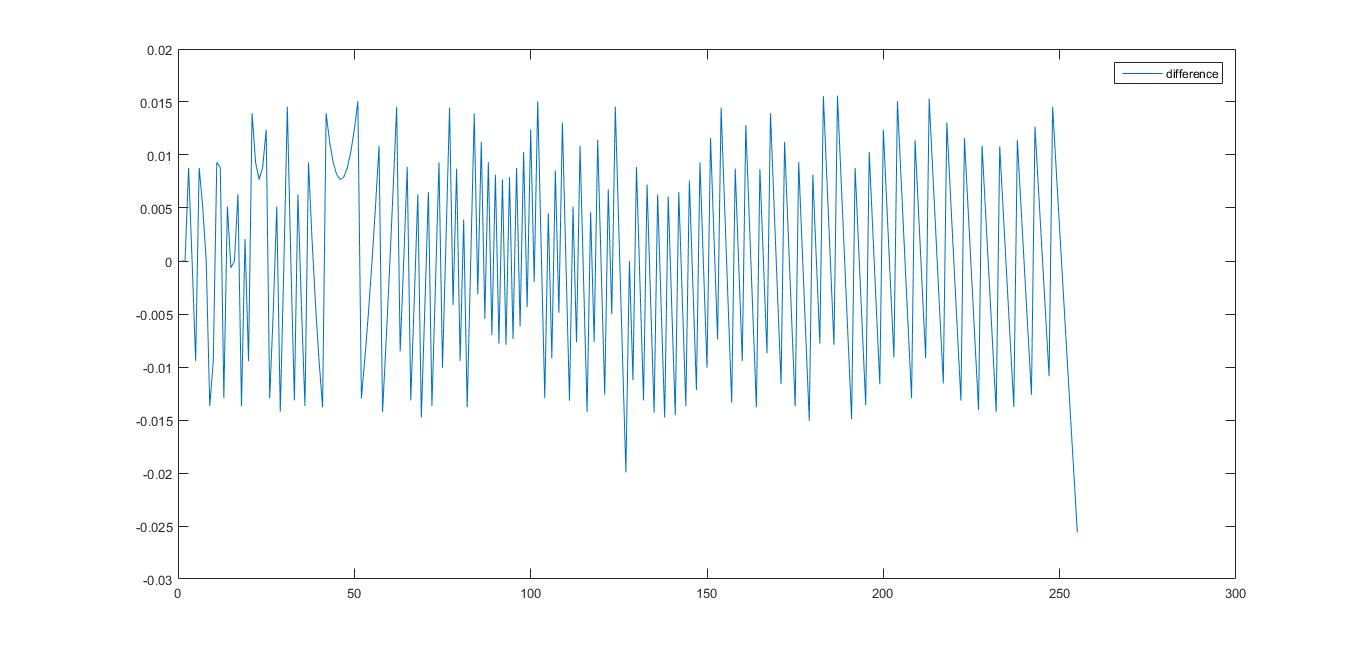
使用matlab验证结果，将仿真得到的结果和实际的结果相减，如下图所示。可以看到最大偏差不超过0.03。

Implementation后的实际测试结果我没有试过，估计问题不大。我的输入和输出都是8位数，输出整数部分为3位（因为log2(255)=7.9944<8，所以3位够了），小数部分为8-3=5位。如果你需要提高精度，可以增大小数位数，相应的查找表需要修改。

工程下载地址，包括全部仿真文件和matlab文件。转载请注明出处。

转载于:https://www.cnblogs.com/fimwest/p/8052468.html