考虑这种情况:
倘若我们使用Hard-Margin SVM,不容许一点点的错误,就会得到右边的结果。很显然,左边的结果更合理,所以在实际情况中,我们使用能够接纳一定错误(容忍噪声)的SVM,即:soft-margin SVM。
合并两个条件,得:
这样做有几个问题:
一是我们的目标函数不再是线性的,所以不能使用QP;第二是我们对大的误差和小的误差一视同仁。
所以我们将∞更换为ε:
(这一点也是一个疑问:ε对于每一个数据都不同,甚至也成为一个目标变量。不是很容易理解)
现在soft-margin SVM的形式已经阐明,如何来解?
1.根据之前我们在hard-margin SVM中推导过的求解对偶问题的过程,可以得到如下结果,同时还有KKT condition中的primal-innner optimal(complementary slackness)。
求解:
这里的问题是b如何求得?根据之前的primal-innner optimal 条件:
至此,soft-margin SVM的求解过程结束。
之前hard-margin我们将所有的数据点根据α的值,分为支持向量和一般向量。
现在soft-margin中,α有三种情况,可以分成三类:
对于高斯核函数,如何选择适当的C和γ?
可以使用validation。同时也可以使用#SV,因为:
使用两者进行选择的区别如下:




 本文深入探讨了软边界支持向量机(SVM)的原理及求解过程,包括如何通过引入ε值处理噪声数据,以及在实际应用中选择合适的C和γ参数的方法。同时,阐述了软边界SVM与硬边界SVM的区别,并通过实例说明了软边界SVM在解决噪声数据集问题上的优势。
本文深入探讨了软边界支持向量机(SVM)的原理及求解过程,包括如何通过引入ε值处理噪声数据,以及在实际应用中选择合适的C和γ参数的方法。同时,阐述了软边界SVM与硬边界SVM的区别,并通过实例说明了软边界SVM在解决噪声数据集问题上的优势。


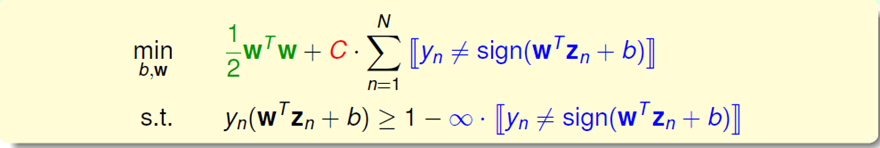





























 471
471

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








