LOJ #6268. 分拆数

最新推荐文章于 2020-03-28 18:56:10 发布

weixin_30715523

最新推荐文章于 2020-03-28 18:56:10 发布

阅读量185

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/JYYHH/p/8954965.html

本文提出了一种解决背包问题的有效方法，通过将问题分解为两部分：小于等于sqrt(n)的物品暴力填充与大于sqrt(n)的物品使用动态规划进行处理，并最终利用NTT进行合并，以达到高效的解决方案。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

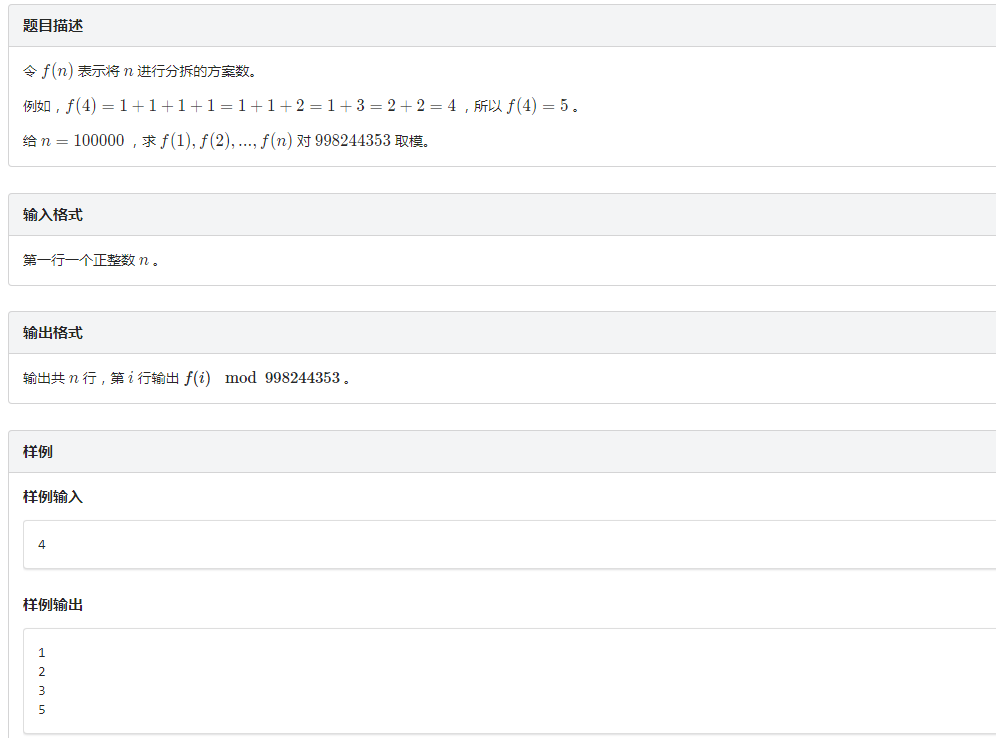
可以先将问题建模为：物品大小为1~inf 且每件物品数量无限的背包选体积为1~n的方案数。

显然物品体积只有1~n有用，我们不妨把体积1~sqrt(n) 的物品先暴力插入到背包中，设这一部分最后体积i的方案数是 A[i] 。

考虑体积>sqrt(n)的物品怎么计算方案，可以发现这样的物品最多只能有sqrt(n)件。

这有什么用呢？当然是dp用啊！设f[i][j] 为选了i件>sqrt(n)的物品，且总体积是j的方案数，显然第一维只有sqrt(n)，直接转移做就行了，设这一部分最后体积i的方案数是B[i]。

不过还有一点很恶心：我们还要合并 A[] 与 B[]。

也没啥，写个NTT就好了hhhh

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=100005,root=3,ha=998244353,inv=ha/3+1,Base=333;
inline int add(int x,int y){ x+=y; return x>=ha?x-ha:x;}
inline void ADD(int &x,int y){ x+=y; if(x>=ha) x-=ha;}
void W(int x){ if(x>=10) W(x/10); putchar(x%10+'0');}
int A[maxn*4],F[Base+5][maxn],B[maxn*4],r[maxn*4],n,l,S,N,INV;
inline int ksm(int x,int y){ int an=1; for(;y;y>>=1,x=x*(ll)x%ha) if(y&1) an=an*(ll)x%ha; return an;}

inline void dp(){
	A[0]=1;
	for(int i=1;i<Base;i++)
	    for(int j=i;j<=n;j++) ADD(A[j],A[j-i]);
	    
	F[0][0]=1,S=maxn/Base+1,F[1][Base]=1;
	for(int i=1;i<S;i++)
	    for(int j=0;j<=n;j++) if(F[i][j]){
	    	if(j+i<=n) ADD(F[i][j+i],F[i][j]);
	    	if(j+Base<=n) ADD(F[i+1][j+Base],F[i][j]);
	    	ADD(B[j],F[i][j]);
		}
	ADD(B[0],1);
}

inline void NTT(int *c,int f){
	for(int i=0;i<N;i++) if(i<r[i]) swap(c[i],c[r[i]]);
	
	for(int i=1;i<N;i<<=1){
		int omega=ksm((f==1?root:inv),(ha-1)/(i<<1));
		for(int P=i<<1,j=0;j<N;j+=P){
			int now=1;
			for(int k=0;k<i;k++,now=now*(ll)omega%ha){
				int x=c[j+k],y=c[j+k+i]*(ll)now%ha;
				c[j+k]=add(x,y);
				c[j+k+i]=add(x,ha-y);
			}
		}
	}
	
	if(f==-1) for(int i=0;i<N;i++) c[i]=c[i]*(ll)INV%ha;
}

int main(){
	scanf("%d",&n),dp();
	
	for(N=1;N<=(n<<1);N<<=1) l++;
	for(int i=0;i<N;i++) r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));
	NTT(A,1),NTT(B,1);
	for(int i=0;i<N;i++) A[i]=A[i]*(ll)B[i]%ha;
	INV=ksm(N,ha-2),NTT(A,-1);
	
	for(int i=1;i<=n;i++) W(A[i]),puts("");
	return 0;
}

转载于:https://www.cnblogs.com/JYYHH/p/8954965.html