【数值优化】基础

 “数值”优化：设置算法时，要考虑舍入误差。

数值优化问题分类：

• 无约束优化  VS 约束优化
• 线性规划。目标函数和约束函数都是线性的
• 二次规划。目标函数为二次的，约束函数为线性。
• 凸优化。目标函数为凸的，约束函数为线性的。

局部解 VS 全局解

连续   VS  离散

确定  VS  随机

无约束优化问题基础

解的一阶必要条件：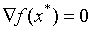

解的二阶必要条件：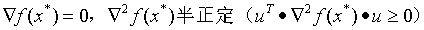

解的二阶充分条件：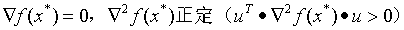

迭代算法（如何构造下一个迭代点）、终止条件

一阶、二阶、直接算法

直接算法无需使用导数，一阶算法需要使用一阶导数，二阶算法需要用到二阶导数。

算法的收敛性：

全局收敛的算法：

局部收敛的算法：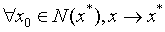

 算法收敛速度

线性收敛：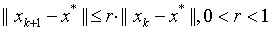

超线性收敛：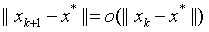

二次收敛：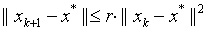

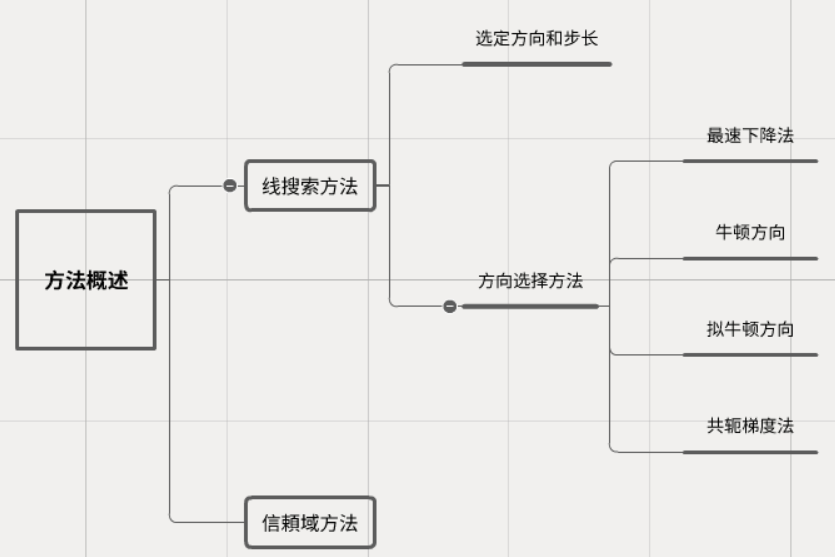
方法概述

 

转载于:https://www.cnblogs.com/larry-xia/p/9310854.html