1 //并查集数据结构主要用于求连通子图,最小生成树的kruskal算法和最近公共祖先(Least Common Ancestors,LCA,等价类问题)
2 //前提条件:任意两个集合不能相交.
3 // (1) 不相交集合的并
4 // (2) 查找某个集合元素所属的集合
5
6 #include<stdio.h>
7 #define MAX_ELEMENTS 100
8
9 int parent[MAX_ELEMENTS] ;
10
11 /*
12 *创建集合,并对集合初始化
13 * */
14 void MakeSet()
15 {
16 int i;
17 // for( i=0 ;i<10 ;i++)
18 // parent[i]=-1; //从而表示初始化时每个结点都是根节点
19 //用于测试
20 parent[0]=-4;
21 parent[1]=4;
22 parent[2]=-3;
23 parent[3]=2;
24 parent[4]=-3;
25 parent[5]=2;
26 parent[6]=parent[7]=parent[8]=0;
27 parent[9]=4;
28 }
29 /*
30 *递归
31 * */
32 int Find1Recursive(int i)
33 {
34 if( parent[i]>=0)
35 Find1Recursive( parent[i] );
36 else
37 return i;
38 }
39
40 /*
41 *非递归
42 * */
43 int Find1(int i)
44 {
45 while( parent[i]>=0 )
46 {
47 i=parent[i];
48 }
49 return i;
50 }
51 /*
52 *把第一棵树作为第二棵树的子树
53 * */
54 void Union1(int i ,int j) //刚开始设计的时候暂时没有考虑合并的树的扁平问题,所以合并后根节点的parent[root]没有发生变化
55 {
56 int pID=Find1(i);
57 int qID=Find1(j);
58 if(pID!=qID)
59 parent[pID]=qID;
60 }
61
62 /*
63 *
64 *对Find1的改进,由于Union操作用到Find操作,所以Find操作的效率至关重要,我们可以通过路径压缩的思想,降低树的高度
65 *查找结点i时,从i到根节点的所有结点都使其指向根节点
66 * */
67 int Find2(int i)
68 {
69 int p=i;
70 while( parent[i]>=0 )
71 i=parent[i]; //此时退出循环找到了根节点i
72 while(parent[p]>=0) //使路径上的结点都指向根节点
73 {
74 int t=parent[p];
75 parent[p]=i;
76 p=t;
77 }
78 return i;
79 }
80
81 /*
82 *对Union1的改进,把较小结点数的树作为较大树的子树,从而防止树的高度退化为单链表
83 * */
84 void Union2(int i ,int j)
85 {
86 int pID=Find2(i);
87 int qID=Find2(j);
88 if(pID==qID)
89 return ;
90 else
91 {
92 if(parent[pID] < parent[qID]) //如 -9 ,-5
93 {
94 parent[pID]=parent[pID]+parent[qID];
95 parent[qID]=pID;
96 }
97
98 else
99 {
100 parent[qID]=parent[pID]+parent[qID];
101 parent[pID]=qID;
102
103 }
104 }
105 }
106
107 void PrintSet()
108 {
109 int i;
110 for( i=0 ;i<10 ;i++)
111 printf("%d ",parent[i]);
112 printf("\n");
113 }
114
115 int main()
116 {
117 MakeSet();
118 printf("the original set :\n");
119 PrintSet();
120 int i=7;
121 int s=Find1Recursive(i);
122 printf("\n%d belongs to Set %d\n",i,s);
123 s=Find1(i) ;
124 printf("\n%d belongs to Set %d\n",i,s);
125 Union1(1,6);
126 printf("after the Find1 and Union1 set :\n");
127 PrintSet();
128
129
130 printf("\n*************\n");
131 MakeSet();
132 printf("the original set :\n");
133 PrintSet();
134 i=5;
135 s=Find2(i);
136 printf("\n%d belongs to Set %d\n",i,s);
137 i=9;
138 s=Find2(i);
139 printf("\n%d belongs to Set %d\n",i,s);
140
141 Union2(1,6);
142 printf("after the Find2 and Union2 set :\n");
143 PrintSet();
144
145 printf("%d 所属集合的元素的个数:%d\n",i,- parent[ Find1(i) ] );
146 return 1;
147 }


 View Code
View Code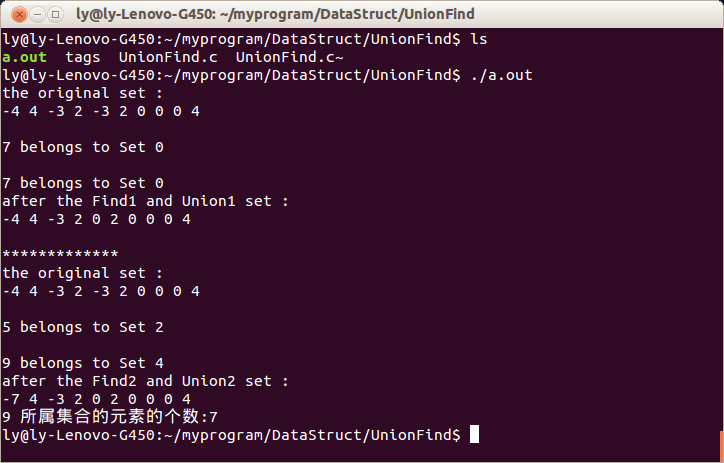







 本文详细介绍了并查集数据结构的基本概念、实现方法及应用场景。包括如何通过递归和非递归方式查找集合,以及如何进行集合的合并。特别讨论了通过路径压缩和按秩合并来优化并查集的操作效率。
本文详细介绍了并查集数据结构的基本概念、实现方法及应用场景。包括如何通过递归和非递归方式查找集合,以及如何进行集合的合并。特别讨论了通过路径压缩和按秩合并来优化并查集的操作效率。
















 1688
1688

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








