迷宫 II 广搜

最新推荐文章于 2021-08-12 09:16:45 发布

weixin_30587927

最新推荐文章于 2021-08-12 09:16:45 发布

阅读量98

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/gshdyjz/p/7687113.html

本文介绍了一种解决特殊六边形迷宫最短路径问题的算法实现，该迷宫由多个三角形单元组成。文章详细展示了如何使用广度优先搜索（BFS）来寻找从起点到终点的最少经过点数，并给出了完整的C++代码实现。

【问题描述】
山山厌倦了普通的迷宫,他准备挑战奇妙的迷宫 II。迷宫 II 是由若干三角形拼成的六边形
(见样例)
,其中有些点可以通过,有些点不能通过。你需要计算从起点走到终点至少要经
过多少点(不包括起点终点)
。

【输入格式】
第一行,一个整数 n,表示地图边长
接下来若干行字符串,表示一个地图。其中.表示可以经过的点,+表示不能经过的点,s 和
t 表示起点与终点。点与点之间由一个空格隔开。一行开头有一些用来保持格式的空格(见
样例)
。数据保证只有一对 s 与 t。
【输出格式】
一行一个整数 L,表示至少要经过的点数。若无解,输出-1

【样例输入】
3
. . .
. s . .
. . + . .
. . t .
. . .

【样例输出】
2

【样例解释】

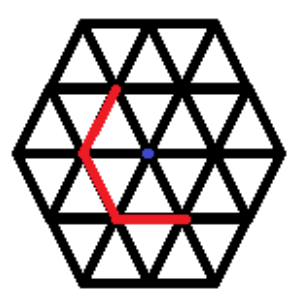
【数据范围】
100%的数据保证 n ≤ 10

这道题主要就是搜索的时候，注意要考虑情况搜六个方向。

代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>

#define ll long long
#define il inline
#define db double

using namespace std;

int n;

int src[2],des[2];

int limit[45];

int t[1000045][3];

int head,tail=1;

int dist[5]={0,1,0,-1,0};

bool vis[45][45];

il void check(int x,int y,int c)
{
	if(x<1||y<1||x>2*n-1||y>limit[x]||vis[x][y])
		return;
	vis[x][y]=1;
	t[tail][0]=x;
	t[tail][1]=y;
	t[tail++][2]=c+1;
	if(x==des[0]&&y==des[1])
		{
			printf("%d\n",c);
			exit(0);
		}
}

il void bfs()
{
	t[0][0]=src[0];
	t[0][1]=src[1];
	vis[src[0]][src[1]]=1;

	int a,b,c,x,y;

	while(head!=tail)
		{
			a=t[head][0],b=t[head][1],c=t[head++][2];
			for(int i=0;i<4;i++)
				{
					x=a+dist[i],y=b+dist[i+1];
					check(x,y,c);
				}
			if(a>n)
				{
					x=a-1,y=b+1;
					check(x,y,c);
					x=a+1,y=b-1;
					check(x,y,c);
				}
			else if(a<n)
				{
					x=a-1,y=b-1;
					check(x,y,c);
					x=a+1,y=b+1;
					check(x,y,c);
				}
			else if(a==n)
				{
					x=a-1,y=b-1;
					check(x,y,c);
					x=a+1,y=b-1;
					check(x,y,c);
				}
		}
}

int main()
{
	freopen("maze2.in","r",stdin);
	freopen("maze2.out","w",stdout);

	cin>>n;
    
	char ch;

	limit[0]=n-1;
	for(int i=1;i<2*n;i++)
		{
			if(i<=n)
				limit[i]=limit[i-1]+1;
			else
				limit[i]=limit[i-1]-1;
			for(int j=1;j<=limit[i];j++)
				{
					cin>>ch;
					if(ch=='+')
						vis[i][j]=1;
					if(ch=='s')
						src[0]=i,src[1]=j;
					if(ch=='t')
						des[0]=i,des[1]=j;
				}
		}

	bfs();

	return 0;
}

转载于:https://www.cnblogs.com/gshdyjz/p/7687113.html