004-1-代价函数与激活函数

最新推荐文章于 2024-09-10 16:49:49 发布

转载最新推荐文章于 2024-09-10 16:49:49 发布 · 142 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/Mjerry/p/9828075.html

文章标签：

#人工智能

本文通过使用TensorFlow框架，介绍了如何将交叉熵作为损失函数应用于MNIST手写数字识别任务中。通过对比二次代价函数，展示了交叉熵在分类问题上的优势。实验结果显示，在相同的训练条件下，使用交叉熵函数可以达到更高的测试准确性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

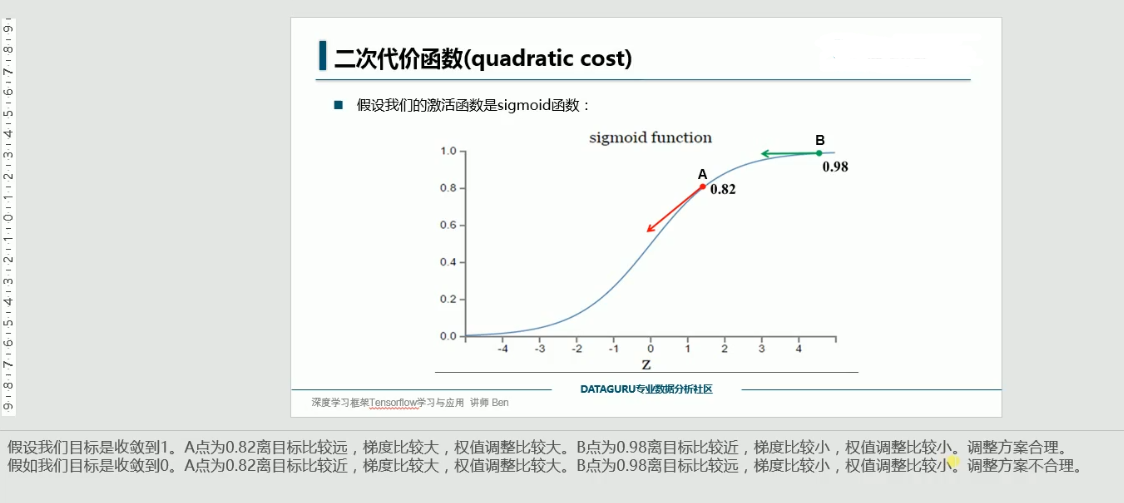
同样对于上一课的例子，将二次代价函数换成交叉熵函数

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
#载入数据
mnist = input_data.read_data_sets("MNIST_data",one_hot = True)

#定义每个批次的大小
batch_size = 100
#计算一共有多少个批次
n_batch = mnist.train.num_examples//batch_size

#定义2个placeholder
x = tf.placeholder(tf.float32,[None,784])
y = tf.placeholder(tf.float32,[None,10])

#创建一个简单的神经网络：
W = tf.Variable(tf.zeros([784,10]))
b = tf.Variable(tf.zeros([10]))
prediction = tf.nn.softmax(tf.matmul(x,W)+b)

#二次代价函数：
# loss = tf.reduce_mean(tf.square(y-prediction))
#对数似然函数
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(labels= y,
                                                  logits= prediction)) 

#梯度下降
train_step = tf.train.GradientDescentOptimizer(0.2).minimize(loss)

#初始化变量
init = tf.global_variables_initializer()

#求准确率
#比较预测值最大标签位置与真实值最大标签位置是否相等
correct_prediction = tf.equal(tf.argmax(y,1),tf.argmax(prediction,1))
#求准去率
accuracy = tf.reduce_mean(tf.cast(correct_prediction,tf.float32))

with tf.Session() as sess:
    sess.run(init)
    for epoch in range(21):
        for batch in range(n_batch):
            batch_xs,batch_ys = mnist.train.next_batch(batch_size)
            sess.run(train_step,feed_dict = {x:batch_xs,y:batch_ys})
        acc = sess.run(accuracy,feed_dict ={x:mnist.test.images,
                                            y:mnist.test.labels})
        print("Iter"+str(epoch+1)+",Testing accuracy"+str(acc))

Extracting MNIST_data\train-images-idx3-ubyte.gz
Extracting MNIST_data\train-labels-idx1-ubyte.gz
Extracting MNIST_data\t10k-images-idx3-ubyte.gz
Extracting MNIST_data\t10k-labels-idx1-ubyte.gz
Iter1,Testing accuracy0.8339
Iter2,Testing accuracy0.895
Iter3,Testing accuracy0.9011
Iter4,Testing accuracy0.9053
Iter5,Testing accuracy0.908
Iter6,Testing accuracy0.9117
Iter7,Testing accuracy0.9123
Iter8,Testing accuracy0.913
Iter9,Testing accuracy0.9147
Iter10,Testing accuracy0.9166
Iter11,Testing accuracy0.9178
Iter12,Testing accuracy0.9189
Iter13,Testing accuracy0.9183
Iter14,Testing accuracy0.9178
Iter15,Testing accuracy0.9198
Iter16,Testing accuracy0.92
Iter17,Testing accuracy0.9206
Iter18,Testing accuracy0.9206
Iter19,Testing accuracy0.9208
Iter20,Testing accuracy0.9209
Iter21,Testing accuracy0.9212

转载于:https://www.cnblogs.com/Mjerry/p/9828075.html