RMQ((Range Minimum/Maximum Query))ST算法

给定一个数组，求出给定区间[l,r]中元素的最大值或最小值或者最值的索引。

一看到这个题目，简单，看我暴力出奇迹。暴力当然是可行的。但是时间复杂度很高(O(n^2))。线段树，树状数组也可以解决这个问题，复杂度(O(nlogn))的预处理,最终查询为O(次数*logn)。

而今天用ST(Sparse_Tabl)算法，也是O(nlogn)的预处理，但是是单次查询为O(1)，挺高效的。

我们现在给定一组数据 n==9,元素为2,4,6,8,9,1,2,3,4。一个二维数组f[MAX][MAX];假设我们求区间最大值的问题。

f[i][j]的定义是这样的，维护从当前i的位置开始，共2^j个元素中的最大值。

如果f[i][0]则表示从自身到自身(2^0==1)的元素的最大值。f[i][1]表示从自身到下一个元素(2^1==2)中最大的那个。依次类推。

但是，这个二维数组也是有范围的。总共就n个元素，所以j的最大值为log2(n),而i的范围则是受j的范围影响的。即j每次跨度越小，i的范围就越大，如果j的跨度较大，i的范围就小。

另外，f数组的计算过程如下

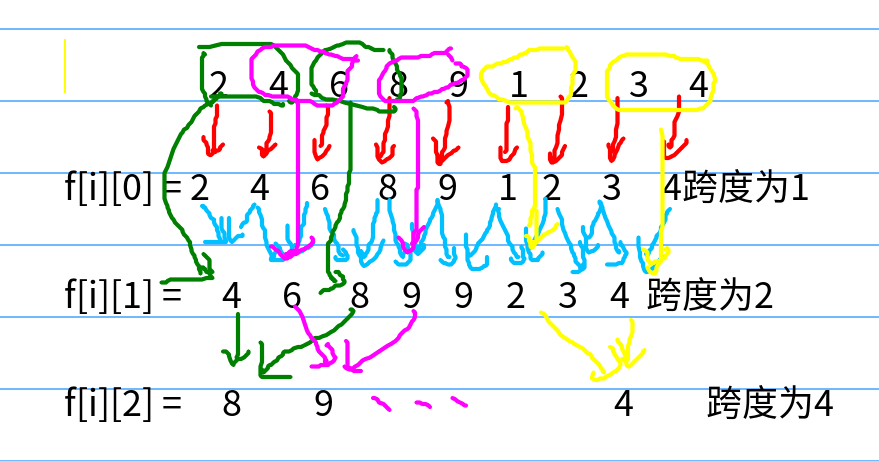
f[1][0]就是数组本身，f[1][1]就是自己和下一个元素的最大值，f[1][2]是自己和后三个元素中的最大值(共2^2==4个)，而这个不需要重新去比较4个，而是在f[1][1](有前两个和后两个的最大值)的基础上，比较2个就好了。

这样，每一个元素往后的2^k次方的中的最大值就保存下来了。

那么，如何计算给定区间[i,j]中的最大值呢

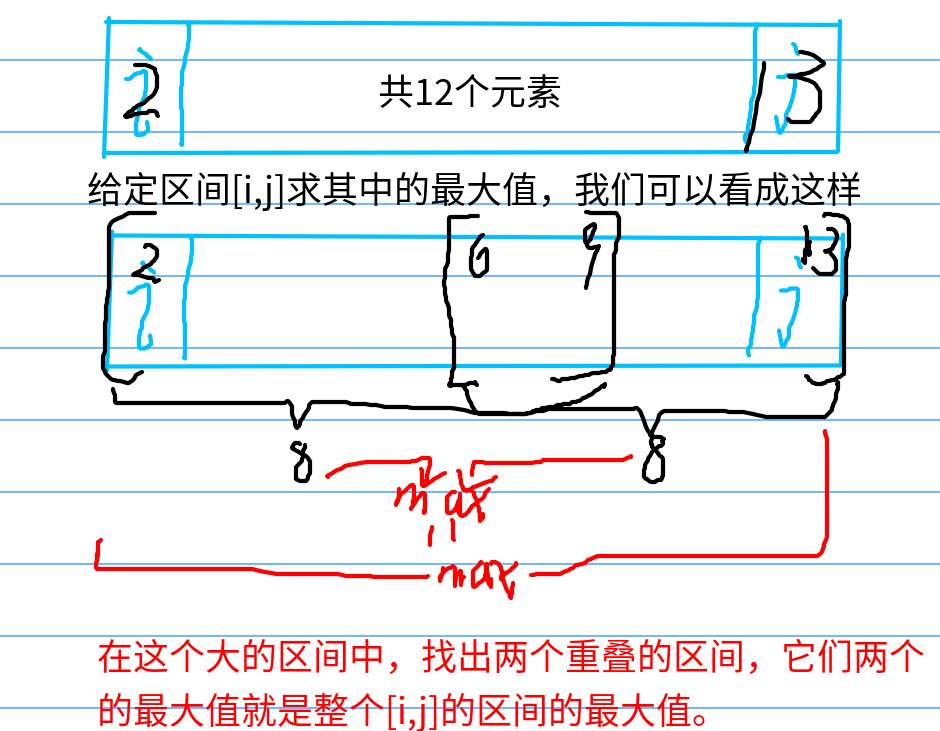
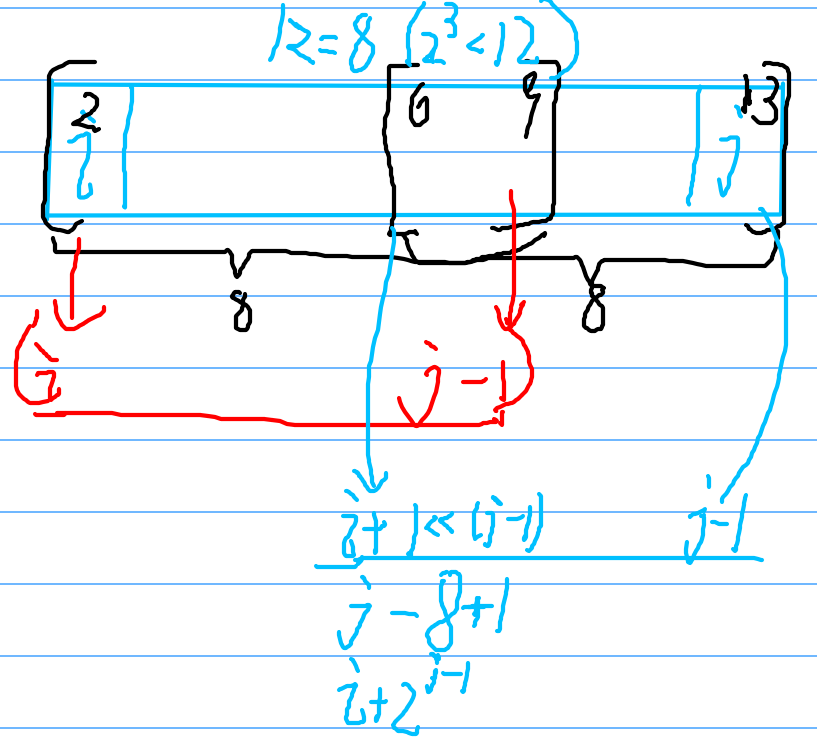
上图中，根据范围分别算出两个子区间的f[i][j]中的i和j，即f[i][j-1]和f[i+1<<(j-1)][j-1]，子区间范围是k==8。

那么，两个子区间的范围k怎么确定呢？很简单，根据i到j的范围，k<log2(j-i+1)，即不超过要求范围[i,j]的2^k的最大的那个k。这样，无论如何，两个子区间都能完全覆盖整个所求区间，重叠了也不会影响结果。

图中找出2^3==8< 12,子区间是重叠的，如果[i,j]是4,那么2,2的子区间就行，这个则不重叠。

这样，就能得到问题的解。这个查询时间复杂度是O(1)的，上述计算在预处理中即可完成。

 1 for(int i = 1;i <= n; i++)
 2     {
 3         f[i][0] = arr[i];//存放最大，从i开始，长度为2^0距离的最大值为自己
 4         v[i][0] = arr[i];//存放最小
 5     }
 6     for(int j = 1; (1<<j)<=n ;j++)//j<=m
 7     {
 8         for(int i = 1;i+(1<<j)-1 <=n ;i++)//i的范围受j的跨度的影响
 9         {    
10             v[i][j] = min( v[i][j-1] , v[i+(1<<(j-1))][j-1]);
11             f[i][j] = max( f[i][j-1] , f[i+(1<<(j-1))][j-1]);
12         }
13     }

View Code

这个题目可以练练手，纯RMQ(线段树当然也ok)---- 传送门

转载于:https://www.cnblogs.com/ygsworld/p/11144243.html