已知点和线, 求垂足

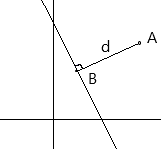
1. 已知点 \(A(x_1, y_1)\), 现有一条直线 \(l\): \(ax+by+c=0\), 直线 \(l\) 到\(A\) 的举例为 \(d\), 点 \(A\) 到直线 \(l\) 的垂足点记为 \(B\), 求 \(B\) 的坐标.

• 解答

  已知直线的表达式, 可知直线上的一个垂线量为: \((a,b)\), 记 \(B\) 的坐标表示为 \((x_2,y_2)\), 那么向量 \(\overrightarrow{BA} = (x_1 - x_2, y_1 - y_2)\), \(d(A,B)=d\), 所以, \(\frac{(a,b) \cdot d}{\left\|(a,b)\right\|_2} = (x_1 - x_2, y_1 - y_2)\), 所以 \(B\) 表示为:
  \[ (x_2,y_2)=(x_1,y_2) - \frac{(a,b) \cdot d}{\left\|(a,b)\right\|_2}, \]
  推向多项式表示, 超平面表示为 \(\omega x + b = 0\), 点 \(A\) 坐标表示为 \(x_0\), \(A\) 到 \(B\) 的距离表示为 \(\gamma\), 那么 \(B\) 表示为:
  \[ x_1 = x_0 - \gamma \cdot \frac{\omega}{\left\| \omega \right\|_2} \]

转载于:https://www.cnblogs.com/ouyxy/p/10628678.html