天鹅会面

最新推荐文章于 2024-11-12 11:42:32 发布

weixin_30470857

最新推荐文章于 2024-11-12 11:42:32 发布

阅读量72

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/A-LEAF/p/7295746.html

天鹅会面

【题目描述】

两头白天鹅生活在一个部分湖面结了冰的湖泊中，湖面的形状为一个长方形，并且被分割成R行C列的小方格，某些方格中结了冰，这样的方格称之为冰格，其余的方格称之为水格。冬天过去了，湖面上的冰渐渐开始溶解了，每一天与水相邻的冰格就将消融而转化为水格。所谓两个方格相邻是指它们在水平或垂直方向有公共边，两个呈对角的方格是不相邻的，下图给出样例数据的演化过程。

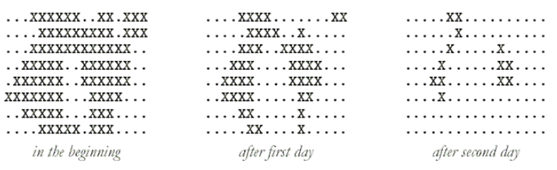
白天鹅只能在水中沿水平或垂直方向游动，写一个程序判断多少天后两只白天鹅才能够相会。

【输入格式】

输入文件第一行包含两个用空格隔开的整数R和C，其中1 ≤ R, C ≤ 1500，接下来的R行每行包含C个字符，描述湖面的初始状态，‘·’表示水格，‘ X’表示冰格，‘ L’表示一只白天鹅。

【输出格式】

输出文件仅一行包含一个整数表示两只白天鹅等到相邻那一天所需的天数。

【输入样例】

8 17

...XXXXXX..XX.XXX

....XXXXXXXXX.XXX

...XXXXXXXXXXXX..

..XXXXX.LXXXXXX..

.XXXXXX..XXXXXX..

XXXXXXX...XXXX...

..XXXXX...XXX....

....XXXXX.XXXL...

【输出样例】

Hint

30%数据1 ≤ R《400.1 ≤ C《300

100%其中1 ≤ R, C ≤ 1500

solution

一想就是bfs，但是考试的时候一想能暴力拿点分，就直接打了最暴力的暴力就是按照时间模拟

正解是：

先bfs一遍求出每个点能融化最早的天数

然后从某一个天鹅开始bfs，寻找到另一只天鹅所有路径上冰块最晚化的最大值的最小值(有点绕)

  1 #include<cstdio>
  2 #include<cstring>
  3 #include<iostream>
  4 #define mem(a,b) memset(a,b,sizeof(a))
  5 using namespace std;
  6 const int N=1506;
  7 const int INF=(1<<31)-1;
  8 inline int maxn(int a,int b){return a>b?a:b;}
  9 int read()
 10 {
 11     char q=getchar();
 12     while(q!='.'&&q!='X'&&q!='L')q=getchar();
 13     if(q=='.')return 1;
 14     if(q=='X')return 0;
 15     if(q=='L')return 2;
 16 }
 17 struct son
 18 {
 19     int x,y;
 20 }dui[20000001],pos[2];
 21 int he,en,hhh=-1;
 22 
 23 int n,m;
 24 int a[N][N],d[N][N];
 25 int vis[N][N],quick[N][N];
 26 
 27 void chu()
 28 {
 29     he=1;en=0;
 30     mem(vis,0);
 31 }
 32 
 33 void get_most_quick()
 34 {
 35     mem(quick,0x7f);
 36     chu();
 37     for(int i=1;i<=n;++i)
 38       for(int j=1;j<=m;++j)
 39         if(a[i][j])
 40         {
 41           dui[++en]=(son){i,j};
 42           quick[i][j]=0;
 43           vis[i][j]=1;
 44             }
 45     while(en>=he)
 46     {
 47         //cout<<0;
 48         son now=dui[he];++he;vis[now.x][now.y]=0;
 49         if(now.x>1&&quick[now.x-1][now.y]>quick[now.x][now.y]+1)
 50         {
 51             quick[now.x-1][now.y]=quick[now.x][now.y]+1;
 52             if(!vis[now.x-1][now.y])
 53             {dui[++en]=(son){now.x-1,now.y};vis[now.x-1][now.y]=1;}
 54         }
 55         if(now.x<n&&quick[now.x+1][now.y]>quick[now.x][now.y]+1)
 56         {
 57             quick[now.x+1][now.y]=quick[now.x][now.y]+1;
 58             if(!vis[now.x+1][now.y])
 59             {dui[++en]=(son){now.x+1,now.y};vis[now.x+1][now.y]=1;}
 60         }
 61         if(now.y>1&&quick[now.x][now.y-1]>quick[now.x][now.y]+1)
 62         {
 63             quick[now.x][now.y-1]=quick[now.x][now.y]+1;
 64             if(!vis[now.x][now.y-1])
 65             {dui[++en]=(son){now.x,now.y-1};vis[now.x][now.y-1]=1;}
 66         }
 67         if(now.y<m&&quick[now.x][now.y+1]>quick[now.x][now.y]+1)
 68         {
 69             quick[now.x][now.y+1]=quick[now.x][now.y]+1;
 70             if(!vis[now.x][now.y+1])
 71             {dui[++en]=(son){now.x,now.y+1};vis[now.x][now.y+1]=1;}
 72         }
 73     }
 74 }
 75 
 76 void bfs()
 77 {
 78     mem(d,0x7f);
 79     chu();dui[++en]=pos[0];vis[pos[0].x][pos[0].y]=1;
 80     d[pos[0].x][pos[0].y]=0;
 81     while(en>=he)
 82     {
 83         son now=dui[he];++he;vis[now.x][now.y]=0;
 84         //d[now.x][now.y]=minn(d[now.x][now.y],now.bushu);
 85         if(now.x==pos[1].x&&now.y==pos[1].y)continue;
 86         int temp=maxn(d[now.x][now.y],quick[now.x][now.y]);
 87         if(now.x>1&&d[now.x-1][now.y]>temp)
 88         {
 89             d[now.x-1][now.y]=temp;
 90             if(!vis[now.x-1][now.y])
 91             {dui[++en]=(son){now.x-1,now.y};vis[now.x-1][now.y]=1;}
 92         }
 93         if(now.x<n&&d[now.x+1][now.y]>temp)
 94         {
 95             d[now.x+1][now.y]=temp;
 96             if(!vis[now.x+1][now.y])
 97             {dui[++en]=(son){now.x+1,now.y};vis[now.x+1][now.y]=1;}
 98         }
 99         if(now.y>1&&d[now.x][now.y-1]>temp)
100         {
101             d[now.x][now.y-1]=temp;
102             if(!vis[now.x][now.y-1])
103             {dui[++en]=(son){now.x,now.y-1};vis[now.x][now.y-1]=1;}
104         }
105         if(now.y<m&&d[now.x][now.y+1]>temp)
106         {
107             d[now.x][now.y+1]=temp;
108             if(!vis[now.x][now.y+1])
109             {dui[++en]=(son){now.x,now.y+1};vis[now.x][now.y+1]=1;}
110         }
111     }
112 }
113 
114 void out11()
115 {
116     printf("\n");
117     for(int i=1;i<=n;++i)
118     {
119         for(int j=1;j<=m;++j)
120           printf("%d ",quick[i][j]);
121         printf("\n");
122     }
123     printf("\n");
124 }
125 
126 int main(){
127     //freopen("swan11.in","r",stdin);
128     scanf("%d%d",&n,&m);
129     for(int i=1;i<=n;++i)
130       for(int j=1;j<=m;++j)
131       {
132             a[i][j]=read();
133             if(a[i][j]==2)pos[++hhh]=(son){i,j};
134         }
135     
136     get_most_quick();
137     //out11();
138     bfs();
139     cout<<d[pos[1].x][pos[1].y];
140     //while(1);
141     return 0;
142 }