BZOJ 1600

开始刷一些USACO月赛题了..

这题简单递推就不说了.

然后我们发现暴力递推是$O(n^2)$的.看起来非常慢.

这道题拥有浓厚的数学色彩,因此我们可以从数学它的规律上找突破口.

(于是暴力大法好,打表出奇迹.)

n: 1 2 3 4 5 6 7  8  9...
r: 0 0 0 1 4 6 16 19 40

好像完全没有规律,怎么办?

就这么交上去吧,反正不会超时.

然后我们A了这道题,仍然感到不爽.怎么办?

Plot!(擦,我要搞个自己的数学软件!!)

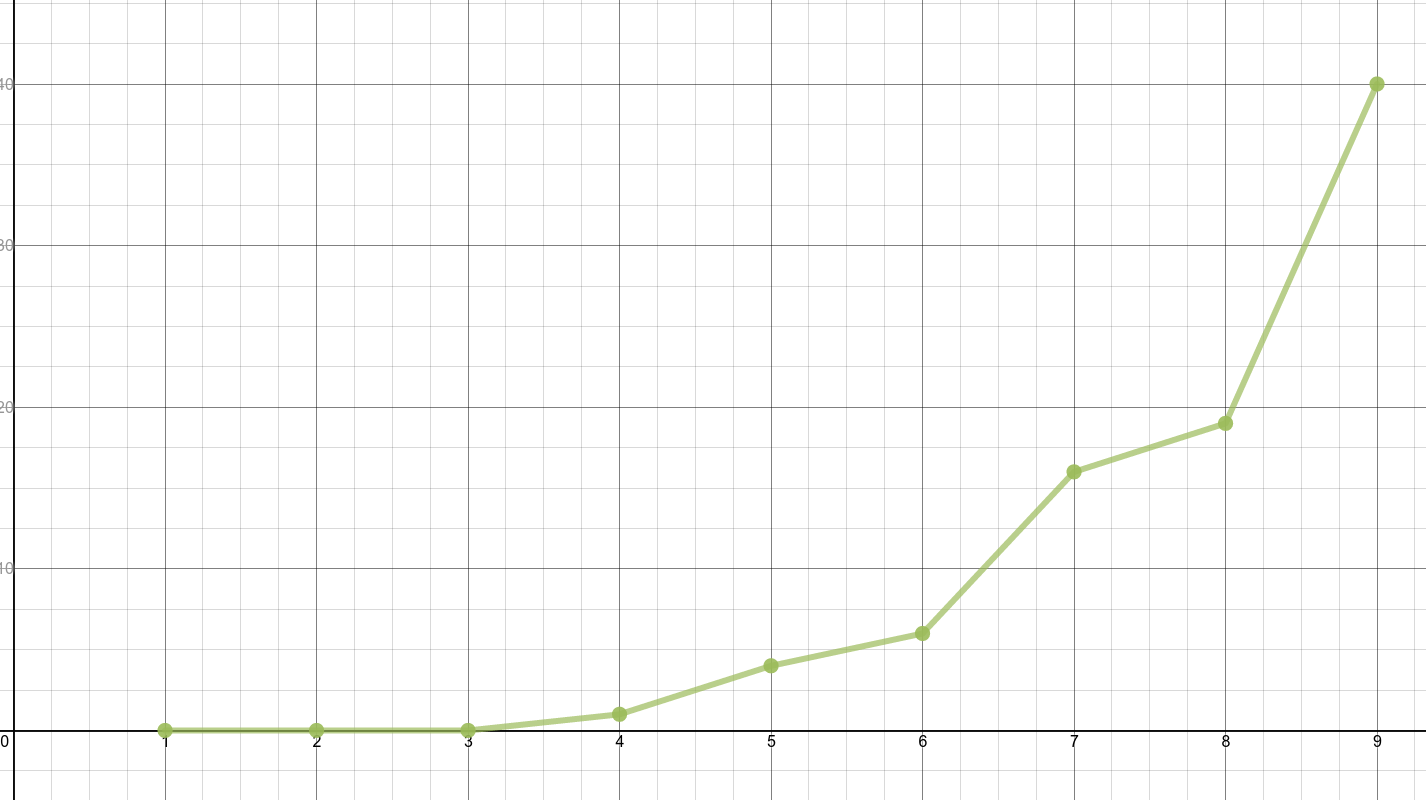
我十分感动...

一看就不是多项式嘛= =!...

////////////////////////////////////////////////////////////

然后我发现我错了.

注意到奇数与偶数之间的间隔,每次都是增加1的.

那么我就把偶数的拿去问了OEIS,它说是一个多项式.

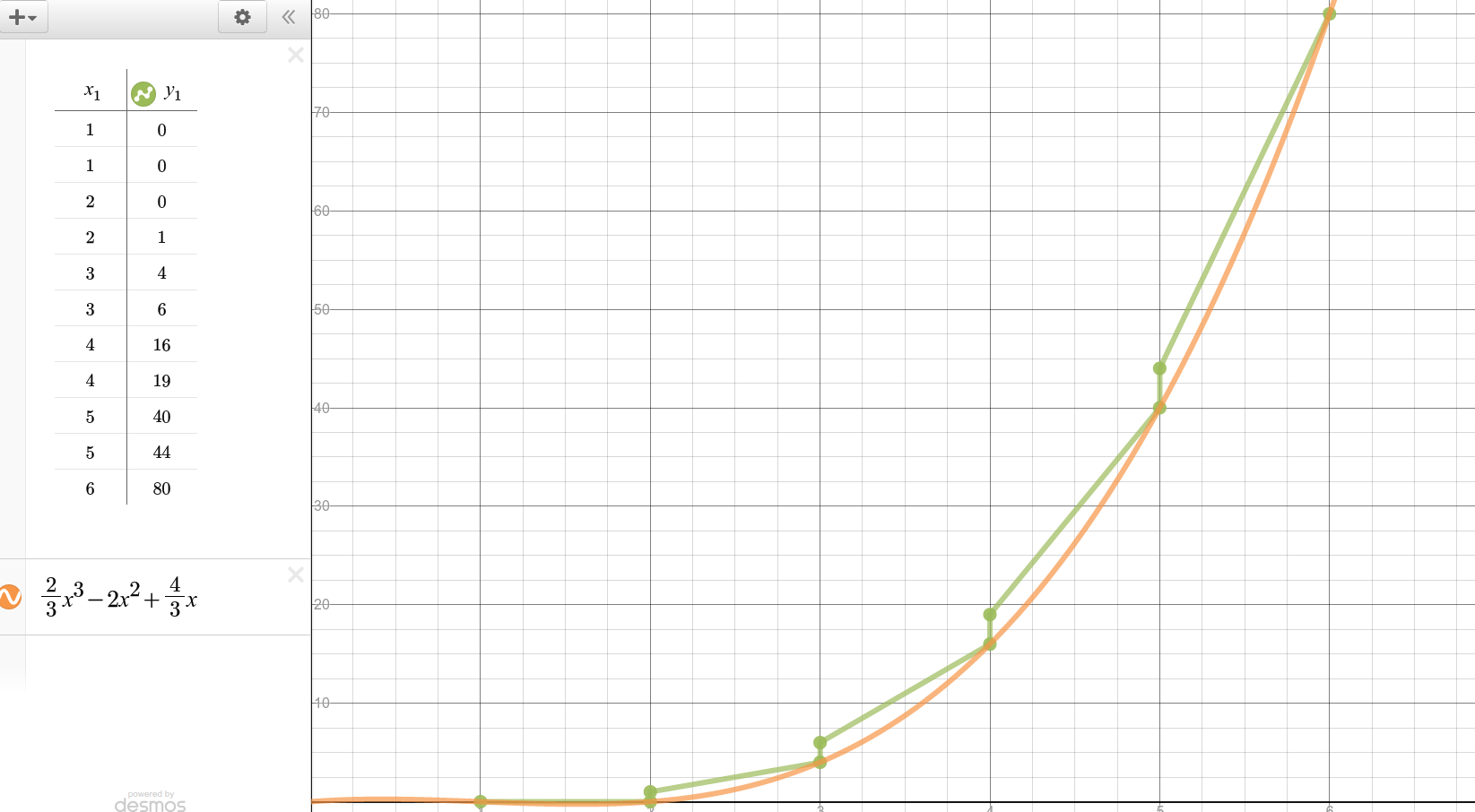
我感受到了这个世界深深的奇妙性...

对就是那个$\frac{2}{3}x^3-2x^2+\frac{4}{3}x$.

接下来就发生了顺理成章的事情.

#include<cstdio>
long long n,m,mx;
int main(){
    scanf("%lld",&n);
    ++n;
    m=n/2;
    mx=((2*m-6)*m+4)*m;
    if(m*2==n){
        printf("%lld\n",mx/3);
    }else{
        printf("%lld\n",mx/3+m-1);
    }
	return 0;
}

转载于:https://www.cnblogs.com/tmzbot/p/4507683.html