二叉搜索树

二叉搜索树

二叉搜索树

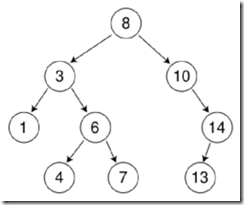
又称二叉排序树，它或者是一棵空树，或者是具有下列性质的二叉树：若它的左子树不为空，则左子树上所有节点的值均小于它的父节点的值，若它的右字树不为空，则右子树上所有节点的值均大于它的父节点的值，它的左右子树叶分别是二叉排序树。二叉排序树能高效的实现查找，插入，删除。比较复杂的是删除操作后如何安排子节点.

插入节点

• 若当前二叉树为空，则插入的元素为根节点
• 若插入的元素小于根节点则在左子树中插入，若大于跟节点则在右子树中插入，递归执行此过程知道找到正确位置将元素插入

删除节点分几种情况:

• 叶子节点：只要把指向该节点的指针指向空
• 只有一个子节点的节点：只要把指向该节点指针指向其子节点就可以
• 有两个子节点的节点:在左子树中查找前驱节点，如节点A，将A的值与与被删除节点进行交换，删除A节点

两个概念:

前驱节点: 左子树中最大的节点

后继节点:右子树种的最小节点

---

源代码namespace BST
{
    public class Node
    {
        public int Value;
        public Node Left;
        public Node Right;
    }
    public class BSTree
    {
        private Node root;
        public void Insert(int x)
        {
            Node v = new Node() { Value = x };
            if (root == null)
            {
                root = v;
                return;
            }
            Node preNode = PosToInsert(x);
            if (preNode.Value > x)
            {
                preNode.Left = v;
            }
            else
            {
                preNode.Right = v;
            }
        }
        //return decessor node, the biggest node in left subtree of x
        private Node Predecessor(Node x)
        {
            if (x == null || x.Left == null)
            {
                return null;
            }
            Node node = x.Left;      
            while (node.Right != null)
            {            
                node = node.Right;
            }
            return node;
        }
        private Node ParentNode(Node node)
        {
            return ParentNode(node.Value);
        }
        private Node ParentNode(int x)
        {
            Node node = root;
            Node parent = node;
            while (node != null)
            {
                if (node.Value == x)
                {
                    return parent;
                }
                parent = node;
                if (node.Value > x)
                {
                    node = node.Left;
                }
                else
                {
                    node = node.Right;
                }
            }
            throw new Exception(string.Format("{0} has no parent",x));
        }
        //return a node ,should insert x as a child to it
        private Node PosToInsert(int x)
        {
            Node node = root;
            Node posToInsert = null;
            while (node != null)
            {
                posToInsert = node;
                if (node.Value == x)
                {
                    throw new Exception(string.Format("{0} already exist in tree", x));
                }
                else if (node.Value > x)
                {
                    node = node.Left;
                }
                else
                {
                    node = node.Right;
                }
            }
            return posToInsert;
        }
        public Node Search(int x)
        {
            return Search(root, x);
        }
        public Node Search(Node node, int x)
        {
            if (node == null)
            {
                return null;
            }
           
            if (node.Value == x)
            {
                return node;
            }
            else if (node.Value > x)
            {
                return Search(node.Left, x);
            }
            else
            {
                return Search(node.Right, x);
            }
        }
        public void Remove(int x)
        {
            Node node=Search(x);
         
            if (node == null)
            {
                throw new Exception(string.Format("{0} not exist in tree",x));
            }
         
            if (node.Left == null && node.Right == null)
            {
                node = null;
            }                  
            else if (node.Left != null && node.Right != null)
            {
                Node preNode = Predecessor(node);
                Node parentNode = ParentNode(preNode);
                Swap(ref preNode.Value,ref node.Value);
                if (Object.ReferenceEquals(preNode, parentNode.Left))
                {
                    parentNode.Left = null;
                }
                else
                {
                    parentNode.Right = null;
                }
            }
            else if (node.Left != null)
            {
                Node parentNode = ParentNode(node);
                if (Object.ReferenceEquals(node, parentNode.Left))
                {
                    parentNode.Left = node.Left;
                }
                else
                {
                    parentNode.Right = node.Left;
                }                
            }
            else if (node.Right != null)
            {
                Node parentNode = ParentNode(node);
                if (Object.ReferenceEquals(node, parentNode.Left))
                {
                    parentNode.Left = node.Right;
                }
                else
                {
                    parentNode.Right = node.Right;
                }
            }
        }
        public override string ToString()
        {
            return Tree(root);
        }
        private string Tree(Node node)
        {
            if (node == null)
            {
                return string.Empty;
            }
            string left = Tree(node.Left);
            string right = Tree(node.Right);
            if (!string.IsNullOrEmpty(left) || !string.IsNullOrEmpty(right))
            {
                return string.Format("{0}({1},{2})", node.Value, Tree(node.Left), Tree(node.Right));
            }
            else
            {
                return node.Value.ToString();
            }
        }
        public static void Swap(ref int x, ref int y)
        {
            int temp = x;
            x = y;
            y = temp;
        }
    }
}

posted on 2016-04-16 19:54 哨兵 阅读( ...) 评论( ...) 编辑 收藏

转载于:https://www.cnblogs.com/phenixyu/p/5399201.html