tarjan与有向图联通性__强连通分量,追溯值

　　对于一个有向图,若任意两个节点x,y都有x到y的路径和y到x的路径,称它为强联通图.一个有向图的极大强联通子图被称为强联通分量.这里的极大与无向图里的极大双联通 子图类似,对于一个极大强联通子图A,不存在子图B也是强联通子图且A⊆B.

　　求有向图的强连通分量又要运用到tarjan算法.先对于有向图中的边进行定义:dfs确定dfs序后,对于一个x指向y的边,如果x是y的父节点称为树枝边,x是y的祖先(x位于y到根节点的路径上)称为前向边,y是x的祖先(y位于x到根节点的路径上)称为后向边.这四种都不是的话称为横叉边.可以发现树枝边们一定可以组成前向边的等效的路径,所以前向边没有用,完全可以删去.后向边一定能和树枝边组成一个环,从而构成一圈强连通的节点,美滋滋.最后一种横向边能构成环当且仅当y有到达x的路径.如何找到后向边与横向边构成的环呢?栈又出场了.

　　我们在dfs(代码中指tarjan)的时候维护一个栈,要求当访问x的时候栈内存放 x的祖先和访问过的节点里存在路径到达x的祖先的节点们,为什么要存"存在路径到达x的祖先的节点"呢?因为如果存在横叉边(x,它),他们就可以构成环,而环意味着强连通分量.然后来引入一个"追溯值low[]"的概念:x的low[x]定义为min(访问x时栈内节点时间戳最小值,从x的子树出发能到达的节点时间戳最小值);

把x入栈,low[x]=dfn[x]=++tot;
枚举所有出边,第一个y没访问过的边为树枝边,tarjan进入,low[x]=min(low[x],low[y]).对于其他的访问过的在栈中的y可以更新low[x]=min(low[x],dfn[y]);
判断if(low[x]==dfn[x])弹出栈中元素直到x出栈.

计算low的方法论

　　然后就可以开心的记录有向图强连通分量了:若low[x]==dfn[x],用vector+stack把栈里剩下来的点放在一个强连通分量里.

　　

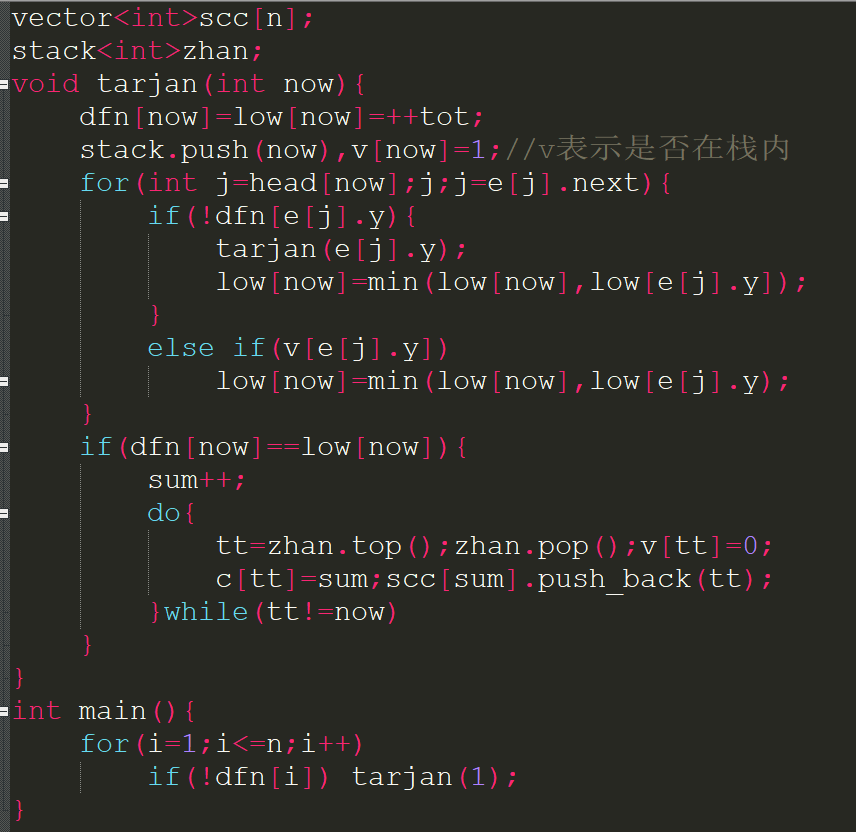
　　上面的tarjan()里已经记录了每个点所在的强连通分量的代表:c[i].那么缩点的时候完全可以枚举每条边,若c[x]!=c[y]就把x和y连边,最后形成一个大小为sum的新图.

　　有向图的联通性就先这样了.

转载于:https://www.cnblogs.com/qywyt/p/10242446.html