图

 

基本术语

• 简单路径：顶点不重复出现的路径
• 无向完全图：任意两个结点间都存在边
• 有向完全图：任意两个结点间都存在方向相反的两条弧
• 回路：第一个顶点与最后一个顶点相同的路径
• 简单图：不存在顶点到其自身的边，且同一边不重复出现

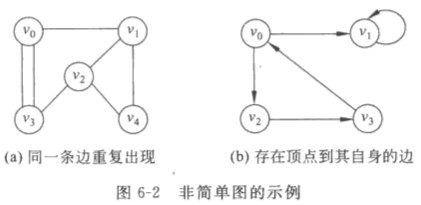
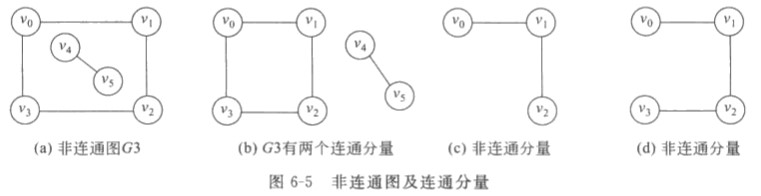
• 连通图：任意顶点之间都有路径
• 连通分量：连通图的极大连通子图

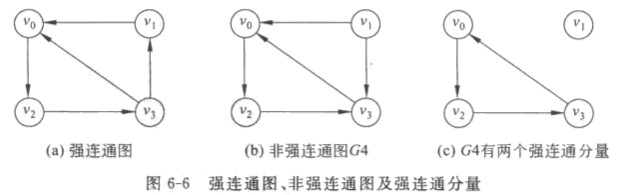
• 强连通图：从任意顶点 i 到顶点 j 均有路径的有向图
• 强连通分量：强连通图的极大连通子图

• 生成树：

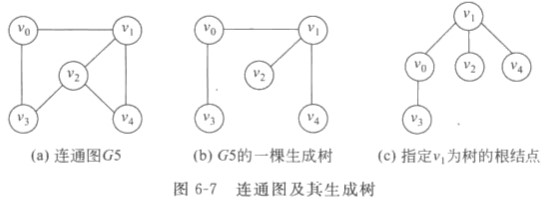
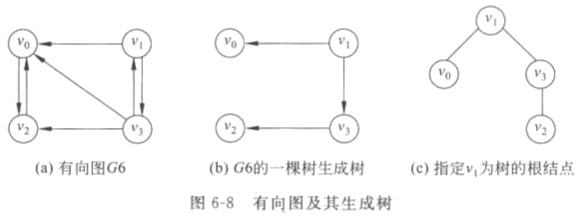
• 生成森林

---

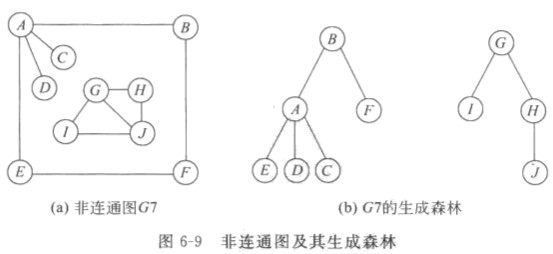
存储结构

邻接矩阵

 

 

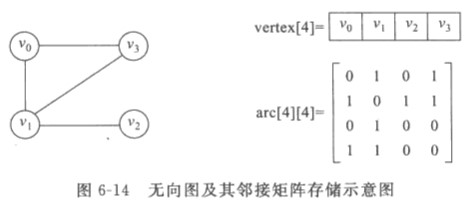
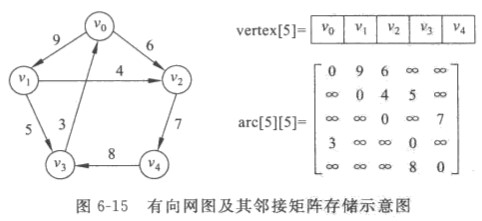
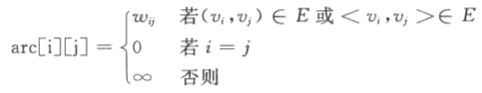
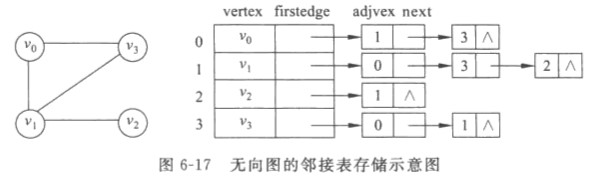
邻接链表

 

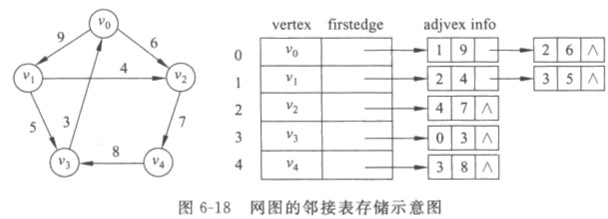
十字链表

邻接多重表

---

图的遍历

1、给顶点编号
2、遍历所有顶点：多次重复从某一顶点出发遍历 + 访问标志记录顶点是否已经访问

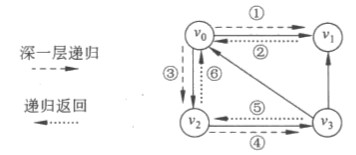
深度优先

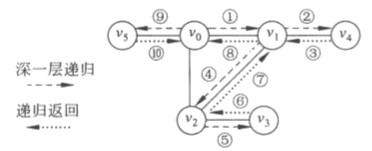
邻接矩阵实现

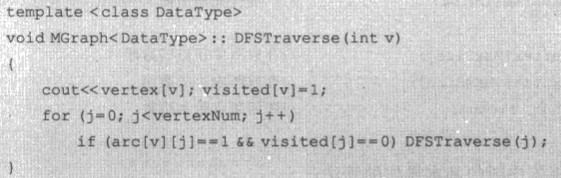
邻接表实现

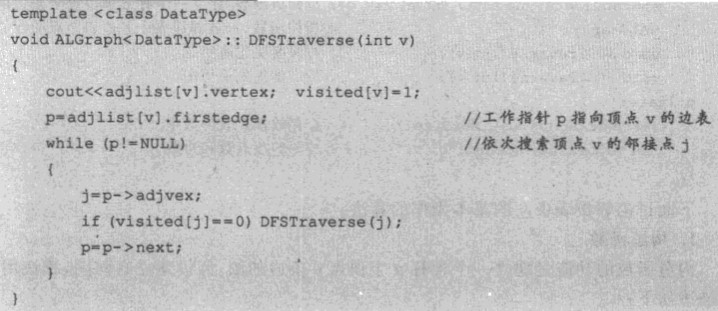
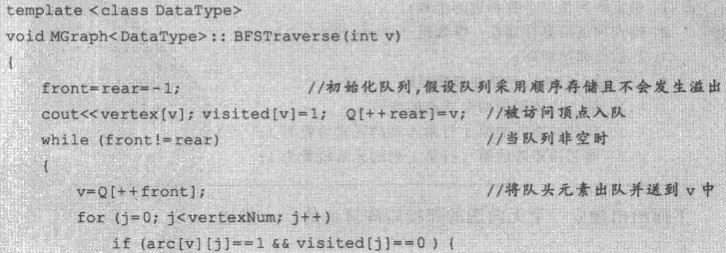
广度优先

邻接矩阵实现

邻接表实现

 

---

最小生成树

MST性质

Prim算法

（逐个加入）

存储结构： 不断读取任意两个顶点边的权值：邻接矩阵

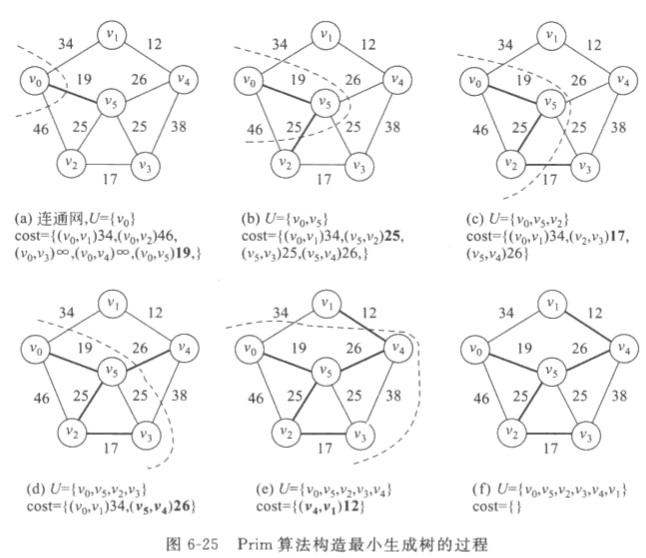
关键：找到连接U与U-V的最短边来扩充生成树T

 

 

Kruskal算法

（寻不回路边）

存储结构： 依次对图的边操作：邻接表

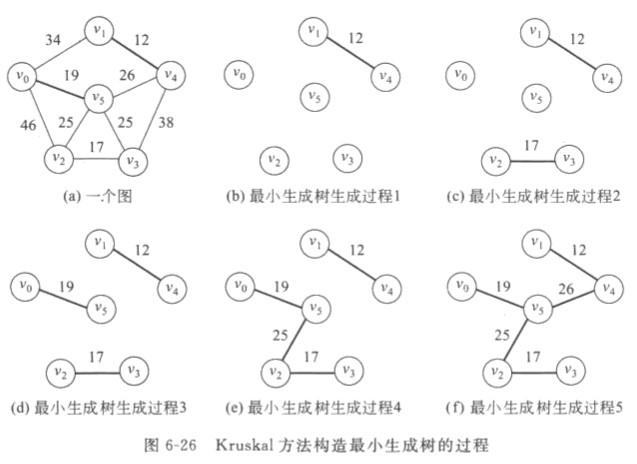
关键：如何判断两个顶点是否位于两个连通分量（即是否与生成树的边形成回路）

 

---

最短路径

Dijkstra算法

（逐个加入+不断修改最优路径）（贪心算法）

存储结构：快速读取任意两结点的边的权值：邻接矩阵

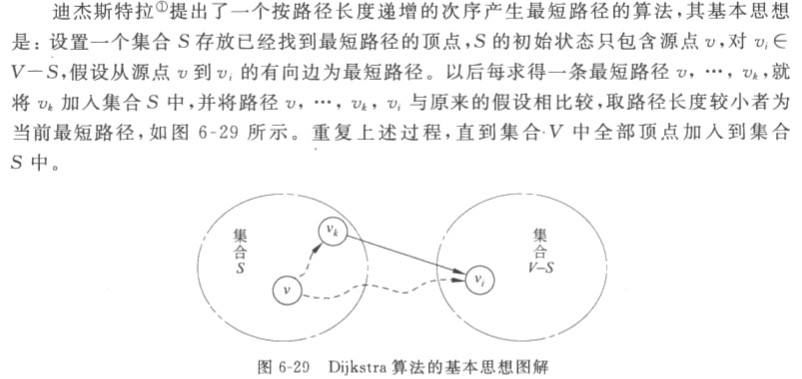
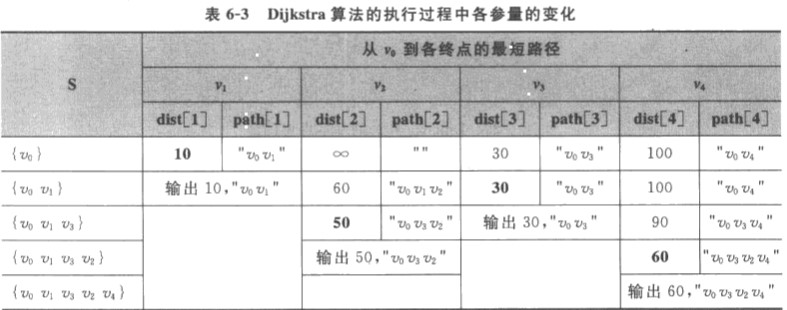
辅助数组：

dist[i] 表示当前找到的从源结点到终点结点的最短路径长度

path[i] 表示 当前找到的从源结点到终点结点的具体最短路径结点（可用字符串表示）

s[n] ：源点到已生成终点的集合

 

 

参考：《数据结构（C++版）》王红梅

 

 

 

 

来自为知笔记(Wiz)

转载于:https://www.cnblogs.com/Doing-what-I-love/p/5445435.html