过椭圆外一点引两条切线方程_圆锥曲线之椭圆篇

圆锥曲线历年来都是高考场上的重头戏，大约占了二十多分，其中包括选择题、填空题以及大题。本文特别整理了高中学习中椭圆的相关结论，希望能对大家有所帮助！

注：本文仅以

为例，

为左右焦点，

为左右顶点。

目录：
（一）定义
（二）性质
（三）椭圆的切线、法线定理
（四）点与椭圆的关系
（五）直线与椭圆的关系
（六）神奇的

（七）其他椭圆的相关结论

---

（一）定义

1.第一定义：平面内与两定点

、

的距离的和等于常数

，即

的动点

的轨迹叫做椭圆。

长轴=

,短轴=

，焦距=

2.第二定义：椭圆平面内到定点

（即焦点）的距离和到定直线

（

不在

上）的距离之比为常数

（即离心率

，

）的点P的轨迹是椭圆。

准线（即定直线）=

（焦点在x轴或y轴上均相同）

（二）性质

1.取值范围：焦点在x轴上时，

2.对称性：对称轴（长轴，短轴）为x轴和y轴，对称中心为原点

3.焦半径：焦点在x轴上时，

（

分别为左右焦点）；焦点在y轴上时，

（

分别为上下焦点）。

4.通径：过焦点的垂直于x轴（或y轴）的直线与椭圆的两交点A，B之间的距离，即

，半通径

。

5.离心率：

离心率越小越接近于圆，越大则椭圆就越扁。

（三）椭圆的切线、法线定理

1.椭圆的切线定理：设

为椭圆C的两个焦点，P为C上任意一点。若直线

切椭圆C于点P，且A和B在直线上位于P的两侧，则

。（也就是说，椭圆在点P处的切线即为

的外角平分线所在的直线）

2.椭圆的法线定理：设

为椭圆C的两个焦点，P为C上任意一点。若直线

为C在P点的法线，则

平分

。

（四）点与椭圆的关系

点M

椭圆

点在椭圆内：

点在椭圆上：

点在椭圆外：

（五）直线与椭圆的关系

直线

与椭圆联立方程组得：

1. 相切
   ，相离
   无交点，相交
   。
2. 椭圆与直线交于
   两点，弦长公式
   或

（六）神奇的

1.若A、B是椭圆上关于原点对称的两点，M是椭圆上异于A、B的点，则

。

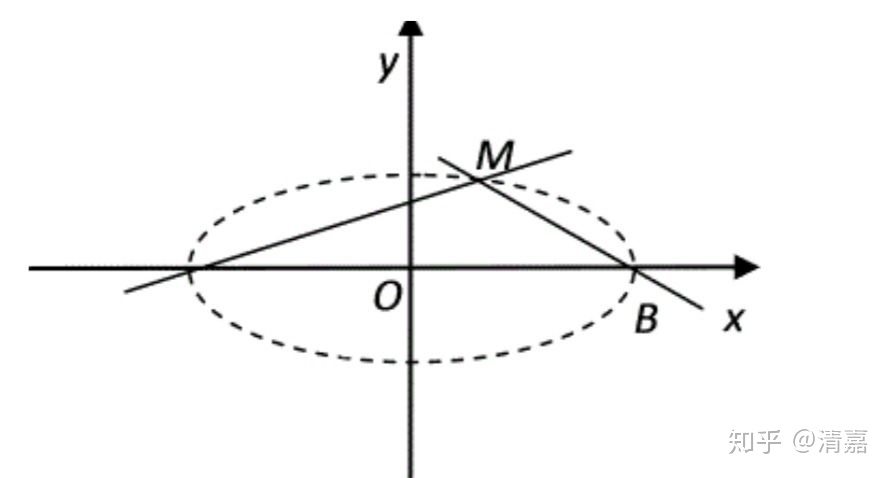
2.若AB是椭圆上不垂直于对称轴的弦，M为AB的中点，则

。

3.若

是椭圆上不垂直与对称轴的切线，M为切点，则

。

该结论为上一结论的极限化

4.椭圆上的点与椭圆长轴（事实上只要是直径都可以）两端点连线的斜率之积是定值，定值为

；若长轴平行于y轴，比如焦点在y轴上的椭圆，可以得到斜率之积为

。

（七）其他椭圆的相关结论

1.参数方程：

。

求解椭圆上点到定点或到定直线距离的最值时，用参数坐标可将问题转化为三角函数问题求解

2.面积：

（当

时即为圆的面积）

3.焦点三角形：对于点M处 ，

4.标准形式的椭圆在

点的切线就是 ：

，椭圆切线的斜率是

。

5.

6.如果中心在原点，但焦点的位置不明确在X轴或Y轴时，方程可设为

。

7.椭球体方程：

，体积：

（当

时，即为球的体积）

8.

为椭圆的焦点弦，则过A、B的两条切线的交点M必在相应准线上。

9.以焦点弦为半直径圆一定与对应的准线相离。

10.以焦半径为直径的圆与以长轴为直径的圆相切。

11.三角形

在边

或

上的旁边圆一定与

切于

或

。

12.椭圆中，记焦点三角形的底角分别为

和

，则该椭圆的离心率为

。

---