HGOI 20190816 省常中互测8

Problem A 

有两条以(0,0)为端点，分别经过(a,b)，(c,d)的射线，你要求出夹在两条射线
中间，且距离(0,0)最近的点（x,y）

对于$100\%$的数据满足$1 \leq T \leq 10^6 , 0 \leq a,b,c,d \leq 10^9$

Solution : 

　　每次删除一个下面那条线斜率下取整这块三角形，然后将y坐标下移，

　　每一次分治下去，最后一定会存在一个时刻$(1,1)$合法，此时回溯回去即可。

　　由于分治前后，线段的相对位置不变，不会存在新的点更优，所以最后生成的答案一定是最优的。

　　每次查询的复杂度大约是$O(n)$的。

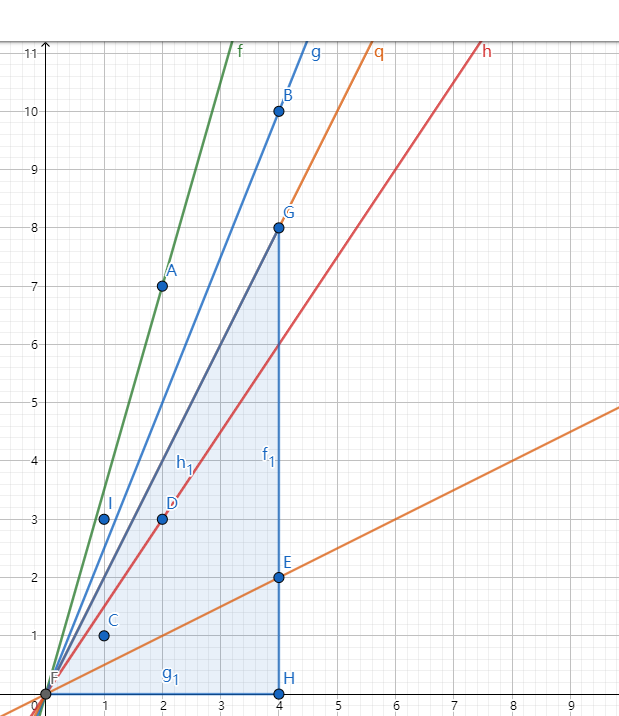
　　具体可以看下面$a = 2,b = 7,c = 4,d = 10$的求值方法。

　　

 

# include <bits/stdc++.h>
# define int long long
using namespace std;
void work(int a,int b,int c,int d,int &x,int &y)
{
    if (a<b&&c>d) { x=1,y=1; return; }
    if (a*d>b*c) work(c,d,a,b,x,y);
    else if (a>=b) work(b,a,d,c,y,x);
    else {
        int t=d/c;
        work(a,b-t*a,c,d-t*c,x,y);
        y+=t*x;
    }
}
main()
{
    int T; scanf("%lld",&T);
    while (T--) {
        int a,b,c,d; scanf("%lld%lld%lld%lld",&a,&b,&c,&d);
        int x,y;  if (a*d>b*c) swap(a,c),swap(b,d);
        work(a,b,c,d,x,y); printf("%lld %lld\n",x,y);
    }
    return 0;
 }

A.cpp

Problem B graph

给出$n$个点$m$条边的连通二分图$G$ ,给出$Q$组询问，每次求出$u,v$路径上(不一定是简单路径)的权值最大值。

一条路径的权值定义为，这条边经过所有节点的异或和，同一个点经过多次将会被计算多次。

对于$100\%$的数据满足$1 \leq n,m,Q\leq t\times 10^5$

Solution : 二分图性质题。

　　对于一个图$G$是二分图，满足一定是两个集合的点来考虑。

　　我们考虑$u - v$的一条路径，如果走简单路径就是$u \ xor \ v$的权值，如果走一个来回，那么就是$0$的权值。

　　所以，对于任意两点的任意一条路径，我们都可以考虑两个相邻点权值是否被异或到路径的答案中，可以同时取反。

　　对于询问中处在相同集合的两个点，路径经过点的数目一定是奇数，选择若干个点对翻转一定会造成奇数个节点的权值被选择（一个极端的例子就是什么节点都不翻转状态）

　　由于二分图的连通性，问题就等价于求在所给点集里找出奇数个点，使他们的异或和最大。

　　在询问中处在相异集合里的两个点，路径经过点的数目一定是偶数，选择若干个点对翻转一定会造成偶数个节点的权值被选择（一个极端的例子就是什么节点都不翻转状态）

　　由于二分图的连通性，问题就等价于求在所给点集里找出偶数个点，使他们的异或和最大。

　　在所给点集里找出偶数个点，使他们的异或和最大。这个问题可以将相邻两个点的点权插入到线性基里面，然后求出线性基中的最大值即可。

　　在所给点集里找出奇数个点，使他们的异或和最大。这个问题可以将相邻两个点的点权插入到线性基里面，强制地任意的取一个节点必须被异或，然后求出线性基中的最大值即可。

　　由于可以预处理这两个答案，最后询问的复杂度就是$O(1)$的，最终，本题的复杂度就是$O(n+Q)$的。

# include <bits/stdc++.h>
using namespace std;
const int N=5e5+10;
struct rec{
    int pre,to;
}a[N<<1];
int head[N],n,m,q,val[N],tot,col[N]; 
void adde(int u,int v)
{
    a[++tot].pre=head[u];
    a[tot].to=v;
    head[u]=tot;
}
struct Linear_Basis{
    int d[31];
    Linear_Basis() {
        memset(d,0,sizeof(d));
    }
    void insert(int x) {
        for (int i=30;i>=0;i--)
         if (x&(1<<i)) {
            if (!d[i]) { d[i]=x; break;}
            else x^=d[i];
         }
    }
    int query(int ret) {
        for (int i=30;i>=0;i--)
         if ((ret^d[i])>ret) ret^=d[i];
        return ret; 
    }
}B;
void dfs(int u,int c)
{
    col[u]=c;
    for (int i=head[u];i;i=a[i].pre) {
        int v=a[i].to; if (col[v]) continue;
        dfs(v,3-c);
    }
}
int main()
{
    scanf("%d%d%d",&n,&m,&q);
    for (int i=1;i<=n;i++) scanf("%d",&val[i]);
    for (int i=1;i<=m;i++) {
        int u,v; scanf("%d%d",&u,&v);
        adde(u,v); adde(v,u);
    }
    dfs(1,1);
    for (int i=1;i<n;i++) B.insert(val[i]^val[i+1]);
    int same = B.query(val[1]);
    int diff = B.query(0);
    while (q--) {
        int u,v; 
        scanf("%d%d",&u,&v);
        if (col[u]==col[v]) printf("%d\n",same);
        else printf("%d\n",diff);
    }
    return 0;
 }

B.cpp

Problem C geo

平面直角坐标系中有$n$个点$(x_i,y_i)$,求出有多少个二次函数$y = x^2 + bx +c$经过至少两个点,并且任何点都不在这个函数的上方。

对于$100\%$的数据，满足$n\leq 2\times 10^5$

Solution :

　　对于点$(x,y)$在$y = x^2 + bx + c$下方的条件是$x^2 + bx + c \geq y$

　　化简后就是$bx + c\geq y - x^2 $

　　对于所有的点$(x,y)$都是一定的，如果我们把每个点的坐标转化为$(x,y-x^2)$，

　　问题就转化为求一个一次函数$y = bx + c$使得这个一次函数至少经过两个点并且在所有点上方。

　　问题就等价于求出一个点集凸包的上部的边的条数。

　　即所有在左极点和右极点连线严格上方的点数+1。

　　复杂度就是$O(n)$的。

#include<bits/stdc++.h>
#define ll long long
#define inf (1e18)
using namespace std;
struct p{double x,y;}a[200010],s[200010],l,r;
ll n,k=1,top=1,ans;
double cross(p a,p b,p c){return(b.x-a.x)*(c.y-a.y)-(b.y-a.y)*(c.x-a.x);}
double dis(p a,p b){return sqrt((b.y-a.y)*(b.y-a.y)+(b.x-a.x)*(b.x-a.x));}
bool cmp(p x,p y)
{
    double tmp=cross(a[1],x,y);
    return tmp>0||(tmp==0&&dis(a[0],x)<dis(a[0],y));
}
int main()
{
    scanf("%lld",&n);
    for(ll i=1;i<=n;i++)scanf("%lf%lf",&a[i].x,&a[i].y),a[i].y-=a[i].x*a[i].x;
    for(ll i=1;i<=n;i++)if((a[k].y>a[i].y)||(a[k].y==a[i].y&&a[i].x<a[k].x))k=i;
    swap(a[k],a[1]),sort(a+2,a+1+n,cmp),s[1]=a[1];
    for(ll i=2;i<=n;i++)
    {
        while(top>1&&cross(s[top-1],a[i],s[top])>=0)top--;
        s[++top]=a[i];
    }
    l={inf*1.0,inf*1.0},r={inf*-1.0,inf*-1.0};
    for(ll i=1;i<=top;i++)
    {
        if(s[i].x<l.x)l=s[i];else if(s[i].x==l.x&&s[i].y>l.y)l=s[i];
        if(s[i].x>r.x)r=s[i];else if(s[i].x==r.x&&s[i].y>r.y)r=s[i];
    }
    for(ll i=1;i<=top;i++)if(cross(l,r,s[i])>0)ans++;
    printf("%lld\n",ans+1);
    return 0;
}

C.cpp

 

转载于:https://www.cnblogs.com/ljc20020730/p/11364618.html