的范数最大_矩阵的范数 之 二范数

矩阵的范数 之 常用不等式(一)

上一篇文章根据矩阵范数的定义介绍了 范数的相容性矩阵的范数 之 常用不等式 。今天接着利用范数的定义，解释一下矩阵的二范数为什么等于它的奇异特征值的最大值。欢迎大家批评，指正，留言，分享！

---------------------------------------------------------------------------------------------------------------------------------

---------------------------------------------------------------------------------------------------------------------------------

 矩阵常用范数为诱导范数(induced norm)，定义为

 

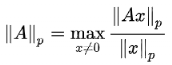
P代表是什么范数(1-，2-等范数啦)。  因为本文介绍二范数，我们只需令p=2, 即

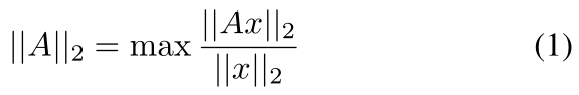
为求(1)式右边的max 这一项， 只需做如下简单分析(我们只分析实数矩阵，复数矩阵一样的道理。目前为止，我还未遇到过复数矩阵的分析，按下不表。)

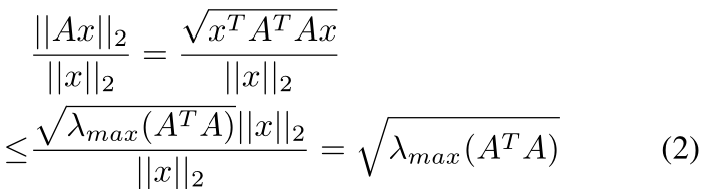
其中不等式(2)用到了一个常用公式，对于一个对称矩阵，

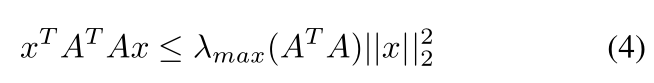
好像公式有点多了，马上给结论。 由不等式(2)可得，

    

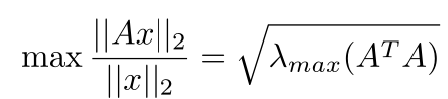
   结合公式(1)就得出了

      

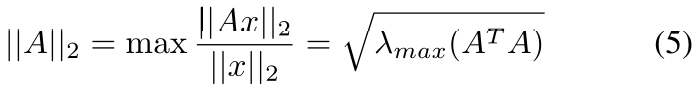
问题得证， 矩阵二范数等于它的奇异特征值的最大值。

稍微一点延伸， 我们用作分析的矩阵经常是对称矩阵， 那么对称矩阵的二范数等于什么呢？

如果A是对称矩阵，通过(5)就可以得到，它的二范数就等于A的绝对值最大的那个特征值(啰嗦一句，因为)。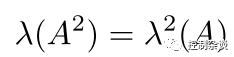

以上！