图像傅里叶变换实战：从频谱分析到应用

小鹿嘻嘻

于 2025-06-20 13:50:34 发布

阅读量1.1k

点赞数 27

CC 4.0 BY-SA版权

本文链接：https://blog.youkuaiyun.com/weixin_28793831/article/details/148810672

本文还有配套的精品资源，点击获取

简介：傅里叶变换是数字信号处理的关键，尤其在图像处理中有着重要的应用，如获取频谱图及图像的频率分析。本文解析了“fft.zip”压缩包中的文档，重点介绍了二维离散傅里叶变换（2D DFT）及其在图像频域转换、频率分析、滤波去噪和图像压缩等方面的应用。
fft.zip_傅里叶图像_傅里叶变换_傅里叶频谱图_图像傅里叶

1. 傅里叶变换概述

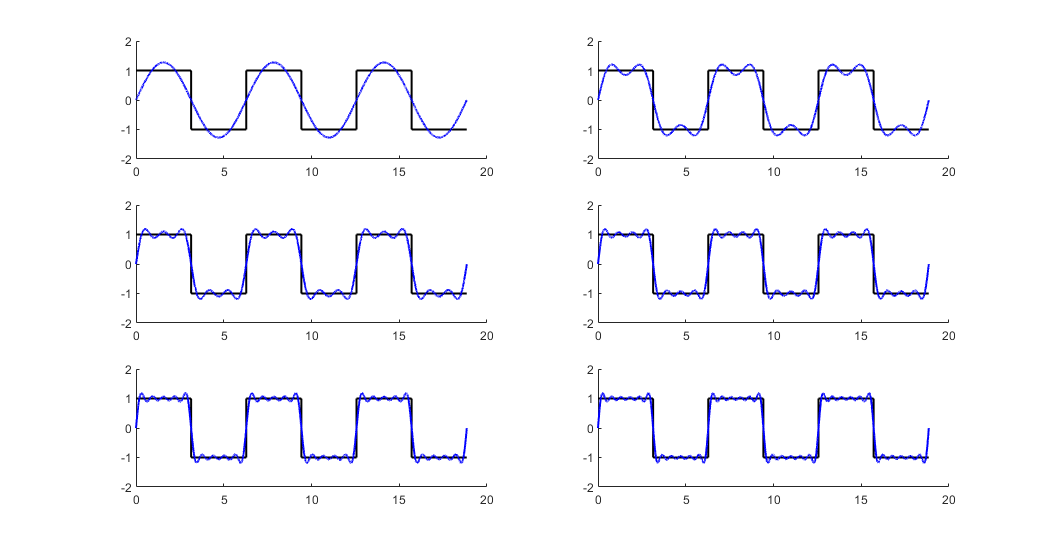
傅里叶变换是数学领域中一种将复杂信号分解为简单正弦波和余弦波的方法，从而使我们能够理解信号的频率成分。它对于电子工程、信号处理、图像分析乃至数据压缩等领域至关重要。

傅里叶变换的起源和发展

傅里叶变换以法国数学家让-巴蒂斯特·约瑟夫·傅里叶的名字命名，他在19世纪初提出这一理论，最初用于解决热传导问题。后来，这一理论被扩展到各种信号分析领域。

傅里叶变换的主要应用领域

傅里叶变换的核心应用包括频域分析、信号处理、图像压缩等。通过变换到频域，工程师和科学家们可以更容易地识别信号特征，进行有效的信号或图像处理。在下一章中，我们将深入探讨傅里叶变换在图像处理中的具体应用。

2. 图像频域转换和频谱图的生成

2.1 频域转换基础

频域转换是数字图像处理中的一个基本且重要的步骤，它涉及将图像从空间域转换为频域。在频域中，图像以频率的形式展现，让我们能够分析图像的频率成分。这一过程对于图像处理任务，如边缘检测、特征提取等至关重要。

2.1.1 从空间域到频域的转换

空间域直接反映了图像的像素点布局和颜色信息，而在频域中，图像的结构信息通过频率表示。频率高表示图像变化快，即边缘或纹理部分；频率低则代表平滑区域。从空间域到频域的转换通常使用傅里叶变换来完成。

这里以一段Python代码为例，演示如何将图像进行频域转换：

import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft2, fftshift

def convert_to_frequency_domain(image):
    # 将图像数据转换为二维傅里叶变换
    complex_freq = fft2(image)
    # 为了更好地可视化频谱，应用频移
    shifted_freq = fftshift(complex_freq)
    # 计算幅度谱
    amplitude_spectrum = np.log(np.abs(shifted_freq) + 1) # 幅度谱
    return amplitude_spectrum

# 读取图像并转换为灰度
image = plt.imread('image.jpg')
gray_image = plt.cvtColor(image, plt.COLOR_BGR2GRAY)

# 执行转换
frequency_domain = convert_to_frequency_domain(gray_image)

上面的代码将图像从空间域转换到频域，并对频谱图进行了对数变换，以便于可视化。 fft2 函数执行二维傅里叶变换，而 fftshift 函数则将零频率分量移动到频谱的中心。

2.1.2 频域中的信息表示

频域中的信息以频率的形式展现。频率分布的模式对于理解图像内容非常重要。低频部分通常包含图像的主要结构和大面积色块的信息，而高频部分则携带着细节信息，如边缘和纹理。

频域表示让我们能够轻松地识别和处理这些不同的成分。例如，在图像压缩中，可以去除高频部分，因为在人眼看来，高频信息的丢失对图像的总体感知影响较小。

2.2 频谱图的生成过程

2.2.1 利用傅里叶变换生成频谱图

频谱图是频域表示的一种可视化方式，它显示了不同频率分量在图像中的分布。生成频谱图需要计算图像的二维傅里叶变换，然后对结果进行可视化处理。

import numpy as np
import matplotlib.pyplot as plt

# 假设image是一个二维图像数组
fft_result = np.fft.fft2(image)
fft_shifted = np.fft.fftshift(fft_result)
amplitude_spectrum = np.abs(fft_shifted)

# 使用Matplotlib绘制幅度频谱图
plt.imshow(np.log(amplitude_spectrum + 1), cmap='gray')
plt.title('Frequency Spectrum')
plt.colorbar()
plt.show()

上面的代码段计算了图像的二维傅里叶变换，进行了频移，并对幅度频谱使用对数变换，使得频谱图可视化。

2.2.2 频谱图中信息的解读与分析

频谱图中的亮点表明了图像中频率成分的强弱。通常在频谱图的中心可以看到一个亮点，它代表了图像的直流分量（DC成分），即图像的平均亮度。从中心向外，频谱逐渐表示更高的频率成分。

频谱图的分析对于图像处理非常有用，例如，可以用来检测和增强图像的边缘信息，或者通过滤波去除噪声。

2.3 频谱图的特性与应用

2.3.1 频谱图的物理意义

频谱图的物理意义在于它展现了图像中各种频率分量的强度和分布。频谱图中的强信号表明了图像中对应频率成分的存在，这些信息对于图像分析和处理具有指导作用。

2.3.2 频谱图在图像分析中的应用

频谱图在图像分析中有很多应用，比如在图像增强和恢复中，可以利用频谱信息来突出或减弱某些图像特征。在噪声去除时，可以识别和消除高频噪声成分，而保留对人眼重要的低频成分。

频谱分析不仅可以应用于图像本身，还能帮助我们理解图像处理算法的行为和效果。

2.4 实际应用案例

案例1：图像压缩

在图像压缩任务中，频谱图可以用来确定哪些频率成分对于保持图像质量不是那么重要。例如，在JPEG图像压缩中，高频信息通常会被降低或移除，因为人眼对这些细节的敏感度较低。

# 实际中，通过调整阈值去除高频成分
high_freq_removed = remove高频成分(frequency_domain, threshold)

案例2：边缘检测

频谱图也可用于边缘检测。图像中的边缘表现为高频信号，通过分析频谱图中的高频区域，可以有效地检测出图像中的边缘信息。

# 边缘检测的简单实现
edges = detect_edges(frequency_domain)

在下一章节中，我们将深入探讨如何从频谱图中提取高频与低频信息，并详细讨论这些信息在图像处理中的应用。

3. 高频与低频的图像特征分析

3.1 高频与低频的定义与特征

3.1.1 高频信号与低频信号的区分

在图像处理中，高频和低频的概念通常用来描述信号在频率维度上的特性。低频信号代表图像中的平滑或者缓慢变化的区域，如大面积的均匀区域或渐变色调。相反，高频信号对应图像中的快速变化区域，例如边缘、纹理和细节部分。

3.1.2 高频与低频信号在图像中的表现

高频信号和低频信号在图像中体现为不同的视觉特征。低频区域往往视觉上更加模糊，而高频区域则包含更多的细节信息，对于人眼来说更加锐利和突出。例如，在观看一幅风景画时，天空和海洋等大片单色区域通常是低频信号的体现，而树木的枝叶和山石的轮廓则对应于高频信号。

3.2 高频与低频信息的提取

3.2.1 提取方法与工具

高频与低频信息的提取可以通过多种数字信号处理技术实现，傅里叶变换是其中的关键工具。在频域中，低频信息集中于频谱图的中心区域，而高频信息则分布在周边。常用的方法包括滤波器（例如高通滤波器和低通滤波器）的应用。

一个简单的例子是使用Python语言中的NumPy库进行高低频信息的提取。

import numpy as np
import matplotlib.pyplot as plt
from scipy.fftpack import fft2, ifft2, fftshift

def extract_frequency_components(image):
    # 将图像转为频域
    freq_domain_image = fft2(image)
    # 频域中心化
    freq_domain_image_shifted = fftshift(freq_domain_image)

    # 提取高频成分
    high_pass = np.abs(freq_domain_image_shifted)
    # 提取低频成分
    low_pass = high_pass.copy()
    low_pass[low_pass < np.median(low_pass)] = 0
    return high_pass, low_pass

# 假设有一个灰度图像变量 'img'
high_freq, low_freq = extract_frequency_components(img)

3.2.2 提取后的信号处理

提取出的高低频信号常常需要进一步处理才能被有效使用。比如，在提取高频信号后，可能会使用锐化滤波器来增强边缘和细节，而低频信号则可以通过平滑滤波器来降低噪声和细节，突出大区域的渐变效果。

3.3 高频与低频分析在图像处理中的应用

3.3.1 边缘检测与图像增强

高频信息在图像处理中最重要的应用之一就是边缘检测和图像增强。通过提取和强化图像中的高频信号，可以突出物体的边缘和细节，从而达到增强图像对比度和清晰度的效果。

下面是一个边缘检测的Python代码示例，使用了Canny算法，该算法本质上是高通滤波器的一个应用。

from scipy.ndimage import gaussian_filter
from skimage.feature import canny

def edge_detection(image):
    # 应用高斯滤波器以平滑图像
    filtered_image = gaussian_filter(image, sigma=1)
    # 使用Canny算法检测边缘
    edges = canny(filtered_image)
    return edges

edges = edge_detection(img)

3.3.2 去噪与细节保留策略

在提取高频信号的同时，低频信号对于保持图像的整体亮度和大范围的色彩渐变同样重要。因此，在图像处理中，可以针对低频信号进行滤波去噪，从而保留整体视觉效果的同时，去除图像中的噪声和无关细节。

下面的代码展示了一个简单的滤波去噪过程，其中使用了低通滤波器来去除高频噪声：

def low_pass_filtering(image):
    low_freq_filtered = np.copy(image)
    for i in range(image.shape[0]):
        for j in range(image.shape[1]):
            if i < 3 or i > image.shape[0] - 3 or j < 3 or j > image.shape[1] - 3:
                low_freq_filtered[i, j] = np.mean(image[i-3:i+3, j-3:j+3])
    return low_freq_filtered

low_passed_img = low_pass_filtering(img)

综上所述，通过对高频和低频信息的提取与处理，可以在图像处理中实现边缘增强、去噪、细节保留等多种功能。这些技术是现代图像处理技术中的基础，广泛应用于数字图像编辑、计算机视觉等领域。

4. 二维离散傅里叶变换（2D DFT）的实现

4.1 2D DFT的基本概念

4.1.1 2D DFT的定义与性质

二维离散傅里叶变换（2D DFT）是将二维信号，比如图像，从空间域转换到频域的工具。该变换在图像处理中至关重要，因为它揭示了图像内容在频域中的表示。2D DFT的定义可以表示为：

[
F(u,v) = \sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x,y) \cdot e^{-j2\pi(\frac{ux}{M} + \frac{vy}{N})}
]

其中，(f(x,y)) 是空间域中的图像像素值，(F(u,v)) 是对应的频域表示，(M) 和 (N) 是图像的尺寸，(e) 是自然对数的底数，(j) 是虚数单位。

2D DFT的性质包括线性、平移不变性、旋转对称性、尺度变换等，这些性质使得2D DFT成为分析图像频域特性的强大工具。

4.1.2 2D DFT与一维DFT的区别

一维DFT处理的是一维信号，如音频波形，而2D DFT处理的是二维图像信号。一维和二维DFT的主要区别在于它们各自处理的数据维度不同，这导致了它们在实现和应用上的不同。2D DFT的计算更复杂，因为需要在两个维度上执行变换。

4.2 2D DFT的实现技术

4.2.1 快速傅里叶变换(FFT)算法原理

快速傅里叶变换（FFT）是一种高效计算DFT的算法，由库利-图基算法发展而来。FFT减少了计算DFT所需的乘法次数和加法次数，从而大大提高了计算效率。对于 (N) 点DFT，标准DFT需要 (N^2) 次复数乘法，而FFT仅需要 (N \log_2 N) 次复数乘法。这使得2D DFT在实际应用中变得可行。

4.2.2 编程实现2D DFT

在实际编程中，实现2D DFT通常使用FFT算法。以下是使用Python语言进行2D DFT实现的简单例子，其中使用了 numpy 库来执行FFT操作：

import numpy as np
from numpy.fft import fft2, ifft2

def compute_2d_dft(image):
    # 对图像进行二维离散傅里叶变换
    complex_image = fft2(image)
    magnitude_spectrum = np.abs(complex_image)  # 计算振幅谱
    return magnitude_spectrum

# 示例图像矩阵（灰度值）
image = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# 计算2D DFT
spectrum = compute_2d_dft(image)

# 输出频域表示的振幅谱
print(spectrum)

代码中首先使用 fft2 函数执行二维快速傅里叶变换，然后使用 np.abs 计算复数矩阵的模值，得到频域的振幅谱。