【C++】优先级队列

原创已于 2025-10-23 22:42:58 修改 · 749 阅读

28 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #算法

于 2025-08-08 14:35:19 首次发布

C++ 专栏收录该内容

19 篇文章

订阅专栏

priority_queue的介绍

优先级队列是一种容器适配器，其特性被设计为：按照某种严格的弱排序准则，其首元素始终是所包含元素中的最大值。
这种结构类似于堆（heap）的概念，允许随时插入新元素，但只能访问最大的堆元素（即优先队列顶部的元素）。
优先队列作为容器适配器实现，这些适配器类将特定容器类的封装对象作为底层容器，通过提供特定的成员函数集合来访问元素。元素从特定容器的"末端"弹出（此末端在优先队列中被称为顶部）。
底层容器可以是任何标准容器类模板，也可以是其他专门设计的容器类。该容器必须满足以下操作要求：

empty()（判空）
size()（获取大小）
front()（访问首元素）
push_back()（尾部插入）
pop_back()（尾部删除）

标准容器类vector和deque均满足这些要求。若未为特定priority_queue类实例指定容器类，则默认使用标准容器vector。
之所以要求支持随机访问迭代器，是为了能在内部始终保持堆结构。容器适配器通过自动调用算法函数make_heap、push_heap和pop_heap（在需要时）来维护这一结构。

priority_queue的使用

优先级队列默认使用vector作为其底层存储数据的容器，在vector上又使用了堆算法将vector中元素构造成堆的结构，因此priority_queue就是堆，所有需要用到堆的位置，都可以考虑使用priority_queue。注意：默认情况下priority_queue是大堆。

#include <vector>
#include <queue>
#include <functional> // greater算法的头文件
void TestPriorityQueue()
{
 // 默认情况下，创建的是大堆，其底层按照小于号比较
 vector<int> v{3,2,7,6,0,4,1,9,8,5};
 priority_queue<int> q1;
 for (auto& e : v)
 q1.push(e);
 cout << q1.top() << endl;
 // 如果要创建小堆，将第三个模板参数换成greater比较方式
 priority_queue<int, vector<int>, greater<int>> q2(v.begin(), v.end());
 cout << q2.top() << endl;
}

仿函数

在一个类中重载了（）运算符，使得该类的对象可以像函数一样使用，这就叫仿函数

class less
{
public:
    bool operator()(int x,int y)
    {
        return x < y; 
    }
}

int main()
{
    less lessfunc;
    lessfunc(1,2); // lessfunc.operator()(1,2)
    return 0;
}

仿函数的优点

1. 保持状态的能力

仿函数可以拥有成员变量，因此可以在多次调用之间保持状态，这是普通函数无法做到的。

cpp
class Counter {
    int count = 0;
public:
    int operator()() { return ++count; }
};

Counter c;
c(); // 返回1
c(); // 返回2
2. 作为参数传递时的优势

在STL算法中，仿函数比函数指针更灵活高效：

cpp
// 函数指针版本
void sort(vector<int>& v, bool (*comp)(int, int));

// 仿函数版本
template<typename Compare>
void sort(vector<int>& v, Compare comp);
3. 模板编程中的灵活性

仿函数可以作为模板参数传递，编译器可以进行更好的优化：

cpp
template<typename Func>
void process(Func f) {
    f(42);
}

struct MyFunctor {
    void operator()(int x) { /*...*/ }
};

process(MyFunctor());
4. 内联优化

仿函数的operator()通常可以被编译器内联，而函数指针则难以内联。

5. 多态行为

仿函数可以继承和组合，实现更复杂的行为：

cpp
template<typename Base>
class AddPrefix : public Base {
    string prefix;
public:
    AddPrefix(const string& p) : prefix(p) {}
    void operator()(const string& s) {
        Base::operator()(prefix + s);
    }
};

模拟实现

#pragma once
#include<vector>
#include<functional>
#include<stdbool.h>
#include<iostream>
using namespace std;
namespace program
{
    // 仿函数
    template <class T>
    class less
    {
    public:
        bool operator()(T a, T b)
        {
            return a < b;
        }
    };
    template <class T>
    class greater
    {
    public:
        bool operator()(T a, T b)
        {
            return a > b;
        }
    };
    template <class T, class Container = vector<T>, class Compare = less<T>>
    class priority_queue
    {
    public:
        priority_queue()
        {}
        void adjustdown(int parent)
        {
            int chlid = parent * 2 + 1;
            if (chlid + 1 < c.size() && comp(c[chlid],c[chlid + 1])) 
            chlid++;

            while (chlid < c.size())
            {
                if (comp(c[parent], c[chlid])) swap(c[parent], c[chlid]);
                else break;

                parent = chlid;
                chlid = parent * 2 + 1;
                
                if (chlid + 1 < c.size() && comp(c[chlid], c[chlid + 1])) 
                chlid++;
            }
        }

        void adjustup(int chlid)
        {
            int parent = (chlid - 1) / 2;

            while (chlid > 0)
            {
                if (comp(c[parent], c[chlid])) swap(c[parent], c[chlid]);
                else break;

                chlid = parent;
                parent = (chlid - 1) / 2;
            }
        }
        template <class InputIterator>


        priority_queue(InputIterator first, InputIterator last)
        {
            while (first != last)
            {
                c.push_back(*first);
                first++;
            }

            for (int i = (int)(c.size() - 1 - 1) / 2; i >= 0; i--)
            {
                adjustdown(i);
            }
        }

        bool empty() const
        {
            return c.empty();
        }

        size_t size() const
        {
            return c.size();
        }

        const T& top() const
        {
            return c.front();
        }

        void push(const T& x)
        {
            c.push_back(x);

            adjustup((int)c.size() - 1);
        }

        void pop()
        {
            if (!c.empty())
            {
                swap(c[0], c[c.size() - 1]);
                c.pop_back();
                adjustdown(0);
            }
        }

    private:
        Container c;
        Compare comp;
    };
    
};

应用

大小堆维护数据流的中位数

假设一些有序的数据流，小于中位数的元素被放到一个大根堆里面，大于中位数的元素被放到一个小根堆里面，并规定：大根堆的元素个数为 m，小根堆的元素个数为 n，大根堆的堆顶元素为下，小根堆的堆顶元素为 n，规定 m 和 n 一定要满足：要么 m == n，要么 m == n + 1。

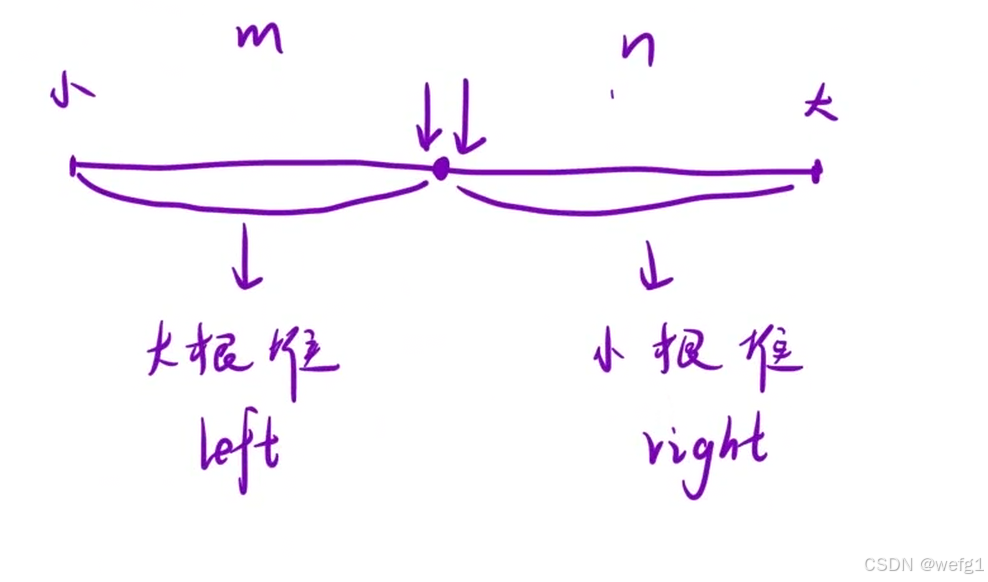
如果满足规定：这时要求数据流的中位数，如果 m == n，中位数 == （x + y）/ 2，如果 m == n + 1，中位数 == x。

任何插入元素保证以上规定：（分类讨论）

题目链接

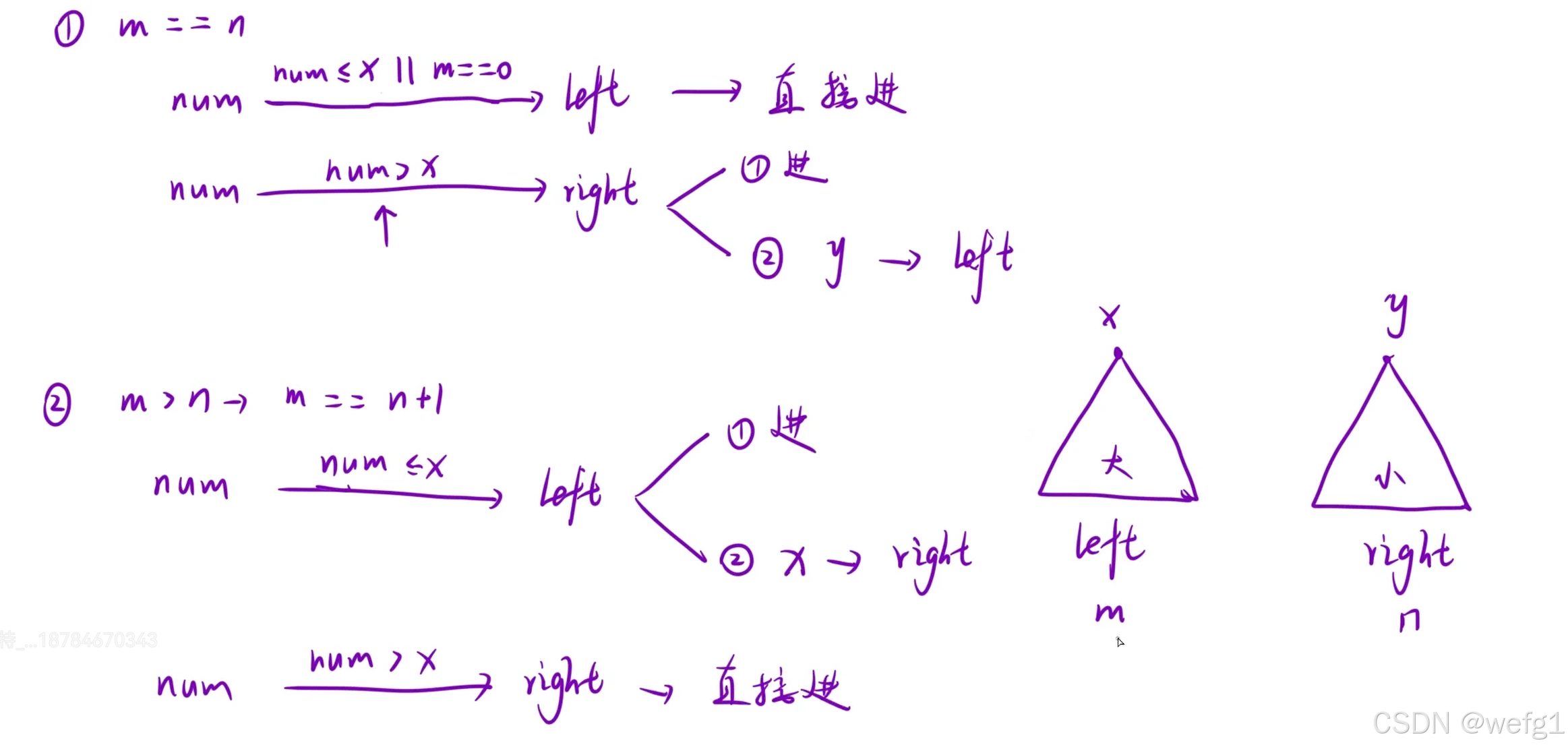
class MedianFinder {
public:
    MedianFinder() 
    {}
    
    void addNum(int num) {
        if(left.size() == right.size())
        {
            if(left.size() == 0 || num <= left.top()) left.push(num);
            else 
            {
                right.push(num);
                left.push(right.top());
                right.pop();
            }
    
        }
        else
        {
            if(num <= left.top())
            {
                left.push(num);
                right.push(left.top());
                left.pop();
            }
            else right.push(num);
        }
    }
    
    double findMedian() {
        if(left.size() == right.size()) return (left.top() + right.top()) / 2.0;
        
        return left.top();
    }

private:
    priority_queue<double> left;
    priority_queue<double,vector<double>,greater<double>> right;
};