目录
进制
进制也就是进位计数制,是人为定义的带进位的计数方法。

一、常见进制
二进制
基数为2,使用0和1两个数字来表示数。在计算机中,二进制被广泛应用,因为计算机的硬件电路可以很方便地表示0和1两种状态。
十进制
基数为10,使用0 1 2 3 4 5 6 7 8 9 这十个数字表示数。这是我们日常生活中最常用的进制。
十六进制
使用0到 9以及A 到F这十六个符号来表示数,其中A 到 F 分别表示10 11 12 13 14 15。十六进制常用于表示计算机内存地址等信息,因为它可以用较短的符号表示较大的数。
二、进制转换
十进制数 → R进制数
● 分整数和小数两部分处理:
● 整数部分:连续除以R,取余反序排列,直到商为0。
● 小数部分:连续乘以R,取整正序排列,直到乘积的小数部分为0,或者满足误差要求。
例如:
十进制数 13 转二进制
13 ÷ 2 = 6 ⋯ ⋯ 1
13÷2=6 ⋯⋯ 1
6 ÷ 2 = 3 ⋯ ⋯ 0
6÷2=3⋯⋯ 0
3 ÷ 2 = 1 ⋯ ⋯ 1
3÷2=1⋯⋯ 1
1 ÷ 2 = 0 ⋯ ⋯ 1
1÷2=0⋯⋯1 从下往上将余数排列得到1101,就是13的二进制表示。
十六进制转二进制:每一位十六进制数可以转换为4位二进制数。
例如,十六进制数2A,2转换为二进制是0010,A(即10)转换为二进制是1010,所以2A转换为二进制就是00101010。
二进制转十六进制:将二进制数从右到左每4位一组,分别转换为十六进制数。
例如,二进制数11011010,分组为1101和1010,1101转换为十六进制是D,1010转换为十六进制是A,所以11011010转换为十六进制是DA。
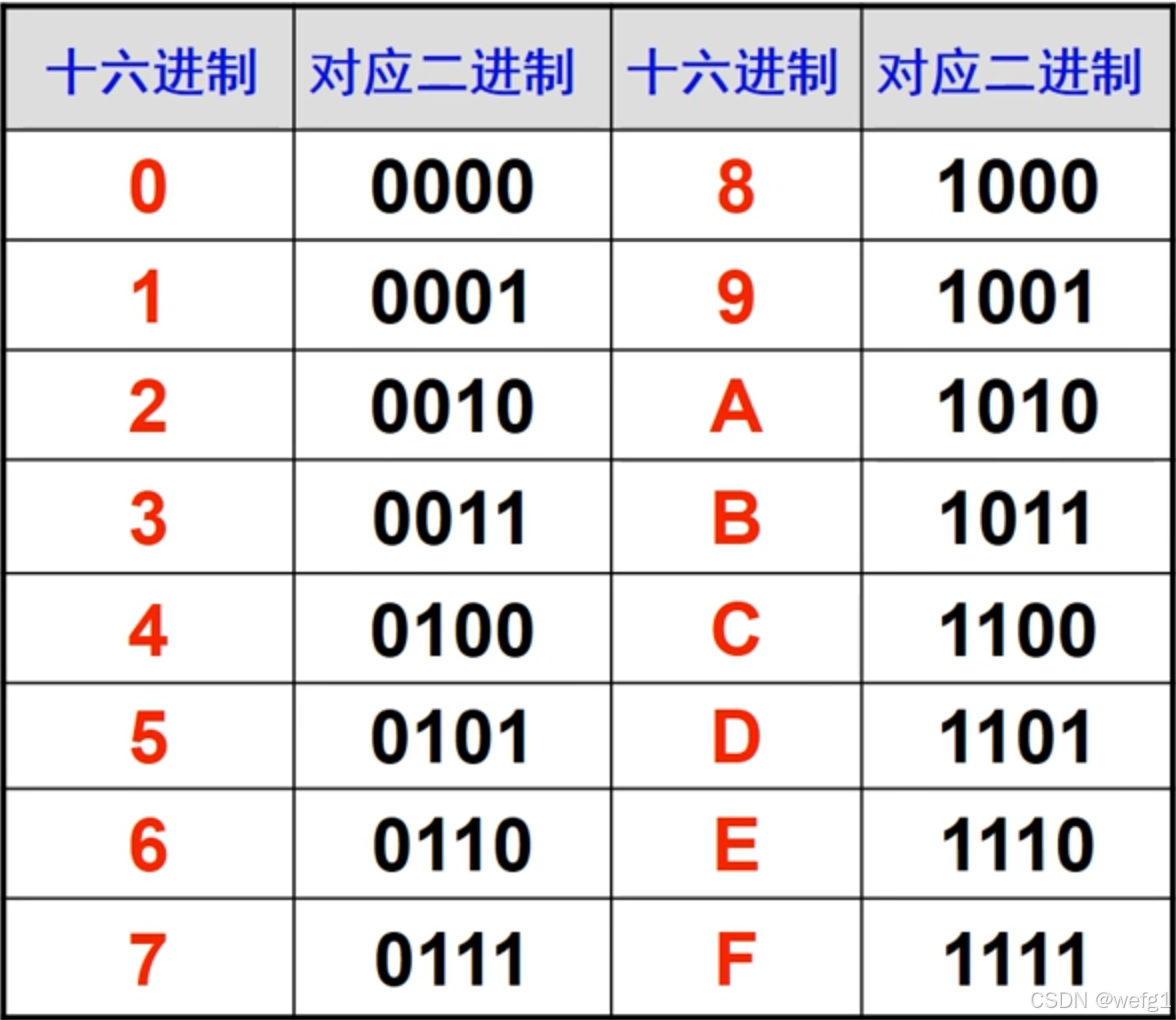
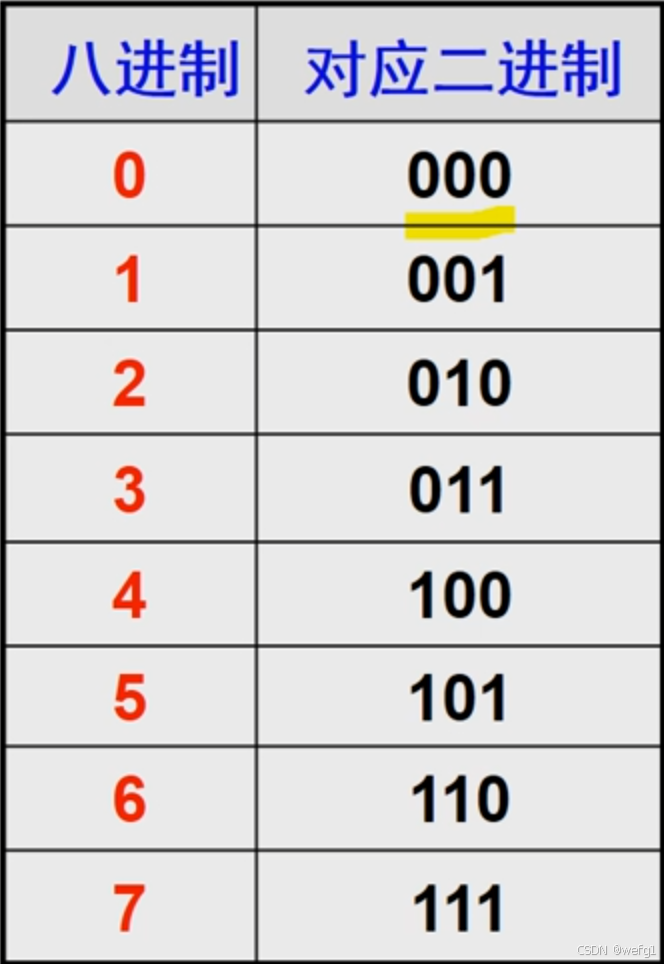
八进制与二进制互化方法与上述相似:
原码、反码与补码
计算机中的整数有三种2进制表示方法 , 即原码、反码和补码。
三种表示方法均有符号位和数值位两部分,符号位都是用 0 表示 “正” , 用 1 表示 “负”
正数的原码、反码、补码是相同的
负数的原码、反码、补码要经过计算的
原码
按照一个数的正负 , 直接写出它的二进制表示形式得到的就是原码
反码
反码是原码的符号位不变 , 其他位按位取反
补码
补码是反码+1
例:
整型占4个字节 (32bit)
如 10 的:
00000000000000000000000000001010 - 原码
00000000000000000000000000001010 - 反码
00000000000000000000000000001010 - 补码
-10 的
10000000000000000000000000001010 - 原码
111111111111111111111111111111110101 - 反码
111111111111111111111111111111110110 - 补码
原码、反码、补码的互相转化:
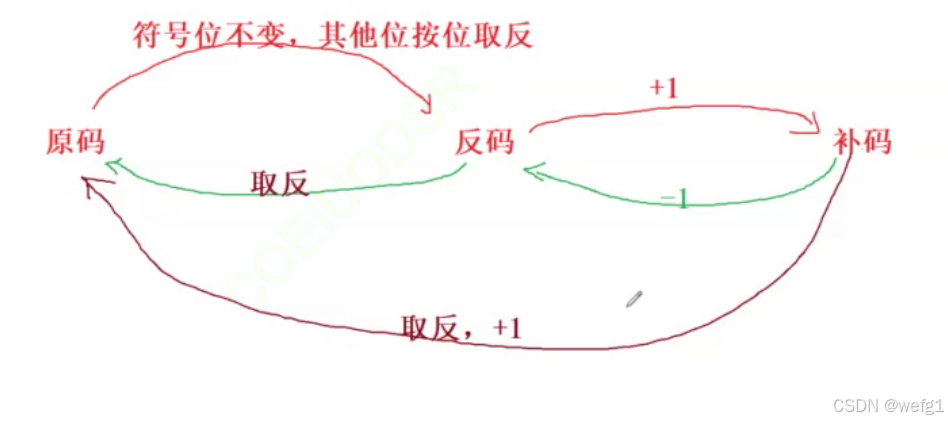
(取反:符号位不变 , 其他位按位取反,减去一不好得出结果时,也可以取反+1)
在计算机中,为什么要用用补码存储一个数呢?
在计算机系统中 , 数值一律用补码来表示和存储。原因在于,使用补码 , 可以将符号位和数值域统一处理 ; 同时 , 加法和减法也可以统一处理(CPU只有加法器)此外,补码与原码相互转换,其运算过程是相同的,不需要额外的硬件电路。
一个简单的例子:
如果计算机用原码存储一个数:
00000000 00000000 00000000 00000001 - 1 的原码
10000000 00000000 00000000 00000001 - 负1的原码
我们计算 1 - 1 就是 1 + (-1)
10000000 00000000 00000000 00000010 - 1 + (-1)的结果是 -2
这就出现问题了,结果显然不对。
如果我们使用补码
00000000 00000000 00000000 00000001 - 1 的补码
11111111 11111111 11111111 11111111 - 负1的补码
现在用 1 的补码和 -1 的补码相加:
1 00000000 00000000 00000000 00000000
由于整形占 4 个字节,所以最高位的那个 1 会溢出(截断),最终的结果是:
00000000 00000000 00000000 00000000
这样结果就正确了,所以计算机要用补码存储一个数。
移位操作符
左移操作符:b = a << m,作用:
a的补码左边丢弃m位,右边补m个零,然后作为b的补码赋值给b,a 的值没有变化。
右移操作符:b = a >> m,作用:
1、算术右移(大多数)
a的补码右边丢弃m位,左边补上原来的符号,然后作为b的补码赋值给b,a 的值没有变化。
(这个操作等价于将 a 除以 2 的 m 次幂,比如 a = a >> 1;等价于 a /= 2;)
2、逻辑右移(略)
左移操作符例子:
int a = 10; 10 的 补码:00000000000000000000000000001010
int b = a << 1; a << 1 : 00000000000000000000000000010100 — 值为 20 赋给 b
但 a 的值没有变化。
printf("%d",b)//打印出来的是原码
若a为负数,如:
int a = -10;
-10 的
10000000000000000000000000001010 - 原码
111111111111111111111111111111110101 - 反码
111111111111111111111111111111110110 - 补码
int b = a << 1;
a的补码左移一位,作为b的补码:
111111111111111111111111111111101100 - b的补码
由b的补码得到b的原码:
111111111111111111111111111111101100 - b的补码
111111111111111111111111111111101011 - b的反码
10000000000000000000000000010100 - b的原码
位操作符
按位与:c = a & b
作用:a 和 b 的补码中,对应位的二进制数有 0 则 c 的对应位为 0,都为 1 则 c 的对应位才为 1,
得到的结果作为 c 的补码。
一个神奇的表达式:
a = a & ( a - 1 );
这个表达式的作用:每执行一次,a 的二进制表示去掉最右边的一个 1,可以用来计算一个数的二进制表示中有多少个一。
(对于一个二进制数,减去 1 一定能将最右边的 1 所在的数位变成 0 ,如 0000000 1 减去 1 变成 0000000 0,000000 1 0 减去 1 变成 000000 0 1 ,再 “与上”减 1 之前的数,减 1 之前的数最右边的 1 对应的一定是 0)
十进制数中 2 的 k 次方的二进制表示只有若干 0 和一个 1。如
(十进制)2 =(二进制)00000010
(十进制)4 =(二进制)00000100
(十进制)8 =(二进制)00001000
利用这个性质,可以设计出一个检查一个数是不是 2 的 k 次方的代码,只需一条 If 语句搞定:
if (a & (a - 1) == 0)
按位或:c = a | b
作用:a 和 b 的补码中,对应位的二进制数有 1 则 c 的对应位为 1,都为 0 则 c 的对应位才为 0,
得到的结果作为 c 的补码。
按位异或:c = a ^ b
作用:a 和 b 的补码中,对应位的二进制数相同则 c 对应位为 0 ,不同则 c 对应位为 1 ,
得到的结果作为 c 的补码。
性质:1、a ^ a = 0
2、a ^ 0 = a
3、a ^ b ^ c = a ^ c ^ b ( 交换律 )
4、(a ^ b) ^ c = a ^ (c ^ b) (结合律)
应用举例:(不使用中间变量,交换两个变量的值)
int a = 5;
int b = 3;
a = a ^ b;----1
b = a ^ b;----2 把 1 式当作公式代入:b = a ^ b ^ a;而 a ^ b ^ a 等于 a
a = a ^ b; 把 2 式当作公式代入:a = a ^ a ^ b;而a ^ a ^ b 等于 b
其实这种方法效率不如使用中间变量,且可读性差,只能交换整数。也可以使用这种方法:
int a = 5;
int b = 3;
b = a + b;//可能会溢出
a = b - a;
b = b - a;
但若 a、b 都是很大的数字,则 b = a + b;这一步可能会溢出。
按位取反操作符
b = ~ a;
作用:将 a 的原码按位取反(包括符号位),然后作为 b 的补码赋给 b 。
如:
int a = 0,b = 0;
b = ~ a;
a 的:
原码:00000000000000000000000000000000
取反:1111111111111111111111111111111111111 —— 把它作为 b 的补码 ,b 的值为 -1 。
移位操作符、位操作符、按位取反操作符都是针对二进制数的运算符。
综合运用:
1、修改一个变量的 bit 位
想要修改一个变量的 bit 位,用指针是不行的,因为指针访问的是字节。
可以使用移位操作符、位操作符、按位取反操作符:
将一个数的二进制表示的第 x 位修改为 1:
a |= (1 << x);
将一个数的二进制表示的第 x 位修改为 0:
a &= ( ~ (1 << x) );
int main()
{
int a = 9;
//00000000000000000000000000001001
//00000000000000000000000000010000 1 << 4
//把a的二进制中第5位改成1
a |= (1 << 4);
//把a的二进制中的第5位改回来,变成0
//00000000000000000000000000011001
//11111111111111111111111111101111
//00000000000000000000000000001001
a &= (~(1 << 4));
return 0;
}
2、得到二进制任一位的数
( m >> i ) & 1
sizeof
sizeof 是既是操作符,也是关键字。
作用:计算并返回操作数的类型长度(以字节为单位,返回值的类型是 size_t ,这是专门为 sizeof 运算符创造的类型,它其实是 unsigned int 类型)
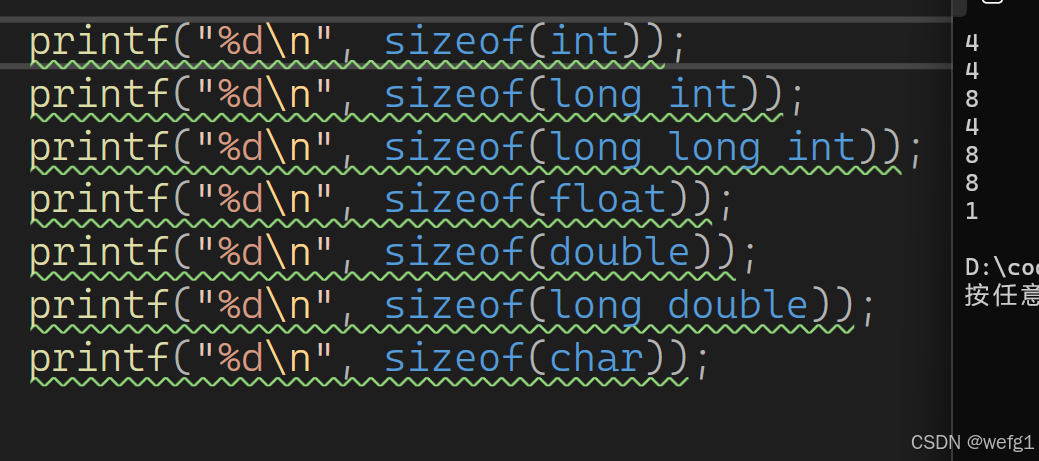
操作数可以是类型名、普通变量、数组名、数组元素等。
函数调用的时候要加( ),但 sizeof 可以不加 ,说明 sizeof 不是函数:

但是如果 sizeof 的操作数是类型名的时候,( )不能省略:
sizeof int -----错误
请分析以下代码:
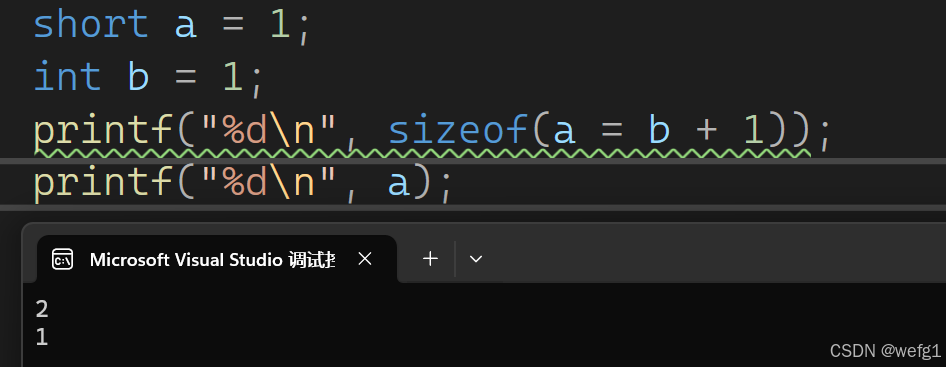
为什么 sizeof(a = b + 1) 这个表达式的值为 2 ?
sizeof(a = b + 1) 中明明已经将 b + 1 赋给了 a ,为什么 a 的值仍然是 1 ?
这是因为:
sizeof(a = b + 1) 中将整形数据赋值给短整形数据,结果为短整形
sizeof 在编译时已确定结果
sizeof(a = b + 1) 这条语句在编译时已确定为 2,在运行时相当于:
printf("%d\n", 2);
sizeof ( ) 括号内的表达式不计算
所以 a 的值依然是 1 。
字符串长度的求法:
1、strlen函数,如 char a[ ] = "abc" 则 strlen(a)= 3 , 不包括\0
2、sizeof操作符,如 char a[ ] = "abc" 则 sizeof(a)= 4 ,包括\0 ,
字符数组的最后一个元素的下标 = sizeof(a)/sizeof(a[0]) - 2
减去2是因为要减去 \0 和数组下标从0开始
sizeof 与数组:
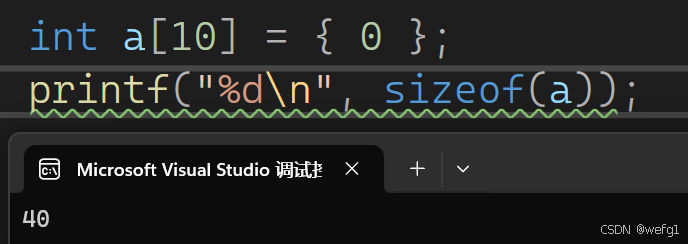
上图中,a 是数组名,a 数组有 10 个类型为 int 的元素, sizeof (a)计算的是数组的所有元素的类型所占字节的总和,也就是一个数组占用的字节数。
请分析以下代码:
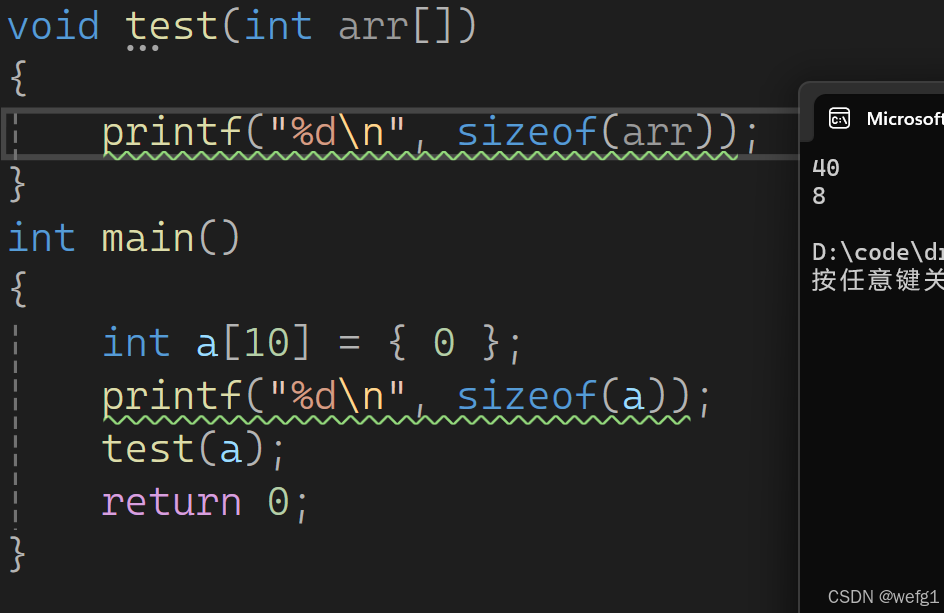
为什么 test 函数中 sizeof(arr) 的值是 8 呢?不应该是 40 吗?
这是因为:
数组传参传的是指针,即使形参写成数组的形式,本质上还是指针。
所以 arr 其实是指针变量,sizeof(arr) 计算的是指针变量 arr 所占的字节数,而不是数组所占的字节数。
数组的类型:
int arr[5]; int 是数组元素的类型, int [5] 才是数组的类型。
printf("%zd\n",sizeof(arr)); //输出5*sizeof(int)=20
printf("%zd\n",sizeof(int [5])); //输出5*sizeof(int)=20
数组名表示整个数组只有两种情况:
1. sizeof(数组名) , 数组名表示整个数组。计算的是整个数组的大小
只有数组名单独放在括号里才表示整个数组,若 a 是一维数组名,则:
sizeof(a+i),此时 a + i 表示 a[ i ] 这个数组元素的地址,只要是地址,它的大小就是 4 字节或 8 字节。所以 sizeof(a+i)这个表达式的结果就是 4 或 8。
sizeof(&a),&a 是整个数组的地址,只要是地址,它的大小就是 4 字节或 8 字节,所以 sizeof(a+i)这个表达式的结果就是 4 或 8。
sizeof(*&a)等价于 sizeof(a),这个表达式的结果是整个数组所占的字节数
2. &数组名 , 数组名表示整个数组。取出的是整个数组的地址
除此之外 , 所有的数组名都是数组首元素的地址
//一维数组
int a[ ] = { 1,2,3,4 };// 所占字节数 4*4=16
printf("%d\n", sizeof(a));//16
printf("%d\n", sizeof(a + 0));//a+0 其实是数组第一个元素的地址,是地址就是 4/8 字节
printf("%d\n", sizeof(*a));//*a是数组首元素,计算的是数组首元素的类型(int)大小,4
printf("%d\n", sizeof(a + 1));//a+1是第二个元素的地址 , 是地址大小就是 4/8
printf("%d\n", sizeof(a[1]));//a[1] 是第二个元素,计算的是第二个元素的类型(int)大小,4
printf("%d\n", sizeof(&a));//&a是整个数组的地址,整个数组的地址也是地址 , 地址的大小就是4/8字节//&a --- > 类型: int(*)[4]
printf("d\n", sizeof(*&a));//&a是数组的地址,*&a就是拿到了数组 , *&a -- > a , a就是数组名 , sizeof(*&a) -- >sizeof(a) /计算的是整个数组的大小,单位是字节 - 16
printf("d\n", sizeof(&a + 1));//&a是整个数组的地址 , &a+1,跳过整个数组 , 指向数组后边的空间 , 是一个地址 , 大小是4/8字节
printf("%d\n", sizeof(&a[0]));//&a[0]是首元素的地址 , 计算的是首元素地址的大小 , 4/8 字节
printf("%d\n", sizeof(&a[0] + 1));//&a[0] + 1是第二个元素的地址 , 地址的大小就是 4/8 字节
//字符数组
char arr[] = { 'a' , 'b' , 'c' , 'd' , 'e' , 'f' } ; \\ f 后面没有 \0
printf("%d\n", strlen(arr));//从‘a'开始找 \0 , 随机值printf("%d\n", strlen(arr + 0));//也是从‘a'开始找 \0,随机值
//printf("%d\n", strlen(*arr));//strlen('a')->strlen(97) , 非法访问(0x00 00 00 61 这个地址未分配,不能访问)-err
//printf("%d\n", strlen(arr[1]));// 'b' - 98 , 和上面的代码类似 , 是非法访问 - err
printf("%d\n", strlen(&arr));//&arr虽然是数组的地址 , 但是也是从数组起始位置开始找 \0 的 , 还是随机值
printf("%d\n", strlen(&arr +1)); //&arr是数组的地址 , &arr+1是跳过整个数组的地址,求字符串长度也是随机值
printf("%d\n", strlen(&arr[0] + 1));//&arr[0] + 1是第二个元素的地址,是 'b' 的地址 , 求字符串长度也是随机值
条件操作符
条件操作符,也称为三目操作符
通常的语法形式是:condition? expression1 : expression2 。
作用:如果condition为真(或满足某些条件),则计算并返回expression1的值;否则,计算并返回expression2的值。
逗号表达式
基本语法:使用逗号将两个或多个表达式分隔开,例如:expression1, expression2。
求值顺序:从左到右依次对每个表达式进行求值,整个逗号表达式的值是最后一个表达式的值。
应用场景:
for循环中的初始化和更新:例如:
for(int i = 0 , j = 10; i < j; i++ , j--) { // 循环体 }。
函数调用中的多个表达式:例如:
int a = 1 , b = 2;
printf( "%d\n" , ( a += 1 , b += 2 , a*b) ); // 输出 6。
赋值语句中的多个操作:
逗号表达式可以用于在单个赋值语句中执行多个操作。例如:
int x;
x = (1 , 2 , 3); // x的值为3。
隐式类型转换(整形提升)
C的整型算术运算总是至少以缺省(默认)整型类型的精度来进行的。
为了获得这个精度,表达式中的字符(1个字节)和短整型(两个字节)操作数在使用之前被转换为普通整型(int), 这种转换称为整型提升。
整型提升的意义:
表达式的整型运算要在CPU的相应运算器件内执行,CPU内整型运算器(ALU)的操作数的字节长度一般就是int的字节长度,同时也是CPU的通用寄存器的长度。
因此,即使两个char类型的相加,在CPU执行时实际上也要先转换为CPU内整型操作数的标准长度。通用CPU(general-purpose CPU)是难以直接实现两个8比特字节直接相加运算(虽然机器指令中可能有这种字节相加指令)。
所以,表达式中各种长度可能小于int长度的整型值,都必须先转换为int或unsigned int,然后才能送入CPU去执行运算。
例如:
char a = 1;
char b = 2;
char c = a + b;
a 和 b 的值被提升为整形,然后再执行加法运算。
加法运算完成之后,结果将被截断,然后存储于 c 中。
如何进行整形提升?
整形提升是按照变量的数据类型的符号位来提升的,有符号的数据类型整形提升时补码的高位补充符号位的数,无符号的数据类型整形提升时补码的高位补充0.
以 char 为例:
char c1 = - 1;
变量c1的二进制位(补码)中只有8个比特位:
11111111
因为 char 为有符号的 char 所以整形提升的时候 , 高位补充符号位 , 即为1
提升之后的结果是:
11111111111111111111111111111111
char c2 = 1;
变量c2的二进制位(补码)中只有8个比特位:
00000001
因为 char 为有符号的 char 所以整形提升的时候 , 高位补充符号位 , 即为0
提升之后的结果是:
00000000000000000000000000000001
//无符号整形提升,高位补0
分析以下代码:
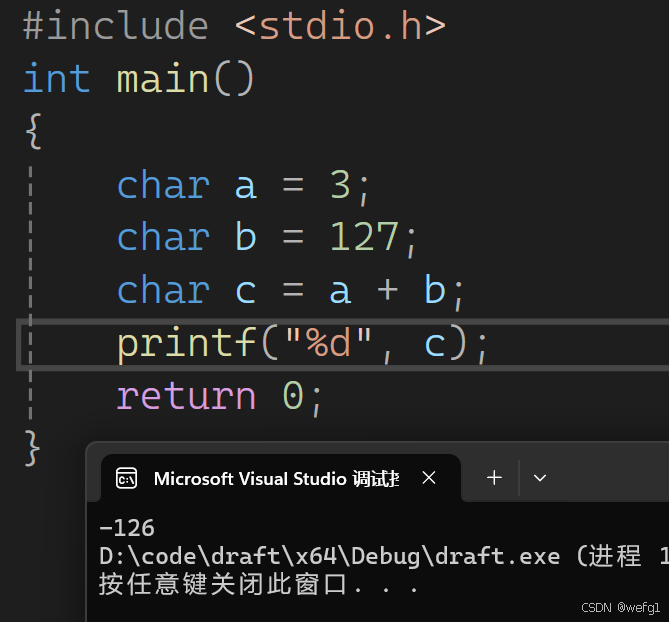
计算过程:
char a = 3 ;
3 的原码:00000000000000000000000000000011
由于 char 类型只占 1 个字节,所以将 3 存储到 a 时要发生截断,因此:
a 的补码:00000011(内存中以补码形式存储)
char b = 127;
b 的补码:01111111
char c = a + b;
要先对 a、b 进行整形提升:
a 整形提升后:00000000000000000000000000000011
b 整形提升后:00000000000000000000000001111111
a + b : 00000000000000000000000010000010
截断后存储到 c :
c 的补码:10000010(最高位是 1 ,c 已经是负数了)
printf("%d", c);
%d 是以有符号十进制整数形式打印二进制原码,所以要将 c 进行整形提升,再找到 c 的原码。
c 进行整形提升: 11111111111111111111111110000010
取反+1得到原码:100000000000000000000001111110 (这是 -126 的原码)
所以打印的是 -126 。
有符号的 char 类型(signed char)的取值范围是 -128 到 127 ,如何得来的?
signed char 类型占 1 个字节即 8 bit ,1 个 bit 有 0 或者 1 两种可能,8 个 bit 可以有 2 的 8 次方即 256 种组合,可以表示十进制的0 到 257,但最高位为符号位,即表示数值实际有 7 个 bit 位(128 种组合),当最高位为 0 (表示正数)时可以表示十进制的 0 到 127 ,当最高位为 1 (表示负数)时可以表示十进制的 -128(10000000 规定为 -128) 到 -1 (11111111),所以,有符号的 char 类型(signed char)的取值范围是 -128 到 127 。其他类型,如 int 类型可以依此类推。
对于 unsigned char (无符号字符型)最高位不再表示符号,此时 8 个 bit 位都表示数值,所以 unsigned char 的取值范围是 0 到 255 ,其他类型,如 unsigned int 类型也可以依此类推。
char a = 127;(a:01111111)此时对 a 加一,(a + 1:10000000,这个二进制数规定为 -128)a 的值为 -128,再对 a 加一,(a + 2:10000001,-127)a 的值为 -127,一直对 a 加一,a 的值会从 -127 到 -126 ... 一直到 -1(11111111)再加一(100000000,1 溢出,a 的值变为00000000,即0)a 的值变为 0。
所以说,对一个 char 类型的数无休止的加一,这个数不会一直增加,它的值呈现为在一定范围内周期性的变化。
请分析以下代码:

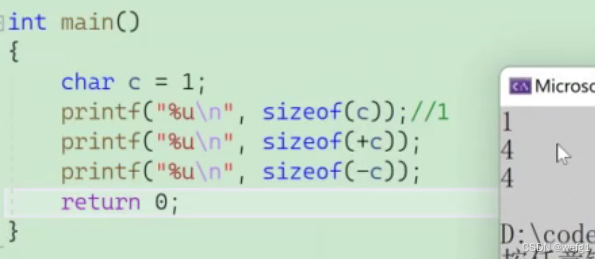
最后只打印出了 c ,请思考为什么
(tip:0xb6 表示十六进制数字 b6 ,二进制形式为10110110,十六进制数字每一位占半个个字节, ==运算有时也要整形提升 )
下面这个例子也说明了整形提升的存在:( “+”也是操作符,对 c 要整形提升)
算术转换
C语言中的算术转换是指在执行算术运算时,操作数的类型会被自动转换为一种公共类型,以确保运算的正确性。这种转换通常发生在二元运算符(如 +、-、*、/ 等)的操作数之间。

如果某个操作数的类型在上面这个列表中排名较低 , 那么首先要转换为另外一个操作数的类型后执行运算。
如:
int a = 1;
foalt b = 3.14f ;
a + b ;
在执行 a + b 时,会把 a 转换为 float 类型,再进行相加。
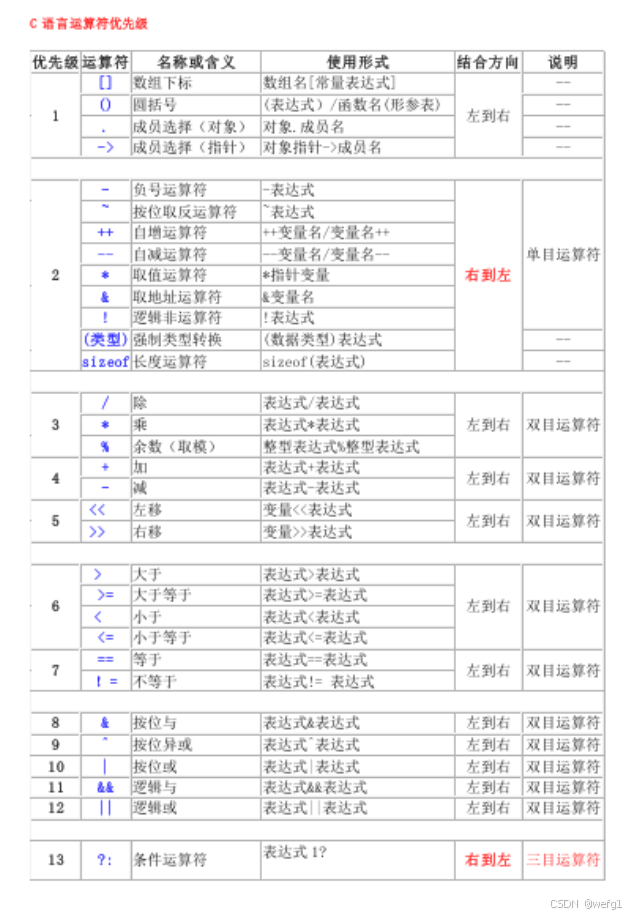
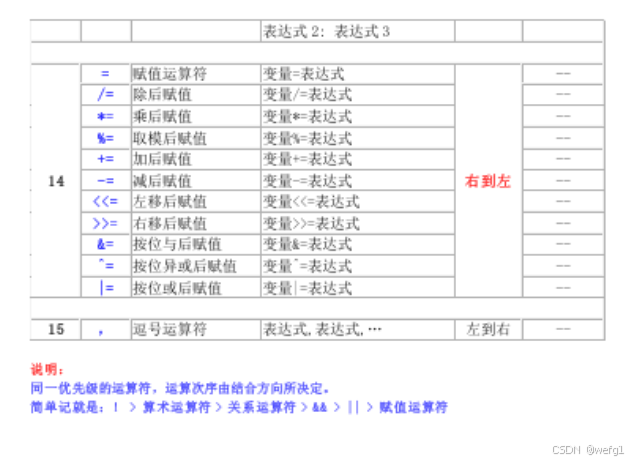
操作符的优先级、结合性
总结:
下标圆括号成员选择 > 单目运算符 > 算术运算符 > 位移运算符 > 关系运算符 > 按位运算符 > 逻辑运算符 > 三目运算符 > 赋值运算符 > 逗号运算符
当多种操作符在一个表达式时:
首先确定优先级,相邻操作符按照优先级高低计算 ,优先级相同的情况下,结合性才起作用。
有些表达式的计算路径不是唯一确定的,这种表达式容易出 BUG ,称为问题表达式
比如:
例1
a*b + c*d + e*f ; 1 3 2 5 4 ----计算顺序1 1 4 2 5 3 ----计算顺序2
如果 a*b 的结果影响 c*d 的结果,那么就容易出现BUG
例2
int fun()
{
static int count = 1;
return ++count;
}
int main()
{
int a = fun() - fun() * fun() //这里可能会出现BUG,
//因为你不知道编译器会先调用 - 号前面的 fun()还是 * 前面的 fun()
return 0;
}
例3
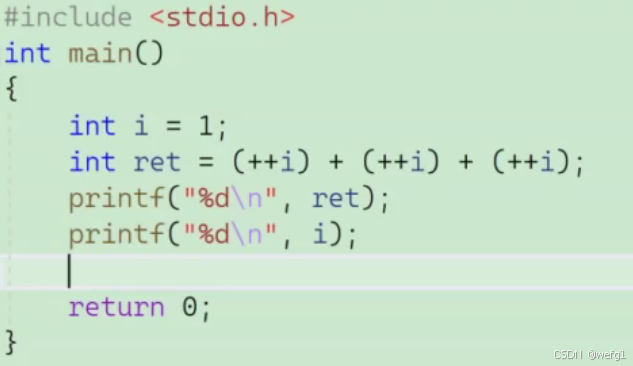
可以在不同的编译器运行以上代码,ret 的结果可能不同。





















 1787
1787

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








