神经网络优化之优化器

最新推荐文章于 2024-11-28 17:14:03 发布

原创最新推荐文章于 2024-11-28 17:14:03 发布 · 1.2k 阅读

3 ·

CC 4.0 BY-SA版权

文章标签：

#Tensorflow优化器 #Tensorflow优化方法 #梯度下降法 #批量梯度下降法 #随机梯度下降法

深度学习专栏收录该内容

13 篇文章

订阅专栏

本文深入探讨了梯度下降算法与反向传播在神经网络训练中的应用，对比了批量梯度下降(BGD)与随机梯度下降(SGD)的优缺点，介绍了Tensorflow中的多种优化器，如Adadelta、Adagrad、Momentum、Adam等，并通过实例展示了如何使用Tensorflow实现神经网络的训练。

基本概念

梯度下降算法主要用于优化单个参数的取值，而反向传播算法给出了一个高效的方式在所有参数上使用梯度下降算法，从而使神经网络模型在训练数据上的损失函数尽可能小。需要注意的是，梯度下降法并不能保证被优化的函数达到全局最优解。只有当损失函数为凸函数时，梯度下降法才能保证全局最优解。
Tensorflow提供了很多优化器（optimizer），我们重点介绍下面8个

tf.train.GradientDescentOptimizer
tf.train.AdadeltaOptimizer
tf.train.AdagradOptimizer
tf.train.AdagradDAOptimizer
tf.train.MomentumOptimizer
tf.train.AdamOptimizer
tf.train.FtrlOptimizer
tf.train.RMSPropOptimizer

这8个优化器对应8种优化方法，分别是梯度下降法（BGD和SGD）、Adadelat法、Adagrad法（Adagrad和AdagradDAO）、Momentum法（Momentum和Nesterov Momentum）、Adam法、Ftrl法和RMSProp法，其中BGD、SGD、Momentum和Nesterov Momentum是手动指定学习率的，其余算法能够自动调节学习率。

BGD法

BGD的全称是Batch Gradient Descent，即批梯度下降。这种方法是利用现有参数对训练集中的每一个输入生成一个估计输出_yi，然后跟实际输出yi比较，统计所有误差，将平均误差作为更新参数的依据。这种方法的优点是，使用所有训练数据计算，能够保证收敛，并且不需要逐渐减少学习率；缺点是，每一步都需要使用所有的训练数据，随着训练的进行，速度会越来越慢。

import tensorflow as tf
from numpy.random import RandomState

#定义神经网络的参数,随机初始化
w1 = tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))
w2 = tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))
#在shape上的一个维度上使用None可以方便使用不同的batch大小
x = tf.placeholder(tf.float32, shape=(None, 2), name='x-input')
y_ = tf.placeholder(tf.float32, shape=(None, 1), name='y-input')
#定义神经网络前向传播的过程
a = tf.matmul(x, w1)
y = tf.matmul(a, w2)
y = tf.sigmoid(y)
#定义损失函数:交叉熵
cross_entropy = -tf.reduce_mean(y_ * tf.log(tf.clip_by_value(y, 1e-10, 1.0))
     +(1-y_) * tf.log(tf.clip_by_value(1 - y, 1e-10, 1.0)))
#反向传播算法应用
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(cross_entropy)

#通过随机数生成一个数据集
rdm = RandomState(1)
dataset_size = 128
X = rdm.rand(dataset_size, 2)
#认为x1+x2<1的样本都认为是正样本，用0表示负样本，1来表示正样本
Y = [[int(x1+x2 < 1)] for (x1, x2) in X]

with tf.Session() as sess:
    #初始化变量
    init = tf.global_variables_initializer()
    sess.run(init)
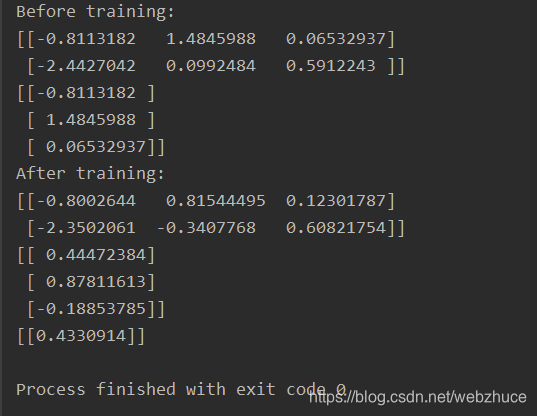
    print("Before training:")
    print(sess.run(w1))
    print(sess.run(w2))
    #设定训练的次数
    STEPS = 5000
    for i in range(STEPS):
        #通过样本集训练神经网络并更新参数
        sess.run(train_step, feed_dict={x: X, y_: Y})

    print("After training:")
    print(sess.run(w1))
    print(sess.run(w2))
    result = sess.run(y, feed_dict={x: [[0.5, 0.3]]})
    print(result)

运行结果

在这里插入图片描述

SGD法

SGD的全称是Stochastic Gradient Descent，即随机梯度下降。因为这种方法的主要思想是将训练数据集拆分成一个个批次(batch)，随机抽取一个批次来计算并更新参数，所以也称为MBGD(Mini Batch Gradient Descent)。SGD在每一次迭代计算mini-batch的梯度，然后对参数进行更新。与BGD相比，SGD在训练数据集很大时，仍能以较快的速度收敛。但是，它仍然会有下面两个缺点。
1、由于抽取不可避免地梯度会有误差，需要手动调整学习率，但是选择合适的学习率有比较困难。
2、SGD容易收敛到局部最优，并且在某些情况下可能被困在鞍点。

#设定训练的次数
STEPS = 5000
for i in range(STEPS):
    #每次选取batch_size个样本进行训练
    start = (i * batch_size) % dataset_size
    end = min(start + batch_size, dataset_size)
    #通过选取的样本训练神经网络并更新参数
    sess.run(train_step, feed_dict={x: X[start:end], y_: Y[start:end]})