线性代数学习之行列式

行列式：

什么是行列式？

继续接着线性代数学习之坐标转换和线性变换往下学习，这次则来学习行列式相关的知识，其实很多线性代数教材都是一开始从行列式开始学习， 而咱们的学习并不是这样的，这是因为行列式和矩阵以及空间的基等概念有密切的联系，而很多国内的教材都比较注重行列式的具体计算，但是呢这里重点不是关注它的计算，而关注它的性质，了解清楚它的本质【你了解了本质再去看它的计算也会非常的容易】，为后续特征值与特征向量的学习打下非常坚实的基础。

回到正题上来，什么是行列式呢？一句话来描述：行列式是方阵的一个属性，类似的：

1、我们在研究一个数时也会涉及到属性：数的大小、符号、约数、是否是素数？

2、研究角度时也有属性：sin、cos、tan、ctg...

3、研究多项式：
 

它也有一些属性值得研究，如项数、次数、多项式=0的解。

那行列式到底是方阵的一个什么属性呢？在之前的学习中我们知道“矩阵可以表示一组向量，方阵表示n个n维向量”，也就是把向量一列列的组合起来形成了矩阵，可以表示一个空间及这空间中的一组基所对应的坐标转换，同理方阵就可以理解成n个n维向量，还是拿二维平面空间来说，使用2个二维向量就可以作为空间中的一组基，就可以描述这个空间，也就是空间中的任何一个向量都可以被这两个二维向量线性表示出来，下面来看这样两个标准基：

很显然可以表达一个二维空间，那如果这样两个绿色的向量呢？

当然也可以表示一个二维平面，同样的再来两个蓝色的向量：

那能否用一个数字表示这些向量组的不同呢？其实是可以的，每2个向量都组成了一个面积，比如单位向量组成了红色面积：

而绿色的两个向量就组成了绿色的面积，如：

而对于蓝色的向量组成的是一个虚线部分的面积：

而这些面积的大小就能一定程度的刻画不同的基它们的一个特征，而行列式就是描述这个n个n维向量它所对应的面积的大小这样的一个属性，当然这里说面积是针对二维平面来说的，如果对于一个三维平面空间就要有三个三维向量，如下：

它表示的是一个体，而非面啦，很显然三个三维向量不同则表达的体积也会不同，比如像这个：

再往高维去看就很抽象了，比如四维、五维...，都能找到n个n维空间所构成的体，而行列式就是描述的这个n个n维向量所构成的n维体所对应的体积，当然在二维空间中就是面积了。

如何求行列式？

还是以二维平面来例，比如有这么两个向量：

而它的行列式表示法是这样的：

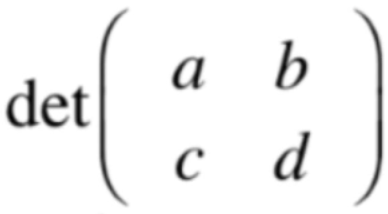
其中det是行列式英文Determinant的缩写，而且它一定是方阵，另外它里面是把向量以行来进行排列的，其实学到后面对于行列式的矩阵表示以行还是以列其实都是一样的，之后再说，目前用行进行排列，另外行列式不是行写在前面嘛，所以也可以这么理解，另外对于行列式还可以这样表示：

看到它是不是跟一个数的绝对值符号一模一样？是的，所以对于数学当中要区分双竖线里面的数据是什么类型，如果它是一个矩阵那就是在求这个矩阵的行列式，它的值也是一个数，不过它跟绝对值不一样的是有可能是一个负数，接下来看一下对于这么一个行列式要怎么求它的值呢？其实就是求图中平行四边行的面积，看下面：

先来将向量的坐标值标出来：

然后再在平行四边行最远的一点分别向x,y划辅助线：

其实要求平行四边行的面积就是用整个这个长方型的面积减掉它周边块的面积就可以了，为了求出此时还得画辅助线：

具体计算就不过多解释了，比较简单，整个式子为：

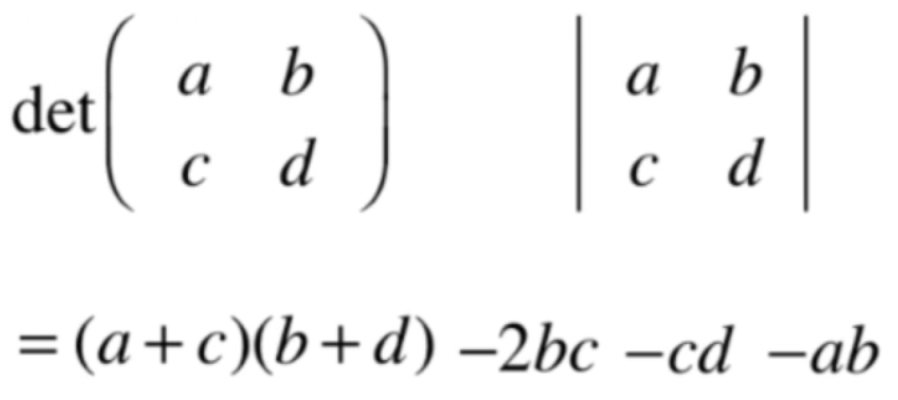
此时就可以化为：

所以对于二维行列式的求解结果为：

其中发现规律没有？其实就是矩阵的主对角线两个元素（a、d）的乘积减去非主对角线两个元素(b、c)的乘积，但是！！！这种规律只适合二阶方阵，如果是三阶行列式的求法就不能用这种方式了，关于更多阶行列式的求法在后面会来学到，目前先只看二阶的。

接下来做一个变换，来寻找一些特性：将行列式的两行交换一下位置就有：

有啥意义么？这两个行列式是不是有这么一个关系：

就能说明：行列式表示向量组在空间中形成的有向【有向的含义是求出来的值有可能是正，也有可能是负的】体积【二维空间叫面积】，其中在二维空间中的有向面积还是很容易直观理解的，看图说话：

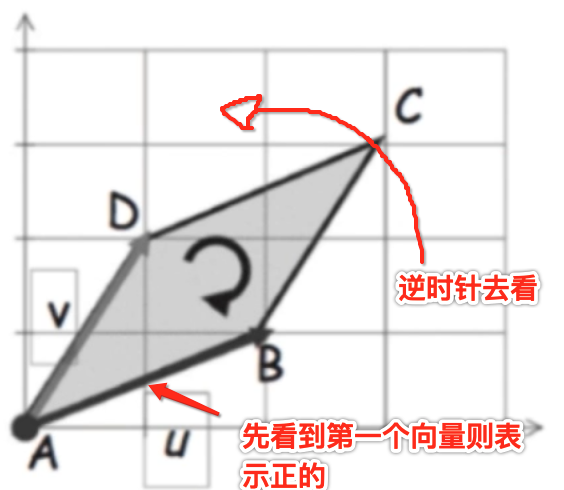
但是！！！在三维及以上的空间中，体积的方向将变得极其复杂，但是可以简单总结如下性质，高维的也一样满足：

在行列式中，向量排列的顺序是有意义的。交换两行，则行列式的值取反。

行列式的四大基本性质：

了解了行列式之后，接下来则从更加抽象的层面出发来来看行列式的四大基本性质：