多跳能量共享方案研究

可充电无线传感器网络中的多跳能量共享

1 引言

近年来，一种旨在延长网络寿命的新技术——能量共享， 正受到越来越多的研究关注。为了实现无线传感器网络 （WSN）的长期运行，缓解能量受限问题的经典方法 大致可分为两类：能量节约和额外能量补充。前者主要 通过设计能量感知协议或平台/硬件来实现，而后者则指 通过更换电池或利用附加模块采集自然资源，如太阳能 板（Park 和 Chou，2006）以及风能或振动能量发电 机。能量采集技术可通过额外的能量补充支持网络永久 运行。但由于某些环境因素（如云层遮挡），导致节点 获得的采集能量分布不同且随时间变化，因此能量采集 可能加剧节点间的能量不平衡。另一种方法是使用无线 充电车为低能量节点充电（Shi 等，2011）。无线传感 器网络可能部署在野外应用场景中（Xiao 等，2006； Mo 等，2009；Mainwaring 等，2002），在这种情 况下，更换电池成本高昂，或难以通过移动充电器为节 点充电。上述两类传统方法均面临一个严重问题，即节 点间的能量不平衡，这会导致能量效率低下和网络寿命 缩短（Lan 和 Yang，2006）。本文关注一种新技术—— 能量共享，它可作为缓解网络中能量不平衡问题的一种 替代方案，尤其是在节点能够采集自然资源的情况下 （Zhu 等，2010）。近年来，能量共享技术在无线传感 器网络中的研究与应用日益增多（Zhu 等，2010；Li 等，2010；Peng 等，2010；Tong 等，2010；Shi 等， 2011），因为它对一些应用具有潜在益处，例如可穿戴 计算（Yun 等，2008）、绿色建筑（Jiang 等，2009） 等。大多数现有能量共享研究通过移动充电器传输能量， 并试图为其寻找最优路径。这些能量共享方法实际上是 点对点的，与射频识别（RFID）系统中的方式并无本 质区别（Xiao 等，2007）。在RFID系统的能量充电过 程中，潜在的能量接收器必须是无源RFID标签，而能 量源则必须是拥有充足能量的读取器（海因里希和皮莱， 2005）。与以往的能量共享方案不同，本文提出一种新 颖的方式——多跳能量共享，在无需移动充电器的情况 下实现节点之间的能量共享。

多跳能量共享

这种新型方案——多跳能量共享，具有 多跳能量传输的内在特性，与以往的方案不同。多跳能 量共享的基本思想是，能量可以像数据一样对待，因此 可以在网络中像数据包一样进行传输（Zhu 等，2010； Liu 等，2006年）。但由于能量共享过程中的物理特性， 多跳能量共享在某些方面不同于数据传输。首先，多跳 能量共享的干扰模型与无线通信干扰模型完全不同。例 如，在大多数用于无线通信的干扰模型中，干扰范围被 建模为圆形或模拟形式。无线通信期间，电磁覆盖在无线能量充电过程中完全不同。在无线通信中，当接收器受到干扰时无法接收数据。有趣 的是，由于其他节点之间的能量共享导致的能量耗散，附 近的接收器可能会意外地被充入一些能量。其次，能量必 须从具有较高能量水平的节点流向较低能量水平的节点， 这是能量充电过程中的固有物理特性。在数据传输过程中， 只要节点有足够的能量来接收或发送数据，其作为接收器 或发射器的能力不会仅因其能量水平而受到影响。第三， 与采用无源标签的射频识别系统中的能量充电不同，在射 频识别系统中可能的能量接收器必须是射频识别标签，而 能量源必须是具有丰富能源的读取器（海因里希和皮莱， 2005；穆斯塔法等，2012），多跳能量共享则允许任何节 点都可能成为源节点或目标节点，或者能够为其他节点中 继能量。

这些特点表明，尽管朱等人（2010）认为能量可以 像数据一样传输，但用于数据传输的协议并不能直接应 用于多跳能量共享。此外，在能量收集无线传感器网络 中，能够比其他节点收集更多资源的节点，应承担更多 任务或与其它节点共享其能量。否则，由于节点电池的 有限容量，采集能量将过度累积而被浪费。朱等人（ 2010）设计了一个由能量路由器及相关能量接入和网络 协议组成的硬件平台，以在嵌入式传感器设备之间高效 且定量地路由能量。该设备证明了通过多跳模式在节点 间共享能量是可行的。上述事实促使我们开发一种新型 多跳能量共享方案（MESS），并设计相应的算法来实 现该方案。

本文的贡献

基于日益受到研究和应用的能量共享技术， 本文提出了一种新颖的多跳能量共享方案(MESS)，以 实现节点间在多跳模式下的能量共享。据我们所知，本 文是首次分析多跳模式下能量共享的研究。本文首次提 出了可行的多跳能量共享路径的条件。不同于直接设计 寻找多跳能量共享路径的方案，本文设计了另一种相对 更易于实现的方案，称为MESS。在MESS中，本文分 别针对静态和动态能量共享两种情况设计了算法： SESA和DESA。在第一种情况下，能量共享过程中没 有其他消耗能量的动作发生，因此每个节点的剩余能量 为静态，其变化仅由能量共享引起。例如，节点在夜间 无法进行太阳能能量收集，且各节点除能量共享外不执 行任何任务。在第二种情况下，每个节点的剩余能量为 动态，可能由于能量收集、任务执行以及其他节点能量 共享的影响等因素而发生变化。针对这两种情况，我们 的算法考虑了能量共享的两个对立方面：奖励与共享能 量的成本。我们的算法在能量成本受限的同时，几乎最 优地实现了最大化网络收益。本文的主要贡献如下。

设计了一种近乎最优的方案，用于无线传感器网络中 的多跳能量共享。该方案考虑了静态和动态两种情况， 并分别针对这两种情况提出了两个算法： SESA和 DESA。我们的理论分析表明，无论是 SESA还是 DESA，其总奖励至少达到最优方案的 1 − 1/e。在 动态情况下，DESA所获得奖励的期望误差可以为 E (∆τ)，其中 ∆τ。由于能量共享带来的能量消耗也在 MESS中被这两个算法所限制。

2 系统模型

本节阐述了网络、功耗和奖励模型。

假设有 n个传感器节点组成一个集合 V={v1, v2,…, vn}，构成一个网络。该网络的节点密 度必须足够高，以确保每个节点能够将其能量传输给至 少一个邻居。每个节点都配备了能够

• 从环境中采集自然资源
• 与其他节点共享能量。

假设共享能量的模块可以调整其角度至合适的方向，从 而能够高效地向接收器传输能量。每个节点还具有容量 受限组件，例如可充电电池或电容，用于存储能量。每 个节点的最大容量用 B表示。对于每个节点，始终存在 约束 0 ≤ E m i(τ) ≤ B，其中 E m i(τ)表示节点 v i在时 隙 τ开始时的剩余能量。 E m i(τ)包含几个部分：前一时 隙的剩余能量、消耗能量、获取能量、传输能量和接收 能量，分别表示为E m i(τ − 1)、 E c i(τ − 1)、 E h i(τ − 1)、 E t i( τ − 1)和 E r i(τ −1)。这里， E t i( τ − 1)表示 v i 传输给 其他节点的能量，包括传输到目标节点途中的能量消耗， 即 E c i(τ)。实际上，与能量存储装置（如AA型电池）的 容量相比，该消耗能量非常小。本文中大多数符号及其 含义见表1。

符号	含义
f	奖励函数
E	能量
vi	节点ID
θij	vi到 vj的能量共享动作
τ	时隙
S	动作集合
c	能量共享成本
X	源节点集合
R	目标节点集合
k	X 的基数
Ni	vi的最大邻域 能量共享范围

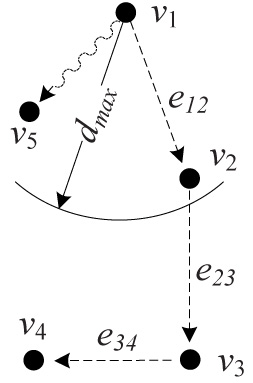
在能量共享过程中，根据Kurs 等人 (2007) 的研究成果， 部分能量不可避免地被消耗和耗散。尽管能量共享引起 的功耗与多个参数相关，但由于能量收发装置的大多数 参数是固定的，因此主要由源节点与其目标之间的距离 决定。设 dij表示节点 vi与 vj之间的距离。当节点 vi 向 vj传输能量时，在距离 dij上的能量消耗为 cij= αdβij， 其中 α和 β为正数常量。令 dmax表示一个节点 vi可 将其能量传输至其一跳邻域的最大距离，因此它具有最 大的邻域 Ni。在能量共享过程中，能量耗散是一种物 理现象，可能导致无线能量共享中的主要能量损失。能 量耗散还会导致节点将部分能量传输到意外目的地。例 如，在图1中，当节点 v1向节点 v2传输能量时，会将部 分能量耗散到节点 v5。本文不要求了解能量收集和耗散 的分布模型。同时，每个节点也能够获取能量。根据第 6节中给出的相关工作，在每个时隙（如一小时）内采 集的能量量值也远小于能量存储设备的容量。

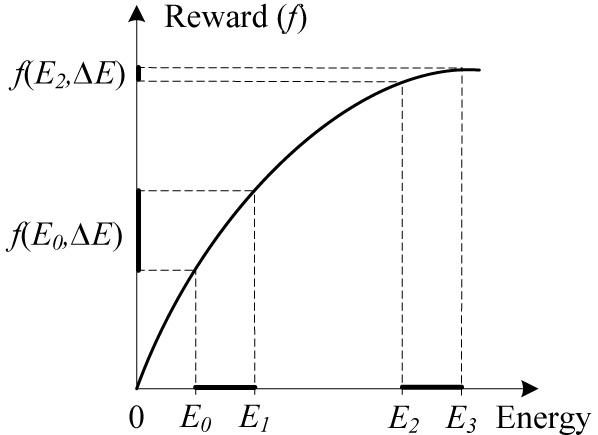
本文引入了能量共享动作这一概念，并用 θ表示。采取一 个动作意味着一个发射器向接收器传输一定的能量。同时 引入了一个奖励函数来衡量一个动作所获得的奖励。每个 动作的奖励 f是接收器的剩余能量 E r和共享能量 ∆E的 函数，并将此函数称为奖励函数，即 f(E r ,∆E)。当一个 动作 θij 时，即 vj 从节点 vi接收一定量 ∆E 的能量，该动作会获得某种奖励，记为f(θij)。注意，在 动作 θij 中，两个节点 vi 和 vj 是相邻的。因此，我们有 f(θij) = f({v13,∆E)。奖励函数的公式取决于具 体应用，以往的研究设计了不同的函数来描述网络在传 感器激活（任等人，2012）、覆盖范围（唐等人，无日 期；肖等人，2010）等方面所能获得的奖励。许多先前 的工作假设奖励函数是非递减、单调且凸的。直观上讲， 承担更多任务的节点相比其他节点剩余能量更少，因此 比其他节点更迫切需要能量。本文假设接收器 vi 的奖 励函数 fi 是单调且凸的，如图2所示。接收器的剩余 能量和共享能量都会影响动作的奖励。例如，在两个不 同时间点分别执行两个动作，此时 vj 的剩余能量分别为 E0 和 E2。尽管在这两种情况下 vj 接收的能量总量都等于 ∆E，其中 ∆E= E1 − E0=E3 − E2，显然 f({v27,∆E) > f({v32,∆E)，因为 E0<E2 且 vj 在 E0 点比在 E2 点更急需能量。本文还假设奖励函数是 非递减、单调且凸的。

请注意，一个动作 θij会消耗发射器 vi的一些能量，这部分能量包括两个部分：一部分被其接收器 v j接收到，另一 部分在从 vi到 v j 的传输过程中耗散。前者通过目标节点返 回并获得一定的奖励，而后者在能量共享过程中被浪费。 我们将后一部分称为动作 θi j 的成本。当采用一种能量共享 方案时，我们总是希望该方案消耗的能量尽可能少。因此， 方案的成本是评估其性能的另一个重要指标。

在多跳网络中，总奖励函数表示为 fV，即 fV =∑v j ∈ R fj ，其中 fi是节点 vi的奖励函数， i= 1, 2,…, n。假设 fV在本文其余部分是对称的，并且如之 前假设所述，也是非递减的、单调的和凸的。在本文接 下来的内容中， S表示一组动作，该组动作的总奖励记 为 f(S)，即 f(S) =∑ fθ∈ S(θ)。

3 问题表述与可行解

3.1 问题表述

该模块将能量共享问题形式化如下：在每个时隙 τ ∈ T，选择 一个源节点集合。这些源节点分别找到其目标节点，目标节点可能是多跳距 离。每个源节点 vi通过中继节点逐跳将其能量传输到其目 标节点。这样，在每个源节点与其目标节点之间形成一条 能量共享路径。这意味着每条能量共享路径由若干动作组 成。在每个时隙 τ，有多个动作完成。这些动作的发射器和 接收器节点构成两个集合 Xτ和 Rτ。在此过程中，每个动 作 θij(τ)被选择以最大化其奖励fj(θij(τ))。由于可能存在多 个源节点，在每个时隙 τ会选出一系列动作 θij(τ)、 vi、 vj ∈ V和 i ≠ j，并构成一个动作集合 Sτ。该时隙所有动作 获得的总奖励记为f(Sτ)，其中 f(Sτ) =∑θij(τ)∈Sτ fj(θij(τ))。 此外，在周期T内选择了一系列动作集合 Sτ、 τ ∈T。该系 列动作集合在周期T内获得的总奖励为∑τ∈T f(Sτ) =∑τ∈T ∑θij(τ)∈Sτ fj(θij(τ))。

当执行动作 θij(τ)时，相应的会消耗一些能量 cij 。 该时段内所有动作的总成本为∑τ∈T ∑θij(τ)∈Sτ cij。因此， 最优MESS实际上是寻找一系列动作集合，以最大化总奖励 fV(T)，如公式(1)所示，同时其每个时段的总成本受到限 制。 本文将能量共享问题表述为一个凸优化问题，其目 标是最大化网络总奖励，如下所示：

$$
\max \sum_{\tau \in T} \sum_{\theta_{ij}(\tau) \in S_\tau} f_j(\theta_{ij}(\tau)) \tag{1}
$$

$$
\text{s.t. } 0 < f_j(\theta_{ij}) < f_j(E_t^i(\tau - 1)), \forall v_i \in X_\tau, v_j \in R_\tau, \forall \tau \tag{2}
$$

$$
E_m^i(\tau) = E_m^i(\tau - 1) + E_h^i(\tau - 1) + E_r^i(\tau - 1) - E_t^i(\tau - 1) - E_c^i(\tau - 1), \forall v_i, \forall \tau \tag{3}
$$

$$
E_m^i(\tau) \leq E_m^{\max}, \forall v_i, \forall \tau.
$$

公式(2)中的第一个不等式成立，是因为接收器 v j接收 到的能量小于其发射器传输的能量，并且每个动作必须 获得正奖励。公式(3)是每个节点的能量更新函数。在公 式(3)中，当节点 vi为发射器时为 Er i(τ) = 0，当节点 vi 为接收器时为 Et i(τ) = 0。每个发射器由于能量共享必 须消耗自身能量 Et i − E r j，其中 vi是发射器， v j 是其 接收器。 Ec i 是 vi由于除能量共享外其他因素导致的能 量消耗。遗憾的是，找到最优方案是NP难的，其难度 证明类似于Tang等人（无日期）中定理3.1的证明。本 节对多跳能量共享问题进行建模，并给出寻找其可行解 的方法。

3.2 可行的多跳能量共享方案

问题(1)的解决方案实际上是找到源节点及其目标节点， 以及它们之间的能量共享路径，以最大化总奖励。然而， 能量传输与数据传输不同，因为前者要求能量必须从具 有较高能量水平的节点传输到能量水平较低的节点 层级。本文无法直接应用以往关于数据传输的宝贵方法。 本节给出了我们针对问题(1)的解决方案概要。为该问题 寻找最优解具有相当大的挑战性。本节提供了一种寻找 可行解的方法。我们首先通过以下定义明确什么是可行 解。

定义3.1 ： 如果一条多跳能量共享路径不存在必须阻断 该多跳能量共享的中继节点，并且其获得的总奖励为正， 则该多跳能量共享路径是可行的。

在整个网络中，可能存在多个同时进行的多跳能量共享 路径。多个源节点可以并行地向它们的源节点传输能量， 因此每次可能会有多个动作被执行。图3中的示例展示 了多跳能量共享过程的工作方式，并阐明了哪些类型的 多跳能量共享路径是可行的。在此示例中，引入了另一 个概念“轮次”。实际上，一轮是指在时隙 τ执行的动 作集合。这些动作可能针对不同的路径。存在两条路径， 分别是从 v1到 v4和从 vk到 vj。节点 v2和 v3在节点 v1 执行三个动作：θ12、 θ23和 θ34以将其能量传输给节点 v4 时起到中继能量的作用。从 v1到 v4的能量共享过程包 含多个轮次。我们在图3中展示了这些轮次。图中有以 下三轮。

第一轮包含两个动作： θ34和 θkj。 θ34将一“箱”能量 “a”从 v3传输到 v4。 θkj将一“箱”能量“d”从 vk传输 到 vj。 第二轮包含一个动作 θ23，该动作将一“箱”能量 “b”从 v2转移到 v3。 第三轮包含一个动作 θ12，该动作将一“箱”能量“c”从 v1转移到 v2。

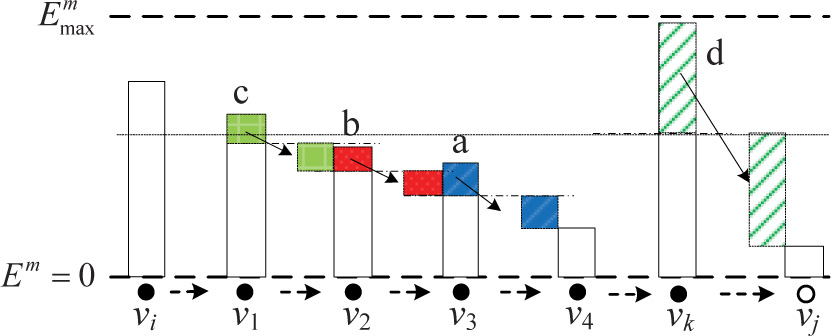
请注意，并非所有的多跳能量共享路径都是可行的。例 如，假设存在一条从 v4到 vj 的多跳能量共享，其中 vk 是如图3所示的中继节点。由于 vk 的剩余能量高于 v4 ， 即使 vk 首先向 vj 传输了一箱能量‘d’， v4 也无法向 vj 传输任何能量。在此，我们必须特别注意一种情况。例 如，存在另一条多跳能量共享： vi → vk → vj ，并假设 Em i = 3.5、 Em k = 5和Em j = 1。尽管从 vi 到 vj 的能量 共享路径由于 Em k > Em i 似乎不可行，但实际上它是可 行的，因为 vk 可以首先向 vj 传输两个单位的能量。从 根据该示例的提示，我们可以总结出寻找可行多跳能量 共享的方法。当每条链路上的能量消耗，即 c，不被考 虑时，可以通过给出以下引理来明确寻找可行能量共享 路径的方法。

引理1 ： 假设从 vi到 vj的多跳能量共享具有 h个中继节点， 且每条链路无成本，分别为vl、 l= 1，2，…， h。对于任意中 继节点 vq，若满足以下条件，则该多跳能量共享是可行的：

$$
\frac{1}{l+1} \left( \sum_{q=0}^{l} E_m^q + E_m^i \right) > \frac{1}{h-l+1} \left( \sum_{q=l+1}^{h} E_m^q + E_m^j \right) \tag{4}
$$

对于任意 l。

证明 1 ： 请参见附录7。

根据引理1，图3中的多跳能量共享 vk→vj和 vi→ v1 · · · → v4是可行的，而 v4→ vk→ vj不可行。

此外，当考虑每条链路上的能量消耗时，可行的能量共 享路径的条件由以下引理给出。

引理 2 ： 假设从v0到 vh+1的多跳能量共享具有 h 个中继节点，分别为 vl、 l= 1、2、......、 h。每条链路 （vk， vk+1）消耗的能量为 ck,k+1。对于任意中继节点 vq， 若满足以下条件，则该多跳能量共享路径是可行的：

$$
\frac{1}{l+1} \left( \sum_{q=0}^{l} E_m^q + E_m^0 - \sum_{k=0}^{l} c_{k,k+1} \right) > \frac{1}{h-l+1} \left( \sum_{q=l+1}^{h} E_m^q + E_m^{h+1} \right) \tag{5}
$$

对于任意 l。

证明 2 ： 请参见附录7。

3.3 分布式动作选择

找到可行的多跳能量共享作为问题(1)的可行解是一个直 接的选择。由于每个源节点的奖励函数是凸的，且效用 函数的总和仍然是凸的，因此上述问题是一个凸优化问 题。容易发现公式(1)中的约束是线性的。该问题可以通 过使用凸规划技术（如内点法(IPM)）以集中式方法求 解（Boyd and Vandenberghe, 2004）。因此，可以 在这种集中式方法下找到可行的多跳能量共享路径。然 而，在动态情况下，由于每个节点的剩余能量在能量共 享过程中是可变的（因为它可以获取能量或可能受到能 量耗散的影响），通过IPM求解该问题较为困难。

这种动态性使得寻找多跳能量共享的可行路径变得复杂 且困难。假设存在一条从 vi到 vj的多跳能量共享路径， 且 vk是它们之间的中继节点。但在该路径建立后， vk 从其他节点接收了一些能量，导致公式(4)无法满足。此 时，这条多跳能量共享路径将变为不可行的。实际上， 当考虑剩余能量的动态变化时，情况可能更加复杂。因 此，直接寻找多跳能量共享路径非常复杂且代价高昂。

本文改变了求解问题(1)的视角，并给出了不同于上 述直接方法的解决方案。首先，注意到根据引理4，若 多跳能量共享是可行的，则其中的每个动作都是可行的。 因此，我们得到以下推论：

推论3 ： 假设有 一组动作。如果该集合中的每个动作都是 可行的，则由该集合中的一些动作组成的多跳能量共享路径也 是可行的。

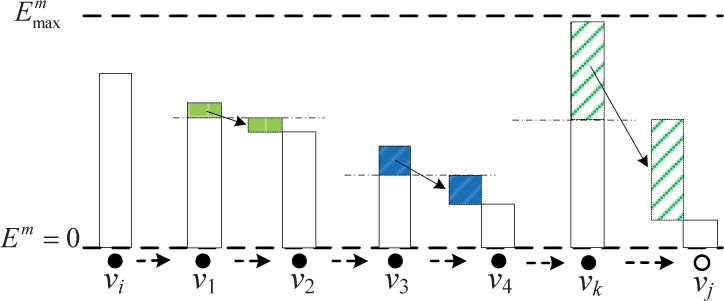
根据推论3，我们针对问题(1)的方案是寻找可行的同时 动作，而不是在整个网络中寻找多跳能量共享路径。例 如，图3实例中的多跳能量共享在图4中相应地转化为动 作选择。在该图中，动作是同时被选择的，且不一定属 于同一条多跳能量共享路径。由于上述问题的难度，下 一节将为此设计一个近似解决方案。

4 MESS的设计与分析

本节设计并分析了用于多跳能量共享的方案MESS。在 MESS中，我们针对两种情况分别提出了两种算法：静 态能量共享和动态能量共享。在第一种情况下，能量共 享是改变每个节点剩余能量的唯一因素，例如在夜间或 无阳光的日子，网络没有其他任务，因此除了共享的能 量外，没有能量被收集或消耗。在第二种情况下，除能 量共享外，还有其他因素会改变节点的剩余能量，例如 能量收集或由网络任务引起的能量耗散和消耗，因此每 个动作所获得的奖励可能存在误差。第二种情况比第一 种更贴近实际，但也更具挑战性。

4.1 静态能量共享

本模块提出了一种静态能量共享算法（SESA），该算法贪 婪地选择具有最高奖励的动作。理论上已证明，SESA能够 获得接近最优的奖励，同时其能量共享成本也是有界的。

在此情况下，每个节点仅在能量共享上消耗能量，因此公 式(3)中的项Eh i(τ − 1)和 Ec i(τ − 1)或它们的总和等于零。 公式(3)可重写如下：

$$
E_m^i(\tau) = E_m^i(\tau - 1) + E_r^i(\tau - 1) - E_t^i(\tau - 1), \quad \forall i, \forall \tau.
\tag{6}
$$

根据上述公式，SESA必须找到满足两个条件的接收器， 以最大化动作 θij的奖励。首先，SESA应在其邻域中寻 找剩余能量 Em i(τ − 1)最小的节点，因为这些节点对能 量的需求更迫切，即根据图2中的奖励函数，它们的斜 率高于其他节点。其次，这些节点应尽可能多地接收能 量，即最大化公式(6)中的项 Er j(τ − 1)。SESA如算法1 所示。SESA的核心思想是在每个时隙 τ同时选择其邻域 中剩余能量最小的节点，并将这些节点标记为接收器， 从而在 τ形成接收器集合 Rτ（见算法1的第3–6行）。 在节点集合 V中， Rτ的补集构成发射器集合 Xτ（见算 法1第7行）。之后，Rτ中的每个接收器在其 Xτ中寻找 对应的发射器，这些节点对构成动作集合 Gτ。根据能量 充电的特性，一个节点不能同时作为发射器和接收器， 且每个发射器/接收器在每个时隙只能对应一个接收器/ 发射器。通过SESA，每个接收器都能找到一个发射器， 从而形成一个动作，并且必须产生正向奖励。该动作选 择过程逐时隙重复进行，直到无法再选择新的动作为止。

参见图4所示示例。具有最小剩余能量的节点v j在时隙 τ 首先被选为接收器。由于 v4不在 v j的最大范围内， v4 也在同一时隙被选为接收器。类似地， v2和 vi在同一 时隙被选为发射器。随后， v j、 v4和 v2分别选择 vk、 v3和 v1作为其发射器，因此在 τ选出了三个动作。此 后，SESA进入下一轮，即 τ+= 1。

接下来，我们从理论上分析MESS的性质。根据算法 1，在 τ处选择了一些接收器 v i ∈ Rτ，它们中的每一个都 有其自身的奖励函数 fi。用 $ f_{R_\tau} = \sum_{v_i \in R_\tau} f_i $ 表示这些节点 的奖励总和。令 k τ表示在 τ处选择的接收器数量，即 $ k_\tau = |R_\tau| $，并用 θ l (τ)表示在该时隙选择的 l th动作，其中 $ 0 < l \leq k_\tau $ 且 $ \theta_l(\tau) \in S_\tau $。因此，当前 l th个动作被选择至 τ 时，动作集合为 $ S_{\tau}^l = {\theta_1, \theta_2, …, \theta_l} $。根据算法1，动作是 逐个选择的。根据图2所示的奖励函数性质，剩余能量较低 的节点具有更大的斜率。因此，以下方程成立。

$$
\theta_l(\tau) = \arg\max_{\theta_l(\tau) \in X_\tau \times R_\tau} \left{ \frac{f(S_{\tau}^{l-1} \cup {\theta_l(\tau)}) - f(S_{\tau}^{l-1})}{\Delta E(\theta_l(\tau))} \right}, \tag{7}
$$

其中， $\Delta E(\theta_l(\tau))$ 表示通过动作 $\theta_l(\tau)$ 所获得的接收能 量，而 $\theta_l(\tau)$ 是通过算法1的步骤9得到的。公式(7) 表示 算法1总是选择能够实现单位能量最大奖励的动作。于 是我们可以得到以下引理：

引理4 ： 对于任意的动作集合 S，其总奖励受以下不等式 限制。

$$
f(S) \leq f(S_\tau) + \Delta E(S) \cdot \frac{f(S_\tau \cup {\theta_m(\tau)}) - f(S_\tau)}{\Delta E(\theta_m(\tau))}, \tag{8}
$$

其中 θm表示在 S中能够实现单位能量最大奖励的动作。

算法1 静态能量共享算法（SESA）。
输入：节点集合 V 以及每个节点 vi的奖励函数 fi；
输出：周期T内的一系列动作GT。
1: 对每一轮 τ ∈T执行
2: 令 Xτ= V且 Rτ= ∅；
3: 当 Xτ ≠ ∅时执行循环
4: 在 Xτ中选择剩余 能量最小的节点 vj，并将其加入 Rτ；
5: Xτ= Xτ/Nj， 其中 vj ∈ Nj；
6: 结束循环
7: Xτ= V/Rτ；
8: 并行地对每个节点 vj ∈ Rτ执行
9: vj在 Xτ ∩Nj中选择一个 接收器 vi，使得 vi=arg max $ {E_i(\tau) - E_j(\tau) - c_{ij}} $，即选择一个动作 θij(τ)；
10: vi向 vj传输 $ \frac{E_m^i(\tau-1) - E_m^j(\tau-1) - c_{ij}}{2} $ 能量；
11: 将动作 θij(τ)添加到集合 Sτ中；
12: 从 Rτ中删除 vj；
13: 结束循环
14: Gτ= Gτ ∪{Sτ}；
15: τ+= 1；
16: 结束循环
17: 输出动作序列 GT。

Proof3 : 请参见附录7。

注意到上述引理中的集合 S是任意的，可假设其由问题 (1)的最优解得到。尽管无法直接获得最优解，但引理4 提示我们，算法1所获得的奖励可以非常接近最优解， 这一点由以下定理确定。

定理5 : 算法1获得的网络总奖励可以实现问题(1)的 $ 1 - \frac{1}{e} $ 近似。

证明4 ：设 G∗表示问题(1)的最优方案以及由最优能量共享 方案得到的动作集合。该最优解获得的最大奖励记为 f(G∗)。 注意到一个周期由若干时隙组成，且在每个时隙中，最优 方案选择 τ ∗ k个节点。令 $ K = \sum_{\tau \in T} k_\tau $。因此我们有子集 $ G^ = \bigcup_{\tau \in T} S_\tau^ $，其中 $ S_\tau^ $ 是在 τ时最优方案所选择的动作 集合。令 $ \Delta_\tau^l = f(S_\tau^ ) - f(S_\tau^l) $。于是根据引理4，有
$$
f(S_\tau^ ) \leq f(S_\tau) + \Delta E(S_\tau^ ) \cdot \frac{f(S_\tau \cup {\theta_m(\tau)}) - f(S_\tau)}{\Delta E(\theta_m(\tau))},
$$
其中 θm(τ)是能够在 Sτ中实现单位能量最大奖励的动作，即
$$
\Delta_\tau^l \leq \Delta E(S_\tau^ ) \cdot \frac{\Delta_\tau^l - \Delta_\tau^{l+1}}{\Delta E(\theta_m(\tau))}.
$$
对该不等式进行变换，可得
$$
\Delta_\tau^{l+1} \leq \Delta_\tau^l \left(1 - \frac{\Delta E(\theta_m(\tau))}{\Delta E(S_\tau^ )}\right).
$$
展开此不等式，可得
$$
\Delta_\tau^{k_\tau} \leq \Delta_\tau^1 \prod_{l=1}^{k_\tau} \left(1 - \frac{\Delta E(\theta_m(\tau))}{\Delta E(S_\tau^ )}\right).
$$
注意到 $\Delta E(\theta_m(\tau))$ 是 $S_\tau^ $ 中取得最大值的动作，因此其值必须大于 该集合中所有元素的平均值，即
$$
\Delta E(\theta_m(\tau)) \geq \frac{1}{k_\tau} \Delta E(S_\tau^ ).
$$
我们可以得到
$$
\Delta_\tau^{k_\tau} \leq \Delta_\tau^1 \prod_{l=1}^{k_\tau} \left(1 - \frac{1}{k_\tau}\right)^{k_\tau} < \Delta_\tau^1 \cdot \frac{1}{e} < f(S_\tau^ ) \cdot \frac{1}{e},
$$
因为 $\Delta_\tau^1 = f(S_\tau^ ) - f(S_\tau^1) < f(S_\tau^ )$。由于 $\Delta_\tau^{k_\tau} = f(S_\tau^ ) - f(S_\tau)$，有
$$
f(S_\tau) > \left(1 - \frac{1}{e}\right) f(S_\tau^ ).
$$
逐个时隙展开此不等式，我们得到
$$
\sum_{\tau \in T} f(S_\tau) > \sum_{\tau \in T} \left(1 - \frac{1}{e}\right) f(S_\tau^ ),
$$
即
$$
f(G_T) > \left(1 - \frac{1}{e}\right) f(G_T^ ).
$$
证明完毕。

本文的另一个目标是通过算法1对能量共享的总体成本进行 界定。设 G表示我们的方案以及由该方案获得的动作集合。 设 $c(G^ )$ 表示由 $G^ $ 产生的能量消耗， $c(G)$ 表示由MESS产生 的能量消耗。假设存在另一个方案 $G’$，该方案总是通过为 每个接收器寻找最近邻来执行每个动作。这些由 $G’$ 执行的 动作构成一个方案集合 $G’$。 $c(G’)$、 $c(G^ )$ 和 $c(G)$ 分别是 $G’$、 $G^ $ 和 $G$ 中所有动作的能量消耗总和。显然，必然有 $c(G’) \leq c(G^*)$。设 $X’$ 表示由 $G’$ 得到的源节点集合。我们可以得 到以下引理，用于界定我们方案的最大能量成本。

定理6 ： MESS方案的最大能量成本由最优解以
$$
c(G) \leq (n - 1) \max{c(G^*), E_m^{\max}}
$$
界定。

证明 5 ： 参见附录7。

4.2 动态能量共享

能量共享中的实际场景是每个节点的剩余能量可能是可 变的，这由以下几个原因造成。第一，每个节点都配备 了能量收集装置（如太阳能板），能够收集自然能源。 第二，节点可能承担除能量共享外的其他任务，例如通 信。第三，能量共享导致的能量耗散。我们将上述原因 引起能量变化合并为一项 δE i( τ)在 τ处，并基于公式 (3)和(6)得到以下方程。

$$
\delta E_i(\tau) = E_h^i(\tau - 1) - E_c^i(\tau - 1), \quad \forall v_i, \forall \tau. \tag{9}
$$

由于每个节点的电池容量有限，且根据第6节的调查和 第2节中的假设，上述能量变化相对较小，因此必须有
$$
-E_m^i(\tau - 1) < \delta E_i(\tau) \leq E_m^{\max} \quad \text{且} \quad \frac{\delta E_i(\tau)}{E_m^{\max}} \ll 1.
$$
一个非常实际的问题是能量变化如何影响网络的总奖励。 我们进行了理论分析，并将结论总结为定理7。

当每个发射器或接收器存在能量变化时，每个动作 θij(τ)所获得的奖励相应地具有误差ϵij(τ)，即 $f(\theta_{ij}(\tau)) + \epsilon_{ij}(\tau)$。$\epsilon_{ij}(\tau)$ 的真实值是动态的，由 $\delta E_i(\tau)$ 决定，并 包含来自发射器和接收器的两部分能量变化。但由于各 节点能量变化的分布高度依赖于具体应用，因此很难对 其分布进行建模。在本节中，我们的解决方案无需知晓 能量变化的分布情况。本节提供了一种简单的方法来分 析能量变化对网络奖励的影响。假设在时隙 τ开始时， 目标节点 vj找到其源节点vi后，完成能量共享需要时间 δτ，即选择了一个动作 θij(τ)。在 δτ期间，源节点和 目标节点可能分别产生能量变化 δEi(τ)或 δEj(τ)。容易 发现，当 δEi(τ) > 0或 δEj(τ) <0时，该动作 θij(τ)相比 时隙 τ开始时预期的奖励能带来更多的奖励；否则，该 动作带来的奖励会更少。在当前时隙 τ开始时，无法获 知 vi和 vj的能量变化。在我们的解决方案中，使用前 一时隙 τ − 1的能量变化来估计 τ时的能量变化，其中 每个发射器或接收器具有能量变化的概率为
$$
p_i(\tau - 1) = \frac{E_m^{\max} + \delta E_i(\tau - 1)}{2E_m^{\max}} \quad \text{或} \quad p_j(\tau - 1) = \frac{E_m^{\max} + \delta E_j(\tau - 1)}{2E_m^{\max}}.
$$
令 $p_{ij}(\tau - 1) = p_i(\tau - 1)p_j(\tau - 1)$。当发射器或接 收器的能量变化越大时，该动作实现更高奖励的概率也 越高。注意每个接收器必须对应一个发射器，因此对于 每个接收器 vi有 $\sum_{v_i \in \tilde{X} \tau \cap N_j / \tilde{R} \tau} p_{ij}(\tau - 1) = 1$。为了在 动态能量共享情况下选择若干动作以最大化总奖励，本 节设计了一种算法，称为DESA，如算法2所示，适用于 能量共享过程中每个动作所贡献的奖励呈动态变化的情 形。

根据算法2，当存在能量变化时，网络的总奖励在 最坏情况下被限制在$\tilde{f}$。通过算法2中的方案$\tilde{G} T$，在每个 时隙$\tilde{\tau}$都会选择一些动作，并记为 $\theta(\tau)$。动作 $\delta\theta {ij}(\tau)$ 的 能量变化记为 $\delta\theta_{ij}(\tau) = \delta E_i(\tau) - \delta E_j(\tau)$，其中能量从 $v_i$ 转移到 $v_j$。该动作由于其能量变化所引起的奖励变 化为 $f(\delta\theta_{ij}(\tau))$。为方便起见，我们将 $\theta_{ij}(\tau)$ 记作 $\theta_l(\tau)$， 表示 $\theta_l(\tau)$ 是在 τ选择的动作。因此，算法2实际上以一 定概率选择在存在能量变化时能够实现最大奖励的每个 动作，即动作 $\theta_l(\tau)$ 满足以下方程：

$$
\theta_l(\tau) = \arg\max_{\theta_l(\tau) \in X_\tau \times R_\tau} \left{ \frac{f(S_{\tau}^{l-1} \cup {\theta_l(\tau)}) - f(S_{\tau}^{l-1})}{\Delta E(\theta_l(\tau))} + p_l(\tau - 1)f(\delta\theta_l(\tau)) \right}.
$$

上述方程表明了一个事实：当前时隙的能量变化在该时 隙开始时无法获知，只能通过前一时隙的值进行估计， 但奖励误差的实际值可以在之后被精确计算。这属于利 用或探索问题，但我们理论上可以捕捉到奖励误差。在 算法2中，选择概率最高的动作，而每个动作可能会对 其奖励产生误差。用 $\epsilon_l(\tau)$ 表示该动作产生的奖励误差， 即 $\epsilon_l(\tau) = f(\delta\theta_l(\tau))$。关于算法2所选择的所有动作的奖 励误差，本节有如下定理。

算法 2 动态能量共享 算法 (DESA)
输入：节点集合 V 和奖励函数 fi，用于 每个节点 vi。
输出：能量共享方案 $\tilde{G} T$ 对所有源节点 $v_i \in \tilde{X}_T$ 在周期T内；
1: 对每一轮 τ ∈T执行
2: Let $\tilde{X} \tau = V$ 和 $\tilde{R} \tau = \emptyset$；
3: 当 $\tilde{X} \tau \neq \emptyset$ 执行
4: 选择一个剩余能量最小的节点 vj in $\tilde{X} \tau$，并将它们加入 $\tilde{R} \tau$;
5: $\tilde{X} \tau = \tilde{X} \tau / N_j$，其中 vj ∈ Nj；
6: 结束当循环
7: $\tilde{X} \tau = V / \tilde{R} \tau$;
8: 对于每个节点 vj ∈ $\tilde{R} \tau$ 并行执行
9: vj计算 the概率 $p {ij}(\tau - 1)$， and选择 a接收器 vi with最高 概率 $p_{ij}(\tau)$, in $\tilde{X} \tau \cap N_j$ such that
$ v_i = \arg\max {v_i \in X_\tau} {E_i(\tau) - E_j(\tau) - c_{ij}} $, 即, an ˜动作 $\theta_{ij}(\tau)$ 被选择；
10: vi传输 $ \frac{E_m^i(\tau-1) - E_m^j(\tau-1) - c_{ij}}{2} $ 能量到 vj；
11: 添加动作 $\tilde{\theta} {ij}(\tau)$ 到集合中 $\tilde{S} \tau$;
12: 从 vj 删除 $\tilde{R} \tau$;
13: 结束循环
14: $\tilde{G} \tau = \tilde{G} \tau \cup {\tilde{S} \tau}$;
15: τ += 1;
16: 结束循环
17: 输出能量共享方案 $\tilde{G}_T$.

定理7 ：当能量共享过程中存在能量变化时，算法2获得 的总奖励以高概率不低于 $(1 - \frac{1}{e})f(G^ ) + \sum_{\tau \in T} E(\Delta_\tau)$，其中 $G^ $ 是最优方案的动作集合， $E(\Delta_\tau) = \sum_{l=1}^{k_\tau} \Delta_\tau^l$ 且 $\Delta_\tau^l = f(S_\tau^*) - f(\tilde{S}_\tau^l)$。

Proof6 : 根据引理4，我们可以很容易地得到以下方程：
$$
f(S) \leq f(\tilde{S} \tau) + \Delta E(S) \cdot \frac{f(\tilde{S} \tau \cup {\tilde{\theta} m(\tau)}) - f(\tilde{S} \tau)}{\Delta E(\tilde{\theta} m(\tau))}. \tag{10}
$$
设 $G^ $ 为问题(1)的最优方案，该最优解获得的最大奖励 记为 $f(G^ )$，其中 $G^ $ 是由最优解确定的最优能量共享调度集合。该定理 的证明与定理5的证明非常相似。令 $\Delta_\tau^l = f(S_\tau^ ) - f(\tilde{S} \tau^l)$。 因此根据公式(10)，有
$$
f(S_\tau^ ) \leq f(\tilde{S} \tau) + \Delta E(S \tau^ ) \cdot \frac{f(\tilde{S} \tau \cup {\tilde{\theta}_m(\tau)}) - f(\tilde{S} \tau)}{\Delta E(\tilde{\theta} m(\tau))},
$$
其中 $\tilde{\theta}_m(\tau)$ 是在 $\tilde{S} \tau$ 中能够实现单位能量最大奖励的动作，即
$$
\Delta_\tau^l \leq \Delta E(S_\tau^ ) \cdot \frac{\Delta_\tau^l - \Delta_\tau^{l+1}}{\Delta E(\tilde{\theta} m(\tau))}.
$$
因此有
$$
\Delta \tau^{l+1} \leq \Delta_\tau^l \left(1 - \frac{\Delta E(\theta_m(\tau))}{\Delta E(S_\tau^ )}\right).
$$
回顾一下，在算法2中获得的每个 动作可能会以概率 $p_l(\tau - 1)$ 产生误差 $\epsilon_{\tilde{\theta} m(\tau)}$，因为 $\Delta E(\tilde{\theta}_m(\tau))$ 是在算法2的前一时隙 τ − 1估计得到的，即
$$
\Delta E(\tilde{\theta}_m(\tau)) = \Delta E(\theta_m(\tau)) + p_m(\tau)\delta\theta_m(\tau).
$$
因此我们有
$$
\Delta \tau^{l+1} \leq \Delta_\tau^l \left(1 - \frac{\Delta E(\theta_m(\tau))}{\Delta E(S_\tau^ )} + \frac{p_m(\tau)\delta\theta_m(\tau)}{\Delta E(S_\tau^ )}\right) = \Delta_\tau^l \left(1 - \frac{\Delta E(\theta_m(\tau))}{\Delta E(S_\tau^ )}\right) + \Delta_\tau^l \cdot \frac{p_m(\tau)\delta\theta_m(\tau)}{\Delta E(S_\tau^ )}.
$$
令 $\sigma_{m,\tau} = \frac{p_m(\tau)\delta\theta_m(\tau)}{\Delta E(S_\tau^ )}$，于是我们得到以下不等式：
$$
\Delta_\tau^{l+1} \leq \Delta_\tau^l \left(1 - \frac{\Delta E(\theta_m(\tau))}{\Delta E(S_\tau^ )}\right) + \sigma_{m,\tau} \Delta_\tau^l. \tag{11}
$$
请注意，必须满足 $0 < \frac{\Delta E(\theta_m(\tau))}{\Delta E(S_\tau^ )} < 1$，因此有 $0 < 1 - \frac{\Delta E(\theta_m(\tau))}{\Delta E(S_\tau^ )} < 1$。于是展开不等式(11)，可得
$$
\tilde{\Delta} {k \tau} \leq \Delta_\tau^1 \prod_{l=1}^{k_\tau} \left(1 - \frac{\Delta E(\theta_m(\tau))}{\Delta E(S_\tau^ )}\right) + \sum_{l=1}^{k_\tau} \sigma_{l,\tau} \Delta_\tau^l. \tag{12}
$$
类似于定理5的证明，我们可以得到
$$
f(\tilde{S} \tau) > \left(1 - \frac{1}{e}\right) f(S \tau^ ) - \sum_{l=1}^{k_\tau} \sigma_{l,\tau} \Delta_\tau^l.
$$
逐个时隙展开该不等式，我们有
$$
\sum_{\tau \in T} f(\tilde{S} \tau) > \sum {\tau \in T} \left(1 - \frac{1}{e}\right) f(S_\tau^ ) - \sum_{\tau \in T} \sum_{l=1}^{k_\tau} \sigma_{l,\tau} \Delta_\tau^l.
$$
$$
f(\tilde{G}_T) > \left(1 - \frac{1}{e}\right) f(G_T^ ) - \sum_{\tau \in T} E(\Delta_\tau),
$$
其中 $E(\Delta_\tau) = \sum_{l=1}^{k_\tau} \sigma_{l,\tau} \Delta_\tau^l$。证明完毕。

接下来，本节考虑上述定理的一个特例，其中误差在每 个动作上均匀且随机地发生。因此，根据定理7，奖励 误差由以下引理给出。

定理8 ： 当能量共享期间存在能量变化，且每次动 作时能量变化均匀且随机发生时，算法2获得的总奖励 满足以下不等式：
$$
f(\tilde{G} \tau) > \left(1 - \frac{2}{e}\right) f(G \tau^ ) \tag{13}
$$
该定理的证明相当直接。注意定理7中的误差项 $\sum_{l=1}^{k_\tau} \sigma_{l,\tau} \Delta_\tau^l$。
$$
\sum_{l=1}^{k_\tau} \sigma_{l,\tau} \Delta_\tau^l = \sigma_\tau \sum_{l=1}^{k_\tau} \Delta_\tau^l \leq \sigma_\tau \Delta_\tau^1 \left[(1 - \frac{1}{2}) + (1 - \frac{1}{3})^2 + \cdots + (1 - \frac{1}{k_\tau})^{k_\tau - 1}\right] < \sigma_\tau \frac{k_\tau}{e} f(S_\tau^ ) < \frac{1}{e} f(S_\tau^*).
$$

5 评估

本文选择仿真作为主要研究工具，以了解系统在不同条件 下的行为规模。对MESS性能评估的仿真由Omnet++仿真工 具（http://www.omnetpp.org/）进行。在此仿真中， 每个节点被设置具有 1mAH（即3600 毫安秒）的初始 能量，且每个时隙可获取的能量为期望值15 毫安、方差 15 毫安的随机变量。节点被随机部署在一个大小为 500 × 500平方米的固定大小区域中。每个节点每分钟 采集数据并生成一个数据包。能量共享成本设为0.6( $ \frac{d}{d_{\max}} $ )²∆E，其中 $d_{\max}$ 是节点利用其全部初始能量能够 传输能量的最大距离。在我们的仿真中，MAC层和网络 层分别实现了IEEE 802.11协议（IEEE标准，1999年） 和最小跳数路由。因此，本文直接采用DESA算法，因 为协议和路由在能量共享过程中的通信消耗大量能量。

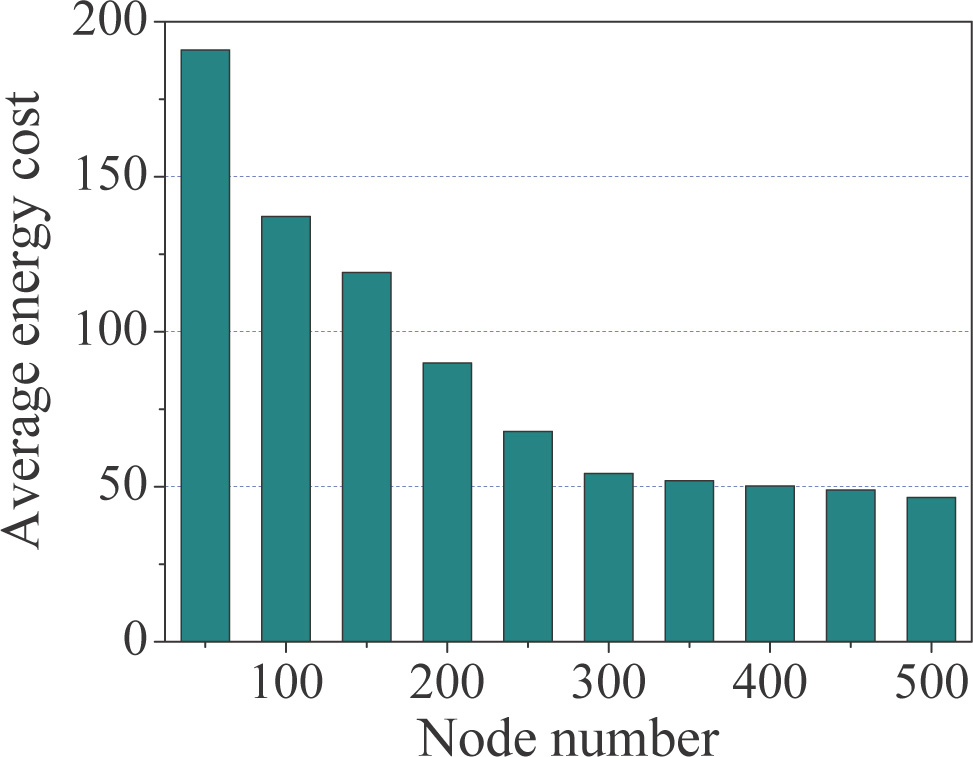
仿真结果如图5–8所示，比较了网络分别采用能量 共享算法DESA和无能量共享算法时的性能。图5显示， 采用能量共享算法DESA的网络平均剩余能量低于采用 无能量共享算法的情况。这是由于能量共享及其消息通 信带来的能量消耗所致，如图8所示。图8展现了在不同 节点数量下的平均能量消耗。

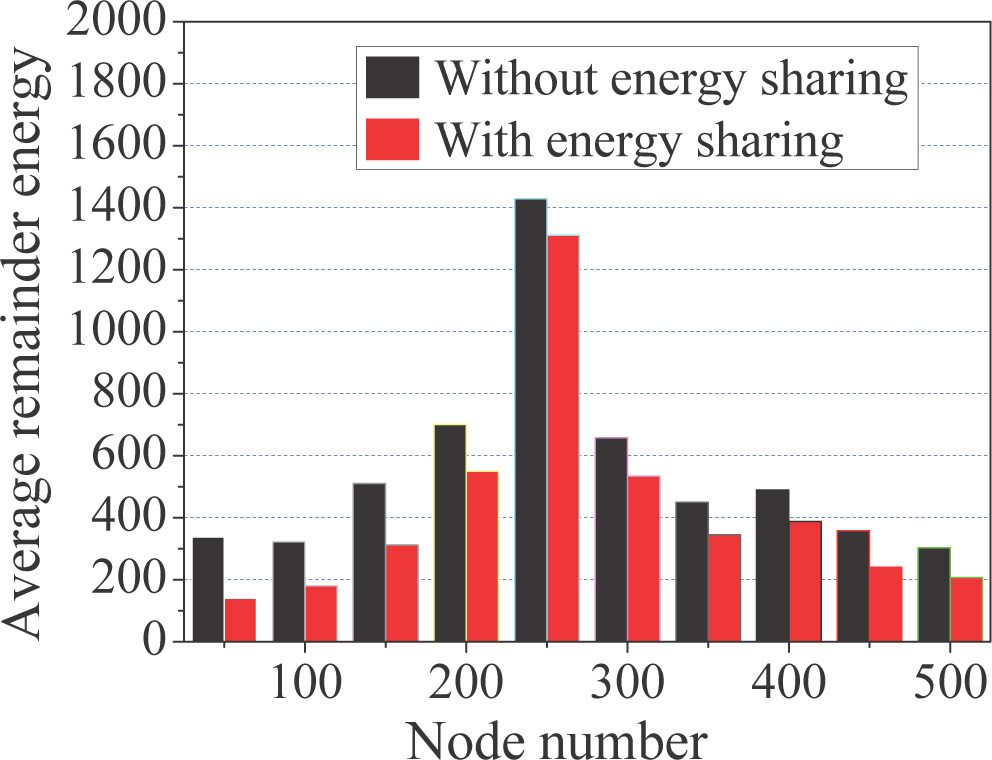
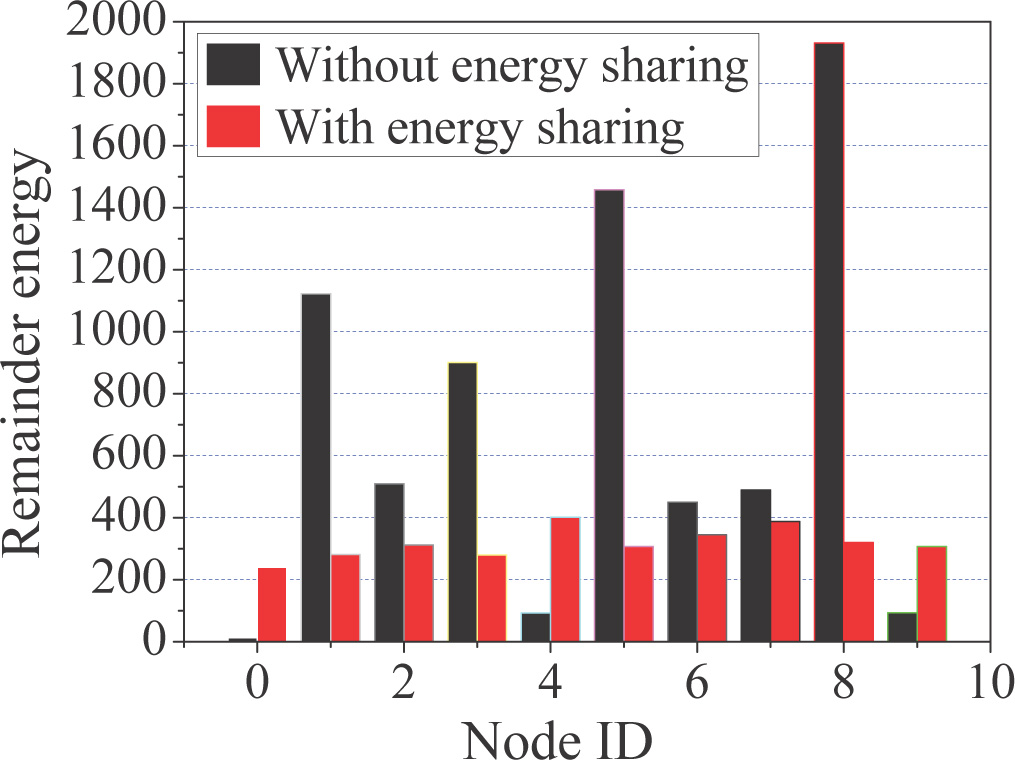
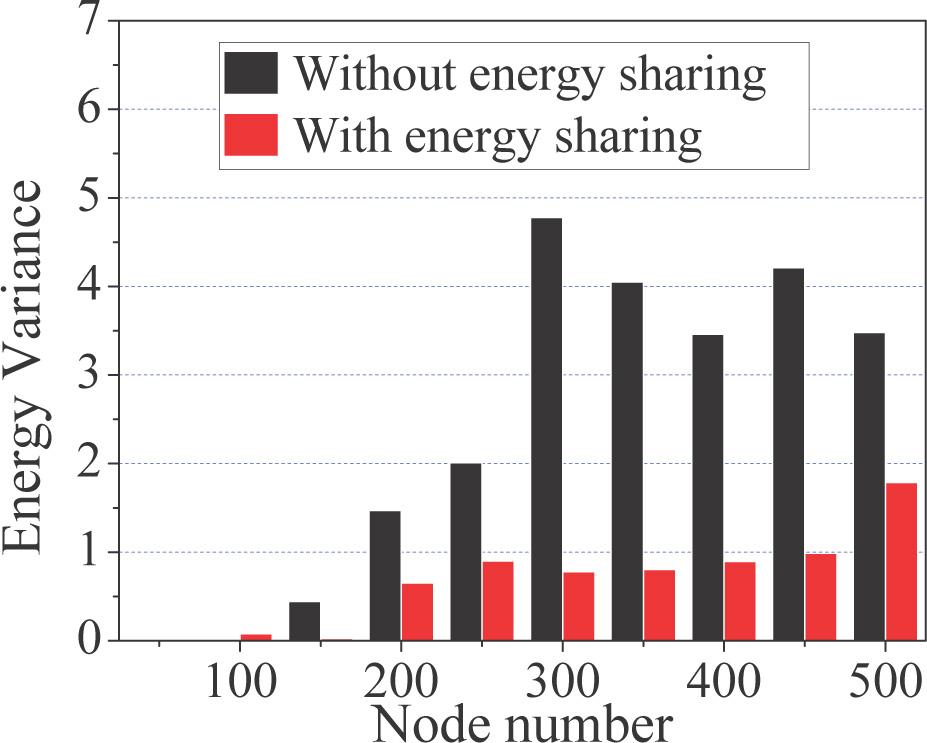
图5并不意味着在DESA下工作的网络的生命周期比没有 能量共享时更短。图7显示了剩余能量方差，该方差表 示各节点剩余能量与平均剩余能量之差的平均平方。我 们在仿真中选取了10个节点，仿真中共有150个节点。 这10个节点的编号范围为0到9。由于所有节点均为随机 部署，这10个节点是

还被随机选出。如图6所示，当分别采用MESS和无能量 共享算法时，这10个节点的剩余能量各不相同。当采用 无能量共享算法时，节点 v0、 v4和 v9的剩余能量分别 为22.89、92.832和63.447 毫安秒，远低于使用 MESS时的剩余能量。这些节点将首先死亡，导致网络 必须停止工作。同时，采用算法DESA时剩余能量最少 的节点是 v0，其剩余能量为240.29 毫安秒。

影响能量共享成本的主要因素是节点间距离。由于节点 部署在固定大小的区域内，当节点总数较少时，节点间 的平均距离更小，如图8所示。我们还发现，较高的节 点密度并不一定会导致能量共享期间的能量消耗降低。 例如，在图8中，当节点数量从300增加到500时，能量 消耗没有明显差异。当节点密度过高时，无线信道竞争 也随之加剧，部分能量共享消息丢失，导致一些动作无 法完成。这也是图7中当节点数量增加时能量方差增大 的原因。

6 相关工作

通过无线能量传输的能量共享已在一些领域得到广泛应用， 例如带有无源标签的射频识别系统（海因里希和皮莱， 2005；Tang 等，2009）。在尼古拉·特斯拉于20世纪初对 无线能量传输的研究基础上，Kurs 等人 (2007) 通过在强 耦合模式下使用自谐振线圈，实验验证了在距离达到线圈 半径8倍时仍能高效实现非辐射性功率传输。新近讨论的技 术：无线 充电促进了其在无线网络中的应用发展。近年来越来越 多的研究（Zhu 等，2010；Li 等，2010；Peng 等， 2010；Tong 等，2010；Shi 等，2011）聚焦于多跳传 感器网络中的能量共享，但并未涉及多跳能量共享。 Zhu 等（2010）首次将能量共享引入传感器网络，并在 能量路由器及其相关协议设计方面进行了有趣且可行的 尝试。Tong 等（2010）研究了无线充电技术对传感器 网络部署和路由安排的影响，并开发了启发式算法来解 决其形式化的部署与路由问题。还有其他研究主张使用 移动充电器为传感器节点充电（Peng 等，2010；Shi 等，2011；Li 等，2011），并尝试寻找移动充电车辆的 最优行驶路径。在现有传感器网络能量共享研究中，能 量通过移动充电器从基站传输到传感器节点。本文与以 往工作有显著不同，研究了多跳能量共享及其高性能方 案。

能量收集装置或平台，例如 Helimote（Hsu 等人， 2005）、Prometheus（Jiang 等人，2005）和 AmbiMax（Park 和 Chou，2006），曾被尝试用于实 现无线传感器网络的可持续运行。但这些方法可能加剧 节点间的能量不公平性，因为每个节点所能获取的能量 有限且具有随机性（Gu 等人，2009；He 等人，2011）。 环境能量（如太阳能、风能）通常不足以在长期运行中 支持传感器节点持续的全占空比工作（Kansal 等人， 2004；Jiang 等人，2005；Zhu 等人，2009）。Gu 等人（2009）进行了实验，其结果表明能量收集节点的占 空比仅能在 0.2% 到 9.78% 之间。Shen 等人（2013） 的实验显示，太阳能板每天获取的能量少于容量为 2200 mAH 的 AA型镍氢电池能量的 10%。尽管每日获 取的能量相对于电池容量而言非常小，但如果在 20 天 或更长时间内未被使用，这些能量将积累或被浪费。本 文考虑了能量收集与消耗等因素对能量共享过程中计算 等方面的影响，而此前的相关工作并未考虑这一点。

7 结论

本文提出了一种基于新近研究的能量共享技术的新型能 量共享方案：多跳能量共享。据我们所知，我们是首次 提出此类能量共享方案的研究者。与数据通信不同，寻 找可行的能量共享路径具有较大挑战性。我们给出了寻 找可行的多跳能量共享路径的条件。基于该条件，我们 设计了方案 MESS以找出最优的可行多跳能量共享路 径，从而最大化总奖励。在 MESS中，分别针对静态 和动态能量共享两种情况设计了SESA和DESA两种算法。 对于这两种算法， MESS的理论性能几乎达到了 $1 - \frac{1}{e}$ 最优解。我们的仿真经过精心设计和实现，实验结果表 明能量公平性可以得到显著提升。本文的方案是集式的， 我们将设计一个分布式方案作为未来工作。