所谓拓扑排序就是对一个有向无环图G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边<u,v>∈E(G),则u在线性序列中出现在v之前。
可能这个定义有点难理解,那接下来我就说说它的具体流程。(真的容易理解的)
进入正题
随便的给你一个有向无环图
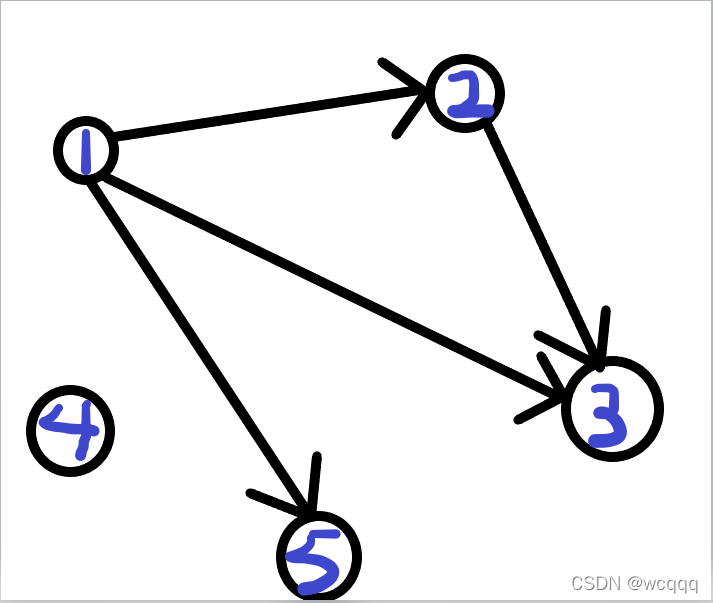
1:找到入度为0的点
就像此图,它入度为0的点是1和4,将它们取出来,记为第一个数和第二个数。并且把与它们有关的边都去掉(这个图就没有哈)
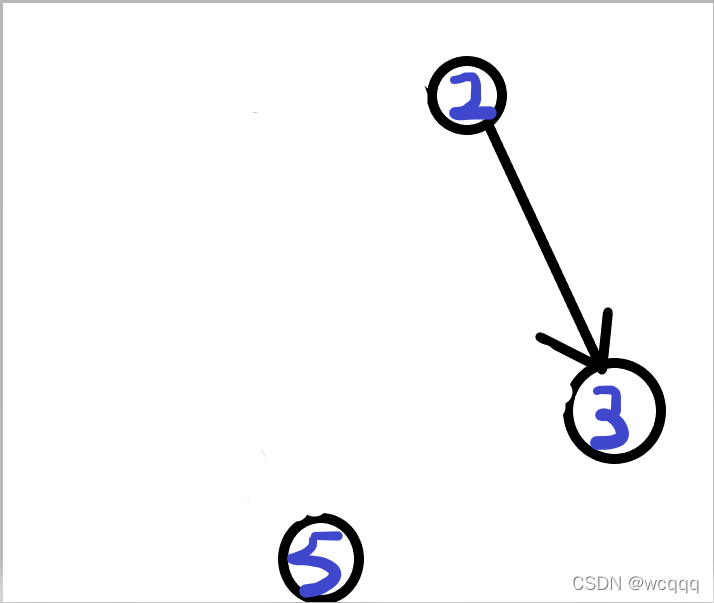
2:重复上述操作。
取出入度为0的点,现在入度为0的点是2,5,把它们记作第3个数和第4个数。把它们相邻的边去掉。

最后一个数就是3了。
根据取出的顺序进行排序,就是1,4,2,5,3.
所以拓扑排序是不是很容易呢?
接下来就给出拓扑排序的模板。
1:初始化模板。
for(int i=1; i<=m; ++i) {//m条边
cin>>x>>y;
edge[x].push_back(y);
in[y]++;//in[i]表示入度
}
for(int i=1; i<=n; ++i) {//n个点
if(in[i]==0) {
q.push(i);//入度为0就把它加入队列
}
}2:拓扑排序函数模板
void topology_sort() {
while(!q.empty()) {
int t=q.front();
ans.push_back(t);
q.pop();
for(int i=0; i<edge[t].size(); ++i) {
in[edge[t][i]]--;
if(in[edge[t][i]]==0) q.push(edge[t][i]);
}
}
}其实拓扑排序最大的好处是判断有无环。我们可以根据取出来点的数量和点的个数进行比较。
如果取出来点的数量和点的个数相同,那么它是无环的。如果取出来点的数量小于点的个数则是有环的。
来上模板题!!!
题目链接:拓扑排序模板题
题意:给你n个点,m条边,对它们拓扑排序。输出排序结果。
解析:没啥好说的,直接上模板代码。反正这题记得初始化清空就行了。
#include<bits/stdc++.h>
#include<queue>
#include<vector>
using namespace std;
int in[105];
queue<int>q;
vector<int>edge[105];
vector<int>ans;
void topology_sort() {
while(!q.empty()) {
int t=q.front();
ans.push_back(t);
q.pop();
for(int i=0; i<edge[t].size(); ++i) {
in[edge[t][i]]--;
if(in[edge[t][i]]==0) q.push(edge[t][i]);
}
}
}
int main( ) {
int n,m,x,y;
while(cin>>n>>m) {
ans.clear();
for(int i=1; i<=100; ++i) {
edge[i].clear();
}
memset(in,0,sizeof(in));
if(n==0&&m==0) return 0;
for(int i=1; i<=m; ++i) {//m条边
cin>>x>>y;
edge[x].push_back(y);
in[y]++;//in[i]表示入度
}
for(int i=1; i<=n; ++i) {//n个点
if(in[i]==0) {
q.push(i);//入度为0就把它加入队列
}
}
topology_sort();
for(int i=0; i<ans.size(); ++i) {
cout<<ans[i]<<" ";
}
cout<<endl;
}
return 0;
}来道例题
题目链接:稍难的拓扑排序
这是一道cf上面的题目,居然有1800分的难度。
C. Book
You are given a book with nn chapters.
Each chapter has a specified list of other chapters that need to be understood in order to understand this chapter. To understand a chapter, you must read it after you understand every chapter on its required list.
Currently you don't understand any of the chapters. You are going to read the book from the beginning till the end repeatedly until you understand the whole book. Note that if you read a chapter at a moment when you don't understand some of the required chapters, you don't understand this chapter.
Determine how many times you will read the book to understand every chapter, or determine that you will never understand every chapter no matter how many times you read the book.
Input
Each test contains multiple test cases. The first line contains the number of test cases t (1≤t≤2*1e4).
The first line of each test case contains a single integer n (1≤n≤2*1e5) — number of chapters.
Then nn lines follow. The ii-th line begins with an integer ki(0≤ki≤n−1) — number of chapters required to understand the ii-th chapter. Then kiki integers ai,1,ai,2,…,ai,ki(1≤ai,j≤n,ai,j≠i,ai,j≠ai,l,for j≠l) follow — the chapters required to understand the i-th chapter.
It is guaranteed that the sum of nn and sum of kiki over all testcases do not exceed 2*1e5.
Output
For each test case, if the entire book can be understood, print how many times you will read it, otherwise print −1.
题意:给你n本书,在读第i本书之前,你必须先读x本书。而且可以进行一系列的操作,每次操作是从第一本到第n本书,去阅读你目前可以读的书。求最少的操作数使得你能够阅读完所有书籍。
解析:此题可以变为一个有向图。就是一个拓扑排序的模板,但是唯一的不同是,它要记录每个点取出来时候的轮数。最后的答案就是轮数的最大值。而如果是个环就输出-1。这题有个细节就是我们要用优先队列来保证小的数先取出来。
#include<bits/stdc++.h>
#include<queue>
#include<vector>
using namespace std;
int in[200005];
pair<int,int> t;
int Max;
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > >q;
vector<int>edge[200005];
vector<int>ans;
void topology_sort() {
while(!q.empty()) {
Max=max(Max,q.top().first);
t=q.top();
ans.push_back(t.second);
q.pop();
for(int i=0; i<edge[t.second].size(); ++i) {
in[edge[t.second][i]]--;
if(in[edge[t.second][i]]==0) {
if(edge[t.second][i]>t.second) {
q.push(make_pair(t.first,edge[t.second][i]));
} else q.push(make_pair(t.first+1,edge[t.second][i]));
}
}
}
}
int main( ) {
int t,x,u,n;
cin>>t;
while(t--) {
ans.clear();
for(int i=1;i<=20000;++i){
edge[i].clear();
}
memset(in,0,sizeof(in));
Max=0;
cin>>n;
for(int i=1; i<=n; ++i) {
cin>>x;
for(int j=1; j<=x; ++j) {
cin>>u;
edge[u].push_back(i);
in[i]++;
}
}
for(int i=1; i<=n; ++i) {
if(in[i]==0) {
q.push(make_pair(1,i));
}
}
topology_sort();
if(ans.size()!=n) cout<<-1<<endl;
else cout<<Max<<endl;
}
return 0;
}拓扑排序(入门)就这样结束啦。难的拓扑排序还会跟tarjan算法结合,跟dp结合(TAT)。希望以后这些学完,再来讲讲。





 本文详细介绍了拓扑排序的基本概念,通过实例演示如何进行有向无环图的节点排列,并提供了两个模板题目的解决方案,包括判断有环和计数操作次数。深入浅出地讲解了拓扑排序在实际问题中的应用,如书籍阅读顺序和编程竞赛中的复杂逻辑理解。
本文详细介绍了拓扑排序的基本概念,通过实例演示如何进行有向无环图的节点排列,并提供了两个模板题目的解决方案,包括判断有环和计数操作次数。深入浅出地讲解了拓扑排序在实际问题中的应用,如书籍阅读顺序和编程竞赛中的复杂逻辑理解。
















 1060
1060

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








