Educational Codeforces Round 112 (Rated for Div. 2)（A~D）

比赛链接https://codeforces.com/contest/1555

A. PizzaForces

题意：给你一个数n，你有三种方式去把0增加到至少为n，但这三种方式所用的时间都不相同。求花费时间的最小值。

这三种方式为：1：增加6，时间花费10；

                          2：增加8，时间花费20；

                          3：增加10 ，时间花费25；

解析：首先不难发现一个规律，增加的时间均为增加数的2.5倍。只要所以这个数刚好能6，8，10组成的话，则答案就为2.5*n。所以又有一个规律，6，8，10刚好可以组成大于6的所有偶数。所以分个小于6和大于6的数是偶数还是奇数讨论一下就可以得出答案咯。、

#include<bits/stdc++.h>
using namespace std;
int main( ){
	int t;
	long long n;
	cin>>t;
	while(t--){
		cin>>n;
		if(n<=6) cout<<15<<endl;
		else{
			if(n%2==0) cout<<n/2*5<<endl;
			else cout<<(n+1)/2*5<<endl; 
		}
	}
	
	
} 

B. Two Tables
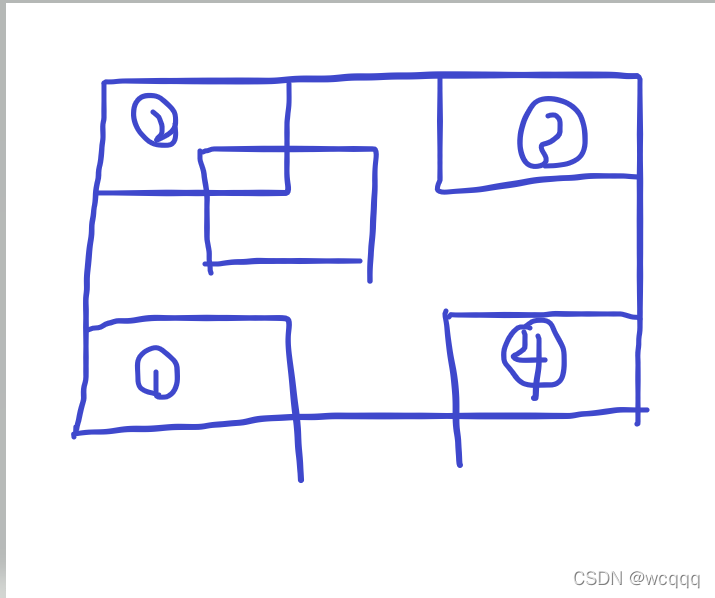
题意，给你一个大矩形，两个小矩形（第一输入的小矩形是可以移动的）。叫你求出在这个大矩形里面移动第一个小矩形的最小距离，使得两个小矩形不相交。

解析：贪心的思想，想要求距离最短，必然是直线距离。所以分第二块小矩形在大矩形四个角落，求出第一块矩形要移动多少距离，才能不相交就行了。最后取个最小值就是答案了。（如图所示）

 

#include<bits/stdc++.h>
using namespace std;
int main( ) {
	int w,h;
	int t,W,H,x1,x2,y1,y2;
	cin>>t;
	while(t--) {
		int Min=1e9;
		cin>>W>>H;
		cin>>x1>>y1>>x2>>y2;
		cin>>w>>h;
		if(x1<=w&&y1<=h) {
			if(w+x2-x1<=W)
				Min=min(Min,w-x1);
			if(h+y2-y1<=H)
				Min=min(Min,h-y1);
		} else Min=0;
		if(x1<=w&&y2>=H-h) {
			if(w+x2-x1<=W)
				Min=min(Min,w-x1);
			if(H-h-(y2-y1)>=0)
				Min=min(Min,y2-(H-h));
		} else Min=0;
		if(x2>=W-w&&y2>=H-h) {
			if(W-w-(x2-x1)>=0)
				Min=min(Min,x2-(W-w));
			if(H-h-(y2-y1)>=0)
				Min=min(Min,y2-(H-h));
		} else Min=0;
		if(x2>=W-w&&y1<=h) {
			if(W-w-(x2-x1)>=0)
				Min=min(Min,x2-(W-w));
			if(h+y2-y1<=H)
				Min=min(Min,h-y1);
		} else Min=0;
		if(Min==1e9) cout<<-1<<endl;
		else cout<<fixed<<setprecision(9)<<double(Min)<<endl;
	}
}

C. Coin Rows

题意：给你两行数，首先是小A先走，之后是小B走。他们只能往右或者往下走，而且小A走过的数都会变成0。而最终的成绩取决于小B走到的数字之和。小A希望最终成绩低，但小B希望成绩高。

 

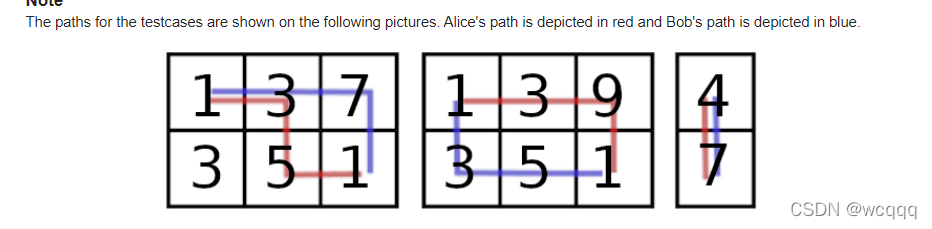
解析:这题暴力一遍就完事了。首先用个前缀和（第一行sum1,第二行sum2），求出每行的前i个数之和，之后把拐点的位置从1遍历到n，所以每次最终成绩就变为max(sum1[m]-sum1[i],sum2[i-1])求出小A希望最终成绩低的位置记为pos。最后答案就是max(sum1[m]-sum1[pos],sum2[pos-1])

（这题其实比B题简单很多）

#include<bits/stdc++.h>
using namespace std;
int a[100005],b[100005],sum1[100005],sum2[100005];
int main( ){
	int t,m;
	cin>>t;
	while(t--){
		memset(sum1,0,sizeof(sum1));
		memset(sum2,0,sizeof(sum2));
		cin>>m;		
		for(int i=1;i<=m;++i){
			cin>>a[i];
			sum1[i]=sum1[i-1]+a[i];
		}
		for(int i=1;i<=m;++i){
			cin>>b[i];
			sum2[i]=sum2[i-1]+b[i];
		}
		int Min=1e9+5;
		int pos=0;
		for(int i=1;i<=m;++i){
			if(Min>max(sum1[m]-sum1[i],sum2[i-1])){
				Min=max(sum1[m]-sum1[i],sum2[i-1]);
				pos=i;
			}
		}
		cout<<max(sum1[m]-sum1[pos],sum2[pos-1])<<endl; 
	}	
}  

D. Say No to Palindromes

题意：给你一个字符串，有m次询问，每次询问给你一个区间。叫你求出，使得这一区间的字符串变为漂亮字符串的最小操作数。漂亮字符串：没有字符串长度为2以及以上的回文串。操作：可以把任意的字母变为‘a’，‘b’，‘c’的任意一个。

解析：采用dp。其实若要变为漂亮的字符串就只有6种情况（abc，acb，bac，bca，cab，cba这六个字符串任意一个不断与自身连接）所以要把原来字符串变为这六种情况的所需的最小操作数(预处理操作）。询问时候输出最小值即可

#include<bits/stdc++.h>
using namespace std;
int f[15][200005];
char s[200005];
string ss[10]= {"0","abc","acb","bac","bca","cab","cba"};
int main( ) {
	int n,m,l,r;
	cin>>n>>m;
	cin>>s+1;
	int len=strlen(s+1);
	for(int i=1; i<=6; ++i) {
		for(int j=0; j<len; ++j) {
			if(s[j+1]==ss[i][(j+1)%3])
				f[i][j+1]=f[i][j];
			else f[i][j+1]=f[i][j]+1;
		}
	}
	while(m--) {
		cin>>l>>r;
		int Min=1e9;
		for(int i=1; i<=6; ++i) {
			Min=min(Min,f[i][r]-f[i][l-1]);
		}
		cout<<Min<<endl;
	}
}