Group Normalization

https://arxiv.org/pdf/1803.08494.pdf
https://github.com/facebookresearch/Detectron/blob/master/projects/GN
Weight-Normalization https://github.com/openai/pixel-cnn
Weight-Normalization https://github.com/zoli333/Weight-Normalization

---

Abstract

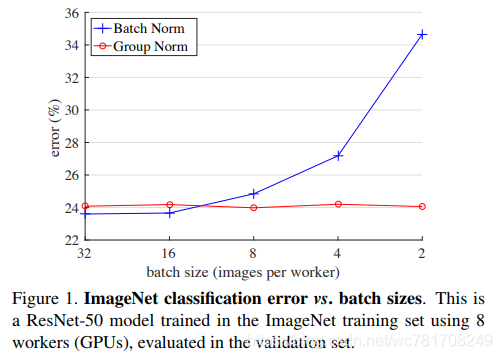
批量标准化（BN）是深度学习开发中的里程碑技术，可以使各种网络进行训练.但是，沿batch维度进行标准化会带来问题 - 当batch size变小时，BN的错误会迅速增加，这是由于batch统计估计不准确造成的.

GN将通道分成组，并在每组内计算标准化的均值和方差。GN的计算与batch size无关，并且其准确性在各种批量大小中都是稳定的.

Introduction

BN通过在(mini-)batch内计算的均值和方差对特征进行归一化。BN是许多最先进的计算机视觉算法的基础。

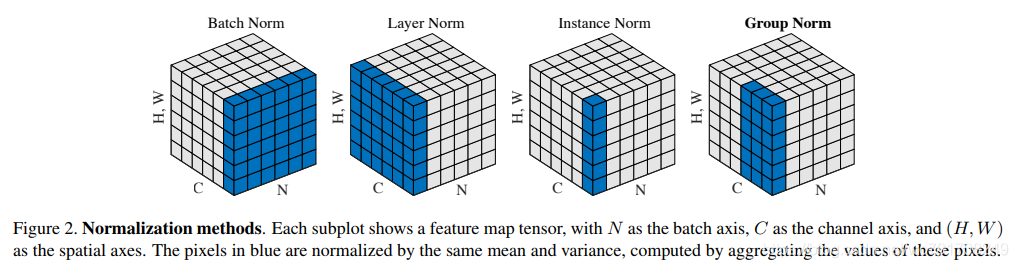
已有的方法，例如Layer Normalizatio（LN）[3]和 Instance Normalization（IN）[61]（图2），也避免了沿批量维度的标准化。

Related Work

Normalization

众所周知，对输入数据进行标准化可以使训练更快[33]。 为了标准化隐藏特征，初始化方法[33,14,19]是基于特征分布的强假设导出的，当训练发展时，这些假设可能变得无效。

深度网络中的归一化层在BN开发之前已被广泛使用。局部响应规范化（LRN）[40,28,32]是AlexNet [32]和以下模型[64,53,58]中的一个组件。 与最近的方法[26,3,61]不同，LRN计算每个像素的小邻域中的统计数据。

批量标准化[26]沿批量维度执行更多的全局标准化（并且重要的是，它建议对所有层执行此操作）。

已经提出了几种归一化方法[3,61,51,2,46]以避免利用批量维度。层标准化（LN）[3]沿 channel dimension操作，实例标准化（IN）[61]执行类似BN的计算，但仅针对每个样本（图2）。Weight Normalization（WN）[51]建议对滤波器权重进行标准化，而不是对特征进行操作。这些方法不会受到批量维度引起的问题的困扰，但是它们无法在许多视觉识别任务中接近BN的准确性。

Addressing small batches

Ioffe [25]提出了Batch Renormalization （BR），它可以减轻BN涉及小批量的问题。BR引入了两个额外的参数，这些参数限制了BN在一定范围内的估计平均值和方差，减小了批量大小时的漂移。 在小批量制度中，BR比BN具有更好的准确性。 但BR也是依赖于批次的，当批量大小减小时，其准确度仍然会下降[25]。

还有人试图避免使用small batches。 [43]中的对象检测器执行同步BN，其均值和方差是跨多个GPU计算的。但是，这种方法不能解决小批量的问题; 相反，它使用与BN要求成比例的多个GPU将算法问题迁移到工程和硬件需求

Group-wise computation

AlexNet [32]提出了用于将模型分发到两个GPU中的群组卷积。

MobileNet [23]和Xception [7]利用channel-wise（也称为“depth-wise”）卷积，这是一个群组卷积，其group number等于channel number。ShuffleNet [65]提出了一种通道混洗操作，它可以置换分组特征的轴。尽管与这些方法有关，但GN不需要组卷积。 GN是一个通用层，正如我们在标准ResNets [20]中评估的那样。

Group Normalization

例如，对于网络的conv1（第一卷积层），它是合理的期望滤波器及其水平翻转在自然图像上表现出类似的滤波器响应分布。如果conv1碰巧大约学习这对滤波器，或者如果通过设计[11,8]将水平翻转（或其他变换）制成架构，则可以将这些滤波器的相应通道一起归一化。

Formulation

我们首先描述特征归一化的一般公式，然后在该公式中呈现GN。一系列特征规范化方法（包括BN，LN，IN和GN）执行以下计算：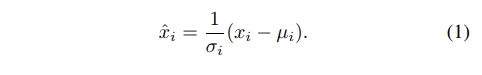
这里$x$是由层计算的特征，$i$是索引值。在2D图像的情况下，$i=(i_N,i_C,i_H,i_W)$是一个以（N，C，H，W）顺序索引特征的4D向量，N为batch axis，C为 channel axis，H and W是spatial height and width axes。

(1)式中的$\mu$和$\sigma$为均值，标准差（std）由以下公式计算得到：

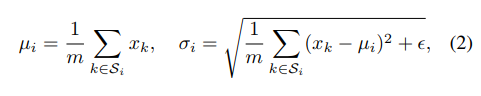
$ϵ$是一个很小的常数。$S_i$是计算mean和std的像素集，$m$是这个集合的大小。

许多类型的特征规范化方法主要有所不同在于怎么定义$S_i$(见图2)。

在Batch Norm [26]，$S_i$被定义为：

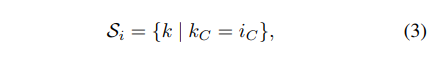
这里$i_C$（和$k_C$）表示沿C轴的i（和k）的子索引。这意味着共享相同channel索引的像素被一起归一化，对于每个通道，BN沿（N，H，W）轴计算μ和σ。

Layer Norm [3]

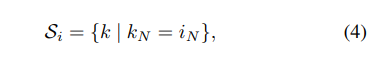
LN沿（C，H，W）轴计算μ和σ。

Instance Norm
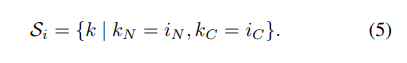[61]

IN沿（H，W）轴计算μ和σ。

如[26]中所述，BN，LN和IN的所有方法都学习了一个每通道线性变换，以补偿表示能力的可能丢失：

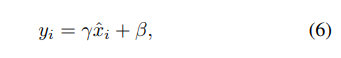
其中γ和β是可训练的比例和移位（在所有情况下由$i_C$索引，我们省略了简化符号）。

Group Norm.形式上，Group Norm层计算集合$S_i$中的μ和σ，定义为：

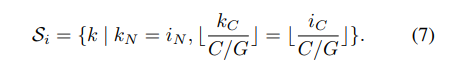
这里G为groups数，这是一个预定义的超参数(默认为G=32).$C/G$是每组的通道数.
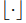是floor operation,

$\lfloor \frac{k_C}{C/G}\rfloor =\lfloor \frac{i_C}{C/G}\rfloor$意味着索引i，k是在相同的通道组，假设每组通道沿C轴按顺序存储.GN是沿(H, W)轴和$C/G$通道组计算μ和σ。

Implementation

实际上，我们只需要沿着由归一化方法定义的适当轴指定如何计算均值和方差（“moments”）。

代码实现

pytorch版本 参考：here

import torch
import torch.nn as nn


class GroupNorm(nn.Module):
    def __init__(self, num_features, num_groups=32, eps=1e-5):
        super(GroupNorm, self).__init__()
        self.weight = nn.Parameter(torch.ones(1,num_features,1,1))
        self.bias = nn.Parameter(torch.zeros(1,num_features,1,1))
        self.num_groups = num_groups
        self.eps = eps

    def forward(self, x):
        N,C,H,W = x.size()
        G = self.num_groups
        assert C % G == 0

        x = x.view(N,G,-1)
        mean = x.mean(-1, keepdim=True)
        var = x.var(-1, keepdim=True)

        x = (x-mean) / (var+self.eps).sqrt()
        x = x.view(N,C,H,W)
        return x * self.weight + self.bias

tensorflow版本 参考:here

def norm(x, norm_type, is_train, G=32, esp=1e-5):
    with tf.variable_scope('{}_norm'.format(norm_type)):
        if norm_type == 'none':
            output = x
        elif norm_type == 'batch':
            output = tf.contrib.layers.batch_norm(
                x, center=True, scale=True, decay=0.999,
                is_training=is_train, updates_collections=None
            )
        elif norm_type == 'group':
            # normalize
            # tranpose: [bs, h, w, c] to [bs, c, h, w] following the paper
            x = tf.transpose(x, [0, 3, 1, 2])
            N, C, H, W = x.get_shape().as_list()
            G = min(G, C)
            x = tf.reshape(x, [-1, G, C // G, H, W])
            mean, var = tf.nn.moments(x, [2, 3, 4], keep_dims=True)
            x = (x - mean) / tf.sqrt(var + esp)
            # per channel gamma and beta
            gamma = tf.Variable(tf.constant(1.0, shape=[C]), dtype=tf.float32, name='gamma')
            beta = tf.Variable(tf.constant(0.0, shape=[C]), dtype=tf.float32, name='beta')
            gamma = tf.reshape(gamma, [1, C, 1, 1])
            beta = tf.reshape(beta, [1, C, 1, 1])

            output = tf.reshape(x, [-1, C, H, W]) * gamma + beta
            # tranpose: [bs, c, h, w, c] to [bs, h, w, c] following the paper
            output = tf.transpose(output, [0, 2, 3, 1])
        else:
            raise NotImplementedError
    return output