Normalization

• Normalization的理解

Normalization - - “规范化”，是一种对数值的特殊函数变换方法，也就是说假设原始的某个数值是x，套上一个起到规范化作用的函数，对规范化之前的数值x进行转换，形成一个规范化后的数值f(x)。

所谓规范化，是希望转换后的数值 满足一定的特性，至于对数值具体如何变换，跟规范化目标有关，也就是说 f( ) 函数的具体形式，不同的规范化目标导致具体方法中函数所采用的形式不同。

• 为什么要Normalization
  简单的理解：生活中，让每一个学校的学生都穿上自己学校的校服，这样就可以很容易的将每个学生所属的学校区分开。

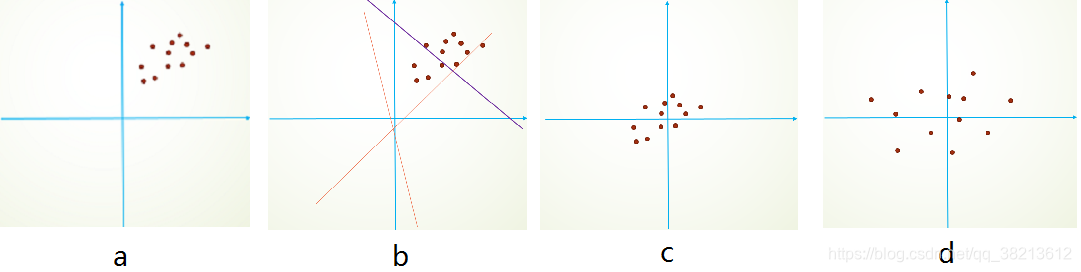
再举个简单线性分类例子，假设我们的数据分布如a所示，参数初始化一般是0均值，和较小的方差，此时拟合的y=w x+ b ，y如b图中的橘色线，经过多次迭代后，达到紫色线，此时具有很好的分类效果，但是如果我们将其归一化到0点附近，显然会加快训练速度，如此我们更进一步的通过变换拉大数据之间的相对差异性，那么就更容易区分了。

• Normalization的分类

在神经网络中，有且只有两类实例：每一层的神经元，以及连接相邻神经元之间的边。
根据对这两类不同实例的转换， 分为两种规范化的方式：

①对连接神经元边上的权重进行规范化操作：
比如Weight Norm就属于这一类；在Loss函数上加L1正则项（使矩阵更稀疏，容易计算）或L2正则项。避免模型在训练过程中过拟合

②对L层神经元的激活值进行Normalization：
如LN/BN/IN/GN/SN,今天主要整理一下这五类规范化的方法

• Normalization

对于神经元的激活值来说，不论哪种Normalization方法，其规范化目标都是一样的，就是将其激活值规整为均值为0，方差为1的正态分布。即规范化函数统一都是如下形式：

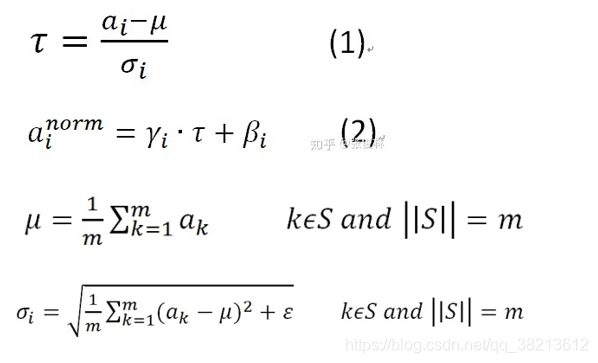
公式(2)中两个调节因子γ和β存在的目的，是为了提高式子的非线性表达能力。

因为均值和方差都是统计量，它们需要在某一个集合中计算。因此几种规范化方法中，唯一的区别就在于，它们在计算均值和方差时所选的集合不同：

如下图所示：依次为BN,LN,IN,GN

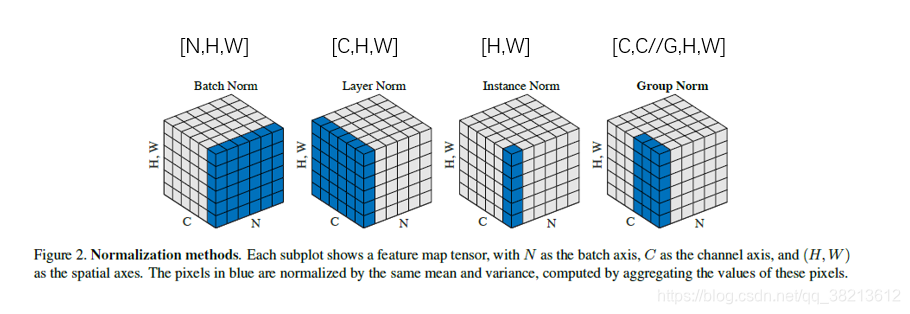
某一层神经网络来说，它的输入是[N,C,H,W]四维的

Batch Normalization
在Batch方向（N）上做规范化，每一个在batch中的Input,都选择同一channel,将这些选择好的channel放入集合S，求均值和方差。对[N,H,W]做归一化。

参考代码：

import numpy as np

def Batchnorm(x, gamma, beta, bn_param):

    # x_shape:[B, C, H, W]
    running_mean = bn_param['running_mean']
    running_var = bn_param['running_var']
    results = 0.
    eps = 1e-5

    x_mean = np.mean(x, axis=(0, 2, 3), keepdims=True)
    x_var = np.var(x, axis=(0, 2, 3), keepdims=True0)
    x_normalized = (x - x_mean) / np.sqrt(x_var + eps)
    results = gamma * x_normalized + beta

    # 因为在测试时是单个图片测试，这里保留训练时的均值和方差，用在后面测试时用
    running_mean = momentum * running_mean + (1 - momentum) * x_mean
    running_var = momentum * running_var + (1 - momentum) * x_var

    bn_param['running_mean'] = running_mean
    bn_param['running_var'] = running_var

    return results, bn_param

Layer Normalization

与BN不同，LN是针对深度网络的某一层的所有神经元的输入按以下公式进行normalize操作。抛除了Batch的概念，在[C,H,W]上做归一化操作。

def Layernorm(x, gamma, beta):

    # x_shape:[B, C, H, W]
    results = 0.
    eps = 1e-5

    x_mean = np.mean(x, axis=(1, 2, 3), keepdims=True)
    x_var = np.var(x, axis=(1, 2, 3), keepdims=True)
    x_normalized = (x - x_mean) / np.sqrt(x_var + eps)
    results = gamma * x_normalized + beta
    return results


**Group Normalization**

BN对batchsize的大小比较敏感，由于每次计算均值和方差是在一个batch上，所以如果batchsize太小，则计算的均值、方差不足以代表整个数据分布；所以提出了GN这种改进方法：

def GroupNorm(x, gamma, beta, G=16):

# x_shape:[B, C, H, W]
results = 0.
eps = 1e-5
x = np.reshape(x, (x.shape[0], G, x.shape[1]/16, x.shape[2], x.shape[3]))

x_mean = np.mean(x, axis=(2, 3, 4), keepdims=True)
x_var = np.var(x, axis=(2, 3, 4), keepdims=True0)
x_normalized = (x - x_mean) / np.sqrt(x_var + eps)
results = gamma * x_normalized + beta
return results

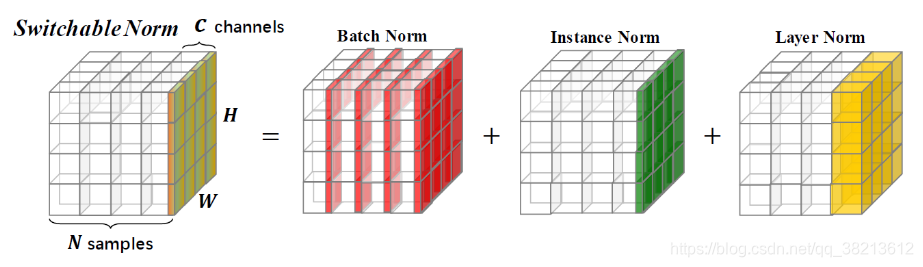
Switchable Normalization

SN就是对BN,IN,LN的均值和方差加权之后再求自己的均值和方差。
至于权重，让网络自己在不同的模型和任务中自行学习。

def SwitchableNorm(x, gamma, beta, w_mean, w_var):
    # x_shape:[B, C, H, W]
    results = 0.
    eps = 1e-5

    mean_in = np.mean(x, axis=(2, 3), keepdims=True)
    var_in = np.var(x, axis=(2, 3), keepdims=True)

    mean_ln = np.mean(x, axis=(1, 2, 3), keepdims=True)
    var_ln = np.var(x, axis=(1, 2, 3), keepdims=True)

    mean_bn = np.mean(x, axis=(0, 2, 3), keepdims=True)
    var_bn = np.var(x, axis=(0, 2, 3), keepdims=True)

    mean = w_mean[0] * mean_in + w_mean[1] * mean_ln + w_mean[2] * mean_bn
    var = w_var[0] * var_in + w_var[1] * var_ln + w_var[2] * var_bn

    x_normalized = (x - mean) / np.sqrt(var + eps)
    results = gamma * x_normalized + beta
    return results