数据分析与处理（二）线性判别分析（LDA）

线性判别分析

  之前分析了主成分分析，是一种线性的降维方法，今天再来分析一下线性判别分析。
  PCA和LDA都是线性的降维方法，PCA是无监督的，它没有考虑样本数据的标签；LDA是有标签的，它考虑样本的标签，并致力于让样本数据可分性最大化。二者都用于数据降维，而且经常一起使用。

原理

  在做分类算法的时候，我们的准则是要让类间距离尽可能大，类内距离尽可能小。LDA用于分类问题，假设我们现在有一个分类问题，共有C个类，每个类有$N_i$个m维的样本，对于${\omega }_i$类而言，它的数据集定义如下：
{ x 1 , x 2 , . . . , x N i } \{x^1,x^2,...,x^{N_i}\} {x1,x2,...,xNi​}
我们希望能够找到一种映射，将原始数据X映射到Y，Y位于一个C-1维的超平面上。
以两类问题为例， ω 1 : { x 1 , x 2 , . . . , x N 1 } \omega_1:\{x^1,x^2,...,x^{N_1}\} ω1​:{x1,x2,...,xN1​},
ω 2 : { x 1 , x 2 , . . . , x N 2 } \omega_2:\{x^1,x^2,...,x^{N_2}\} ω2​:{x1,x2,...,xN2​}
利用变换矩阵w，我们希望将x投影到一维坐标上，也就是一个数值，对此，我们有
$$y=w^{T}x$$
w是m*1的列向量，我们需要将y的可分性最大化。
对于x，我们有
$${\mu }_i=\frac{1}{N_i}\sum _{x\in {\omega }_i}x$$
对于y，我们有
$$\tilde{\mu }=\frac{1}{N_i}\sum _{y\in {\omega }_i}y=\frac{1}{N_i}\sum _{x\in {\omega }_i}{w}^{T}x=w^T\frac{1}{N_i}\sum _{x\in {\omega }_i}x=w^T{\mu }_i$$
投影后的类间均值距离为
$$J(w)=|\widetilde{{\mu }_1}-\widetilde{{\mu }_2}|=|w^T{\mu }_1-w^T{\mu }_2|=|w^T({\mu }_1-{\mu }_2)|$$
这个距离存在一定的局限性，因为它没有考虑类内的方差，改进的办法是引入类内标方。
对于投影后的y，我们有
$${\widetilde{s_i}}^2=\sum _{y\in {\omega }_i}{(y-\widetilde{{\mu }_i})}^2$$
我们用${\widetilde{s_1}}^2$和${\widetilde{s_2}}^2$来衡量投影后类间的方差。
修正后的类间距离为
$$J(w)=\frac{|\widetilde{{\mu }_1}-\widetilde{{\mu }_2}{|}^2}{{\widetilde{s_1}}^2+{\widetilde{s_2}}^2}$$
这和我们的直觉是相符合的，我们需要让投影后的类间距离最大，而类内距离最小，这和上式的分子和分母是相对应的。
类内协方差矩阵如下：
$$S_i=\sum _{x\in {\omega }_i}(x-{\mu }_i)(x-{\mu }_i{)}^T$$
类内散布矩阵如下：
$$S_w=S_1+S_2$$
基于此，有
$$\begin{gathered} {\widetilde{s_i}}^2=\sum _{y\in {\omega }_i}(y-\tilde{\mu }{)}^2 \\ =\sum _{x\in {\omega }_i}(w^{T}x-w^T{\mu }_i{)}^2 \\ =\sum _{x\in {\omega }_i}{w}^T(x-{\mu }_i)(x-{\mu }_i{)}^{T}w \\ =w^T(\sum _{x\in {\omega }_i}(x-{\mu }_i)(x-{\mu }_i{)}^T)w \\ =w^T{S}_{i}w \end{gathered}$$
然后，
$$\begin{gathered} {\widetilde{s_1}}^2+{\widetilde{s_2}}^2=w^T{S}_{1}w+w^T{S}_{2}w \\ =w^T(S_1+S_2)w \\ =w^T{S}_{w}w \\ =\widetilde{S_w} \end{gathered}$$

$$\begin{gathered} |\widetilde{{\mu }_1}-\widetilde{{\mu }_2}{|}^2=(w^T{\mu }_1-w^T{\mu }_2{)}^2 \\ =w^T({\mu }_1-{\mu }_2)({\mu }_1-{\mu }_2{)}^{T}w \\ =w^T{S}_{B}w \\ =\widetilde{S_B} \end{gathered}$$
$S_B$为类间散布矩阵。
$$J(w)=\frac{|\widetilde{{\mu }_1}-\widetilde{{\mu }_2}{|}^2}{{\widetilde{s_1}}^2+{\widetilde{s_2}}^2}=\frac{w^T{S}_{B}w}{w^T{S}_{w}w}$$
为了使J(w)最小，我们需要对其进行求导，我们要找到一个w，使得上式最大
d d x J ( w ) = d d w { w T S B w w T S w w } = 0 \frac{\mathrm{d}}{\mathrm{d}x}J(w)=\frac{\mathrm{d}}{\mathrm{d}w}\{\frac{w^TS_Bw}{w^TS_ww}\}=0 dxd​J(w)=dwd​{wTSw​wwTSB​w​}=0
即需要让求导后的分子为0，
{ w T S w w } d d w { w T S B w } − { w T S B w } d d w w T S w w = 0 \{w^TS_ww\}\frac{\mathrm{d}}{\mathrm{d}w}\{w^TS_Bw\}-\{w^TS_Bw\}\frac{\mathrm{d}}{\mathrm{d}w}{w^TS_ww}=0 {wTSw​w}dwd​{wTSB​w}−{wTSB​w}dwd​wTSw​w=0
即，
$$(w^T{S}_{w}w)2S_{B}w-(w^T{S}_{B}w)2S_{w}w=0$$
两边同时除以$2w^T{S}_{w}w$,得到
$$\frac{w^T{S}_{w}w}{w^T{S}_{w}w}{S}_{B}w-\frac{w^T{S}_{B}w}{w^T{S}_{w}w}{S}_{w}w=0$$
$$\to S_{B}w-J(w)S_{w}w=0$$
$$\to S_w^{-1}{S}_{B}w-J(w)w=0$$
解上式得，
$$S_w^{-1}{S}_{B}w=\lambda w$$
这就是我们熟悉的特征值了。
于是，
w ∗ = arg ⁡ max ⁡ w J ( w ) = arg ⁡ max ⁡ w { w T S B w w T S w w } w^*= \arg \max _wJ(w)=\arg \max _w\{\frac{w^TS_Bw}{w^TS_ww}\} w∗=argwmax​J(w)=argwmax​{wTSw​wwTSB​w​}
w是$S_w^{-1}{S}_B$的最大特征值对应的特征向量。

多类的情况

  之前我们讨论了两类时的情况，下面我们将扩展到多类时的情形，分析是类似的。
  假定我们目前有C个类，我们需要C-1个向量，将原始数据映射到C-1维的超平面上。转换矩阵为$W=[w_1,w_2,...,w_{C-1}]$,$y_i=w_i^{T}x$,x是m1的向量，y是c1的向量，W是m*(C-1)的矩阵。
假设数据集大小为n，每组数据有m个特征，则上式可以表示如下：
$$Y=W^{T}X$$
$$X_{m\ast n}=\left[\begin{array}{cccc}{x}_1^1& x_1^2& \cdots & x_1^n\\ ⋮& ⋮& ⋮& ⋮\\ x_m^1& x_m^2& \cdots & x_m^n\end{array}\right]$$
$$Y_{C-1\ast n}=\left[\begin{array}{cccc}{y}_1^1& y_1^2& \cdots & y_1^n\\ ⋮& ⋮& ⋮& ⋮\\ y_{C-1}^1& y_{C-1}^2& \cdots & y_{C-1}^n\end{array}\right]$$
$$W_m^{C-1}=[w_1,w_2,...,w_{C-1}]$$
类内散布矩定义如下：
$$S_w=\sum _{i=1}^C{S}_i$$
$$S_i=\sum _{x\in {\omega }_i}(x-{\mu }_i)(x-{\mu }_i{)}^T$$
$${\mu }_i=\frac{1}{N_i}\sum _{x\in {\omega }_i}x$$
类间散布矩阵定义如下：
$$S_B=\sum _{i=1}^C{N}_i({\mu }_i-\mu )({\mu }_i-\mu {)}^T$$
$$\mu =\frac{1}{N}\sum _{\forall x}x=\frac{1}{N}\sum _{i=1}^C{N}_i{\mu }_i$$
$${\mu }_i=\frac{1}{N_i}\sum _{x\in {\omega }_i}x$$
同样的，对于y，我们有
$$\widetilde{{\mu }_i}=\frac{1}{N_i}\sum _{y\in {\omega }_i}y$$
$$\tilde{\mu }=\frac{1}{N}\sum _{\forall y}y$$
$$\widetilde{S_w}=\sum _{i=1}^C\widetilde{S_i}=\sum _{i=1}^C\sum _{y\in {\omega }_i}(y-\widetilde{{\mu }_i})(y-\widetilde{{\mu }_i}{)}^T$$
$$\widetilde{S_B}=\sum _{i=1}^C{N}_i(\widetilde{{\mu }_i}-\tilde{\mu })(\widetilde{{\mu }_i}-\tilde{\mu }{)}^T$$
再来计算J(w),
$$\widetilde{S_w}=W^T{S}_{w}W$$
$$\widetilde{S_B}=W^T{S}_{B}W$$
$$J(w)=\frac{|\widetilde{S_B}|}{|\widetilde{S_w}|}=\frac{|W^T{S}_{B}W|}{|W^T{S}_{w}W|}$$
此时的类间散布矩阵已经不是数值了，所以我们取了它的行列式的值。
依然用求导的方法，我们可以得到，
$$S_w^{-1}{S}_B{w}_i={\lambda }_i{w}_i$$
$${\lambda }_i=J(w_i)$$
于是，转换矩阵W是由$S_w^{-1}{S}_B$的前C-1大的特征值对应的特征向量组成的。

局限性

• LDA也有它自身的局限性，它最多只能提供C-1维的特征映射，如果需要更多的特征就不能采用LDA了。
• LDA假定样本数据服从的是高斯分布，如果样本服从的不是高斯分布，则LDA不再成立。
• 当样本的判别信息不是均值而是方差的时候，LDA会失效。举个极端的例子就是当不同类别的样本数据的均值相同的时候，这是它们的类间距离都为0，经过线性映射后的Y的类间距离也为0，J(w)就没有意义了。

实验效果

python sklearn中有LDA的模块，可以直接利用它来进行线性判别分析，我们采用鸢尾花数据进行测试。
代码如下：

from sklearn.datasets import load_iris
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.model_selection import train_test_split
import numpy as np
iris_data=load_iris()
X=iris_data['data']
y=iris_data['target']
#print(X.shape) # (150,4)
#print(y.shape) #(150,)
# print(y)
lda=LinearDiscriminantAnalysis()
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.3,random_state=0,stratify=y)
# print(X_train.shape)
# print(X_test.shape)
lda.fit(X_train,y_train)
print(lda.coef_)
print(lda.intercept_)
print(lda.score(X_test,y_test))
X_transformed=np.dot(X_train,lda.coef_.transpose(1,0))
# print(X_transformed.shape) #(150,3)
fig=plt.figure()
ax=Axes3D(fig,rect=[0,0,1,1],elev=30,azim=20)
colors=['r','g','b','yellow']
for i in range(X_transformed.shape[0]):
    ax.scatter(X_transformed[i][0],X_transformed[i][1],X_transformed[i],color=colors[y_train[i]],marker='*')
plt.show()

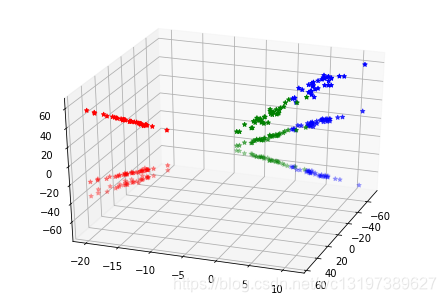
采用的是jupyter notebook，降维后的样本分布如下：

参考资料

• pdf文件