素数
1.基础知识
100以内的质数有:2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97共
25个;
20以内的质数有:2,3,5,7,11,13,17,19;共8个;

按照如上定义,不难写出如下代码来判断一个数是否为素数。
bool isPrime(long long n){
if(n<=3) return n>1; // 2和3均视作质数,1不为质数
else if(n % 2 == 0 || n % 3 == 0) return false; // 存在因子2或3,则不为质数
else{
// 依次判断,直到sqrt(n)
for(int i=4;i*i<=n;i++){
if(n%i==0){
return false;
}
}
return true;
}
}
另外,所有大于3的素数都可以表示为6N-1或者6N+1(被称为孪生素数)。因此,可通过判断是否能被大于3的质因子整除进行优化,如下:
bool isPrime(unsigned long long n) {
if (n <= 3) {
return n > 1;
} else if (n % 2 == 0 || n % 3 == 0) {
return false;
} else {
// 优化,判断是否能被大于3的质因子整除
for (unsigned short i = 5; i * i <= n; i += 6) {
if (n % i == 0 || n % (i + 2) == 0) {
return false;
}
}
return true;
}
}
2.例题
2.1 素数对
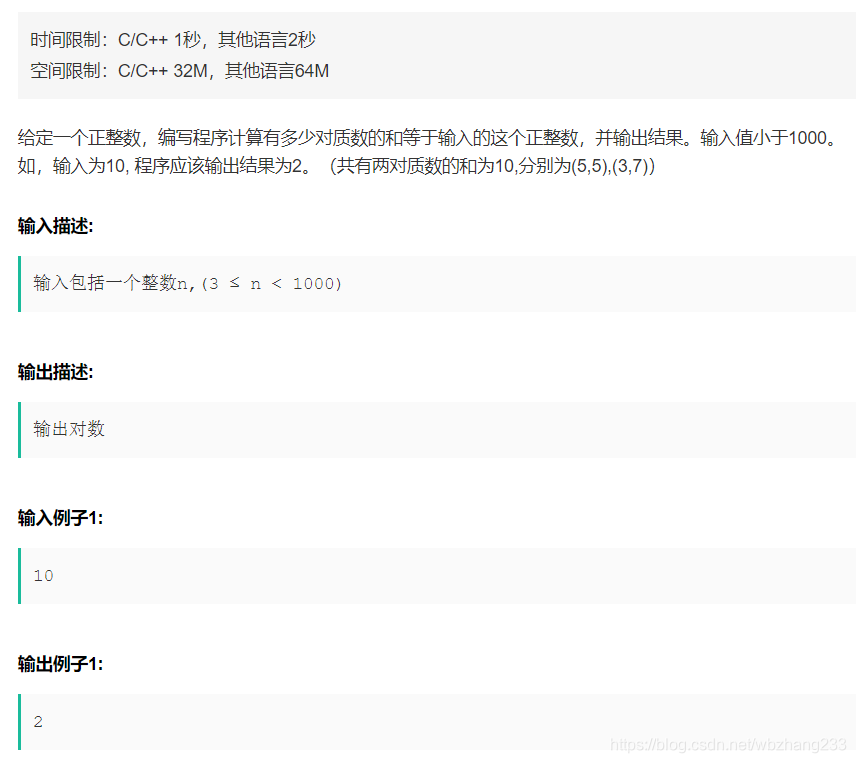
筛选法求素数。
#include <iostream>
#include <vector>
using namespace std;
int main(){
//筛选法求素数(删除所有素数的倍数)
vector<int> v(1000,1);
for(int i=2;i<1000;++i){
for(int j=2;i*j<1000;++j){
if(v[i]){
v[i*j]=0;
}
}
}
int x;
cin>>x;
int res=0;
for(int i=2;i<=x/2;++i){
if(v[i]&&v[x-i]) ++res;
}
cout<<res<<endl;
}
2.2 质数因子
来源:华为笔试题
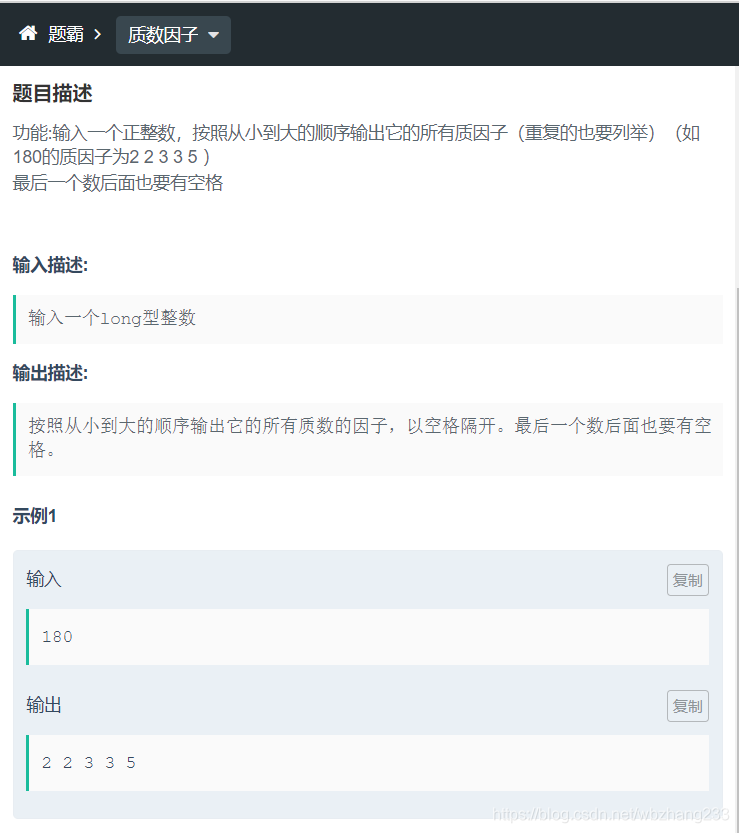
解题思路: 首先确定正整数的范围,明确几点特判(数很小的时候),否则依次求其质因子。
- x<=3,返回x>1
- 分解因子2和因子3
- 分解大于3的因子
- 如果结果中无因子,则为质数;返回{x}本身
- 如果最后结果为1,则
以下为AC代码:
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
vector<long> getPrime(long x)
{
if(x<=3) return {x};
vector<long> res;
//假设x为合数,则按以下顺序分解
// 获得2、3的质因子
while(x%2==0){
x=x/2;
res.push_back(2);
}
while(x%3==0){
x = x/3;
res.push_back(3);
}
if(x>=5){
// 大于3的质数均为6N-1或者6N+1
for(int i=5;i*i<=x;i+=6){
while( x%i==0){
x=x/i;
res.push_back(i);
}
while(x%(i+2)==0){
x=x/(i+2);
res.push_back(i+2);
}
// 这一对孪生素数分解完之后,x若大于i*i,将继续分解;否则必然为小于i*i的质数
// 反证:如果x为合数,则其因子不可能比先前分解的质因子要大(不然肯定被分解了),因此其因子比此前的所有质因子都大。
}
}
if(res.size()==0)
return {x}; //无法分解,表明x为质数
if(x!=1) res.push_back(x); //最后存在的质因子
return res;
}
int main()
{
long x;
cin>>x;
vector<long> res= getPrime(x);
for(auto ele:res){
cout<<ele<<" ";
}
return 0;
}
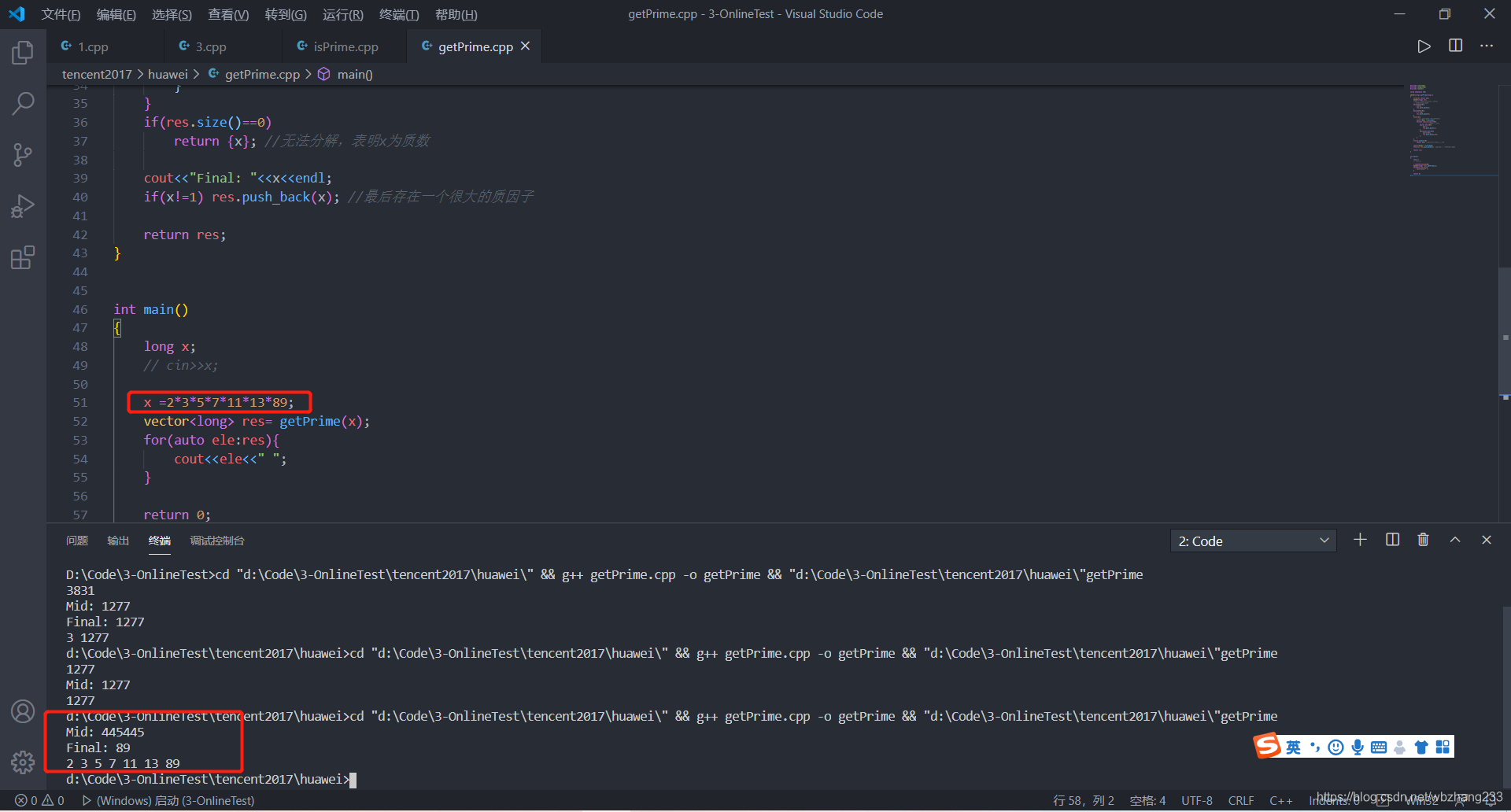
实测如下:





 本文深入探讨素数的基本概念,提供高效的素数判断算法,包括优化的试除法及筛选法,并通过实例讲解素数对与质数因子的求解方法。
本文深入探讨素数的基本概念,提供高效的素数判断算法,包括优化的试除法及筛选法,并通过实例讲解素数对与质数因子的求解方法。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








