【开源社区openEuler实践】 D2. Mocha and Diana (Hard Version)

题目

思路：

性质1：能在结点u，v添加边的充要条件是u，v在第一个图和第二个图都不连通

性质2：可以添加的边数等于 n - 1 - max(m1, m2)，并且添加边的顺序不会影响结果（即 边（u，v）满足性质1，就可以直接添加，不会影响结果），证明如下：

        

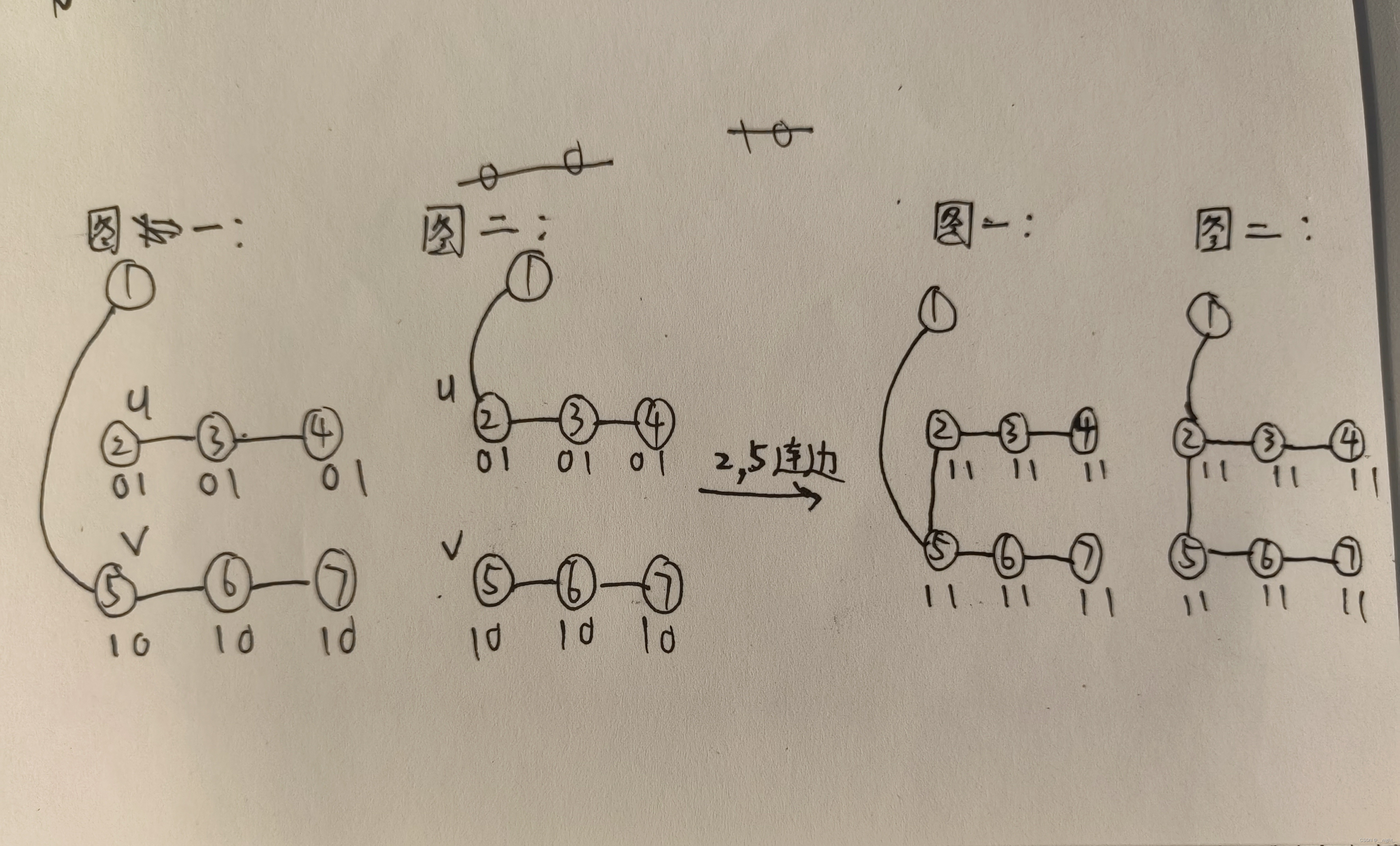
对于hard version：先让所有可以与结点1连边的结点连边，然后对于结点2 ~ n，可以分为三类结点：在第一个图与结点1不连通，在第二个图与结点1连通（表示为01）、10 、11，（不存在00，若存在00，那么这个结点就会与结点1连边，变成11）。11的结点不能再连边，对答案无贡献，可以忽略；01的结点u可以与10的结点v连边，注意添加边（u，v）后，原本和u在第一个图中同一个连通块的结点（原本整个连通块的结点都是01）都会变成11，同理v在第二个图中所在连通块也是变成11，故对于每个连通块只找最高级祖先来连边。