数字图像处理第五章-图像复原与重建

目录

5.1图像退化/复原过程的模型

5.2噪声模型

5.2.1噪声的空间和频率特性

5.2.2一些重要的噪声概率密度函数

5.2.3周期噪声

5.2.4噪声参数额估计

5.3只存在噪声的复原

5.3.1均值滤波器

5.3.2统计排序滤波器

5.3.3自适应滤波器

5.4 用频率域滤波消除周期噪声

5.4.1带阻滤波器

5.4.2带通滤波器

5.4.3陷波滤波器

5.4.4最佳陷波滤波器

5.5线性，位置不变的退化

5.6估计退化函数5.6.1图像观察估计

5.6.2试验估计

5.6.3建模估计

5.7逆滤波

5.8最小均方误差滤波

5.9约束最小乘方滤波

5.10几何均值滤波

---

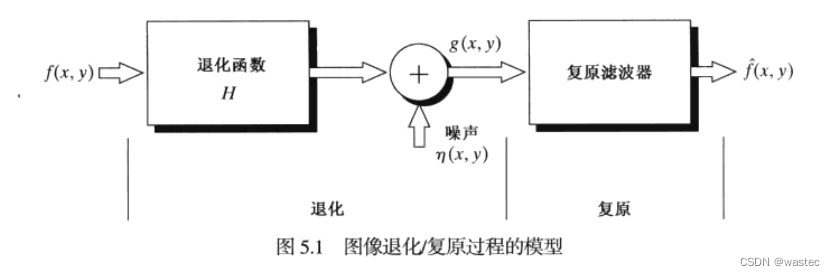
5.1图像退化/复原过程的模型

如果H是一个线性的、位置不变的过程，那么空间域中的退化图像可由下式给出：        
                                

其中，h(x,y)是退化函数的空间表示；空间域中的卷积等同于频率域中的乘积，因此可以把上式中的模型写成等价的频率域表示：

                ​​​​​​​        ​​​​​​​        ​​​​​​​   

        

5.2噪声模型

5.2.1噪声的空间和频率特性

        频率特性是指傅里叶域中噪声的频率内容(即相对于电磁波谱的频率)。例如，当噪声的傅里叶谱是常量时，噪声通常称为白噪声。这个术语是从白光的物理特性派生出来的，它以相等的比例包含可见光谱中的几乎所有频率。

5.2.2一些重要的噪声概率密度函数

高斯噪声：

高斯随机变量z的PDF由下式给出：

瑞利噪声：

瑞利噪声的PDF由下式给出：

爱尔兰（伽马噪声）：

爱尔兰噪声的PDF由下式给出：
 

指数噪声：

指数噪声的PDF由下式给出：

均匀噪声：

均匀噪声的PDF由下式给出：

脉冲(椒盐)噪声
(双极)脉冲噪声的PDF由下式给出：

5.2.3周期噪声

一幅图像中的周期噪声是在图像获取期间由电力或机电干扰产生的。例如，考虑图5.5(a)中的图像。这幅图像被不同频率的(空间)正弦噪声严重干扰了。一个纯正弦波的傅里叶变换是位于正弦波共轭频率处的一对共轭脉冲(见表4.3)。因此，如果空间域中正弦波的振幅足够强，我们在该图像的谱中将看到图像中每个正弦波的脉冲对。如图5.5(b)所示。

5.2.4噪声参数额估计

典型地，周期噪声的参数是通过检测图像的傅里叶谱来估计的。当仅有通过传感器生成的图像可用时，通常可由合理的恒定灰度值的一小部分来估计PDF的参数。例如，图5.6所示的垂直条带(150×20像素)是从图5.4中所示的高斯、瑞利和均匀图像中截取的。所显示的直方图是使用这些小条带的图像数据计算出来的。与图5.6中的直方图对应的图5.4中的直方图，是图5.4(d)、图5.4(e)和图5.4(k)这三组直方图中间的一组。我们可以看出，这些对应的直方图的形状非常接近于图5.6中的直方图的形状。由于缩放的原因，它们的高度不同，但形状明显类似。

5.3只