数字图像处理第四章-频率域滤波-优快云博客

本文链接：https://blog.youkuaiyun.com/wastec/article/details/140052822

4.1基本概念

4.3.1由取样后的函数连续变换得到DFT

4.8.5钝化模版，高提升滤波和高频强调滤波

4.1基本概念

4.1.1复数

复数C的定义如下：
C=R+jl

共轭复数C*定义如下：

C*=R-jI

有时，在极坐标下表示复数很有用：
C=|C|(cosθ+jsinθ)

其中， $|C|=\sqrt{R^{2}+I^{2}}$ 是复平面的原点到点(R,I)的向量的长度，θ是该向量与实轴的夹角。

4.1.2傅里叶计数

具有周期T的连续变量t的周期函数ft)可以被描述为乘以适当系数的正弦和余弦和。我们知道，这个和就是傅里叶级数，它具有如下形式：

$f(t)=\sum_{n=-\infty }^{\infty }C_{n}e^{j\frac{2\pi n}{T}t}$ ;

其中， $C_{n}=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)e^{-j\frac{2\pi n}{T}t}dt$ ,n=0,-+1,-+2.......

4.1.3冲激及其取样特征

线性系统和傅里叶变换研究的核心是冲激及其取样特性。连续变量t在t=0处的单位冲激表示为δ(t),其定义是：

$\delta(t) \begin{cases} \ \infty , t=0 \\ & 0, t\neq 0 \end{cases}$

假设f(t)在t=0处是连续的，取样特性的一种更为一般的说明涉及位于任意点t。的冲激，表示为δ(t-to)。在这种情况下，取样特性变为:

$\int_{-\infty }^{\infty }f(t-t_{0})\delta (t)dt=f(t_{0})$

图4.3显示了一个冲激串。冲激可以是连续的或离散的。

4.1.4连续变量函数的傅里叶变换

由 $\Im$ {f(t)}表示的连续变量t的连续函数f(t)的傅里叶变换由下式定义：

$\Im \left \{ f(t)\right \}=\int_{-\infty }^{\infty }f(t)e^{-j2\pi \mu t}dt$

t可以表示任何连续变量，频率变量μ的单位取决于t的单位。例如，如果t表示单位为秒的时间，则μ的单位为周/秒，或者赫兹(Hz)。如果t表示的是以米为单位的距离，则μ的单位是周/米，等等。换句话说，频率域的单位是独立于输入变量的每单位周期的。

4.2.5卷积

卷积定义如下：

$f(t)\bigstar h(t)=\int_{-\infty }^{\infty }f(\iota )h(t-\iota )d\iota$

其中，负号表示刚刚提及的翻转，t是一个函数滑过另一个函数的位移，而 $\iota$ 是积分假变量。现在我们假定函数从-无穷扩展到+无穷。

4.2取样和取样函数的傅里叶变换

4.2.1取样

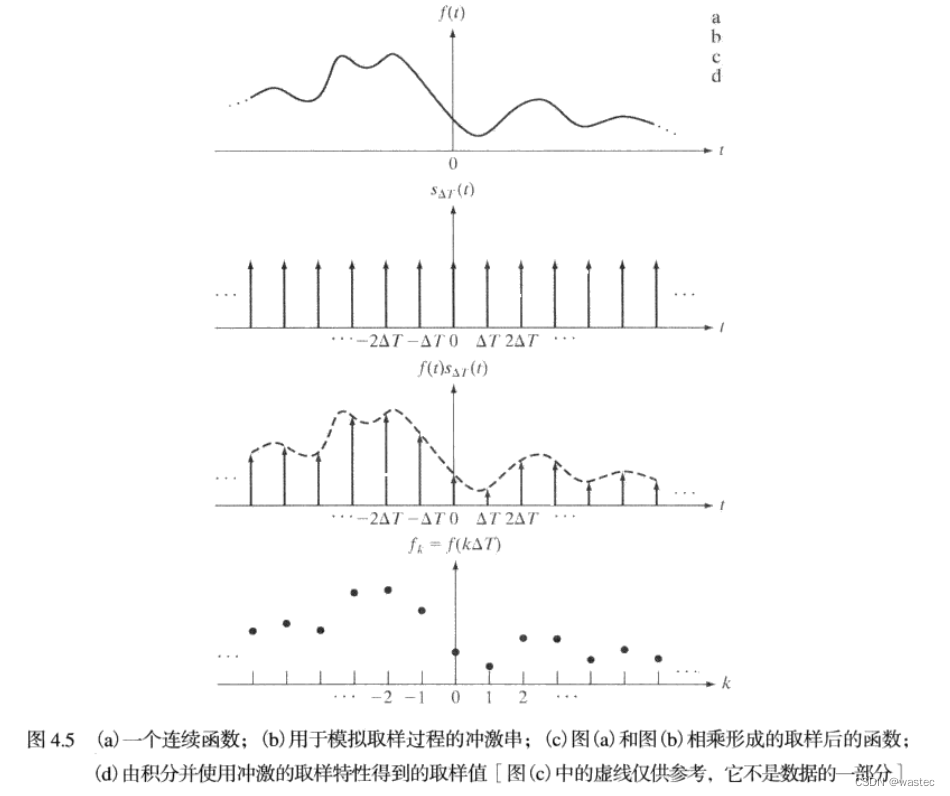
参考图4.5，考虑一个连续函数f(t),我们希望以独立变量t的均匀间隔(△T)取样。我们假定函数对于t从-无穷到+无穷扩展。模拟取样的一种方法是用一个△T单位间隔的冲激串作为取样函数去乘以f(t),即：

$\tilde{f}(t)=f(t)s_{\bigtriangleup T}(t)=\sum_{n=-\infty }^{\infty }f(t)\delta (t-n\bigtriangleup T)$

如图4.5(c)所示。每个取样值由加权后的冲激“强度”给出，我们可通过积分得到它。也就是，序列中的任意样式值 $f_{k}$ 由下式给出：

$f_{k}=\int_{-\infty }^{\infty }f(t)\delta (t-k\bigtriangleup T)dt=f(k\bigtriangleup T)$

其中，我们利用了式(4.2-10)中δ的取样特性。式(4.3-2)对任何整数k=…,-2,-1,0,1,2,…都成立。图4.5(d)显示了结果，它由原始函数的等间隔取样组成。

4.2.2取样函数的傅里叶变换

取样函数 $\tilde{f}(t)$ 的傅里叶变换 $\tilde{F(\mu )}$ 是

$\tilde{F}=\Im { \tilde{f}(t) }=\Im \left \{ f(t)s_\bigtriangleup T(t){} \right \}=F(\mu )\bigstar S(\mu )$

图4.6是前面结果的一个图示总结。图4.6(a)是函数f(t)的傅里叶变换F(μ)的简图，图4.6(b)显示了取样后的函数的变换F(μ)。在图4.6(c)中，取样率刚好足以保持F(μ),但在图4.6(d)中，取样率低于保持不同F(μ)拷贝的最小取样率要求，这样，就不能保持原始变换。

4.2.3取样定理

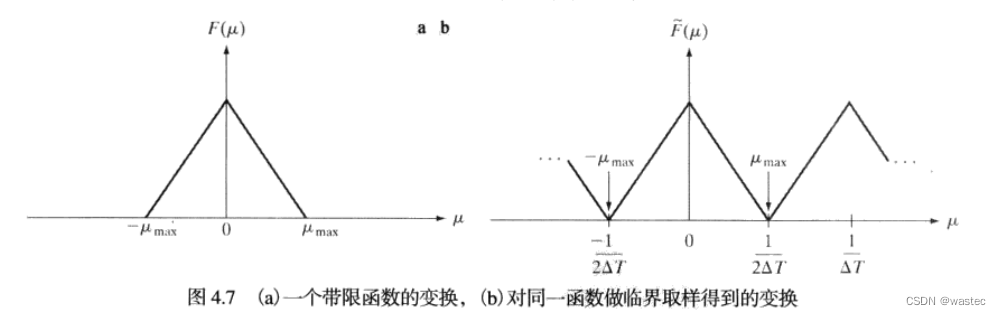
对于以原点为中心的有限区间(带宽)[-μmax,μmax]之外的频率值，其傅里叶变换为零的函数f(t)称为带限函数。图4.7(a)就是这样一个函数，它是图4.6(a)的一个放大部分。类似地，图4.7(b)是
图4.6(c)所示临界取样后的函数的傅里叶变换更详细的视图。较低的1/△T值将导致F(μ)中的周期融合，较高的1/△T值在周期之间会提供更为清晰的间隔。

4.2.4混淆

使用图4.9(b)中的理想低通滤波器，将会得到如图4.9(c)所示的一个变换，该变换已被来自邻近周期的频率破坏了。然后，反变换会产生t的一个破坏了的函数。由函数欠取样导致的这种效果就是周知的频率混淆，或简称为混淆。在字面上，混淆是一个过程，在这一过程中，一个连续函数的高频分量在取样后的函数中用低频“化妆”了。