焊接机器人离线误差补偿

船体焊接中工业机器人的离线编程误差补偿

摘要

本文针对工业机器人在船体焊接应用中的柔顺性建模与误差补偿进行了研究。采用虚拟弹簧法推导了笛卡尔刚度矩阵，该方法考虑了驱动与结构刚度、臂部重力以及外部载荷的影响。基于所建立的刚度模型，提出了一种补偿柔顺性误差的方法，并通过工业机器人沿焊接轨迹的实例进行了说明。结果表明，该补偿方法能够有效提高机器人的操作精度，使带有辅助负载的机器人实际轨迹与目标轨迹基本一致。

关键词 ：工业机器人 · Hull焊接 · Kinetostatics · Gravity效应 · Error compensation

1 引言

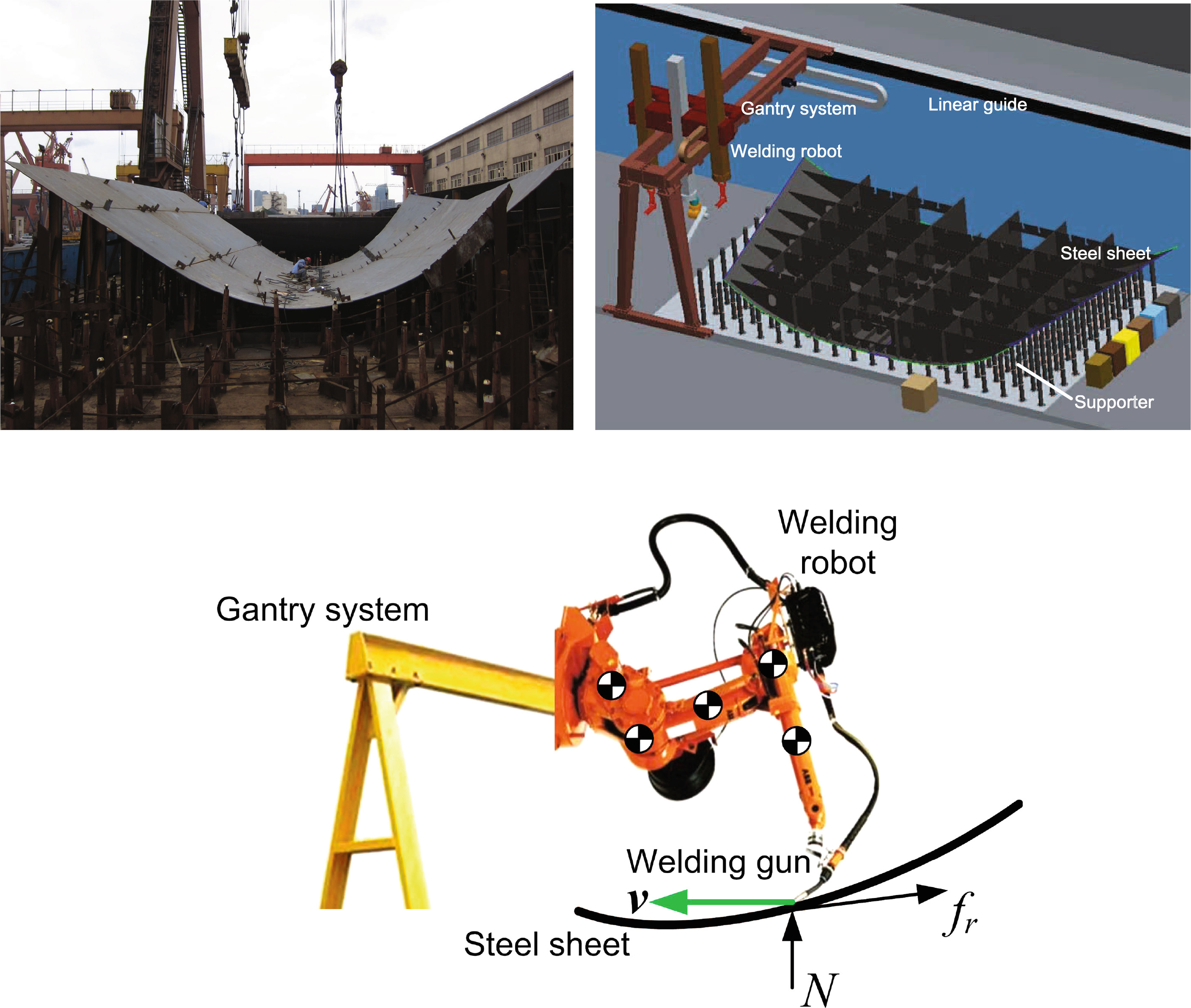
作为一种自动化制造设备，工业机器人凭借其高重复精度和操作稳定性，已在工业应用的许多领域得到广泛应用并发挥着重要作用。在这些工业应用中，此类串联操作机非常适用于焊接行业[3],例如汽车行业。此外，机器人还可用于造船行业，即大型船体焊接，如图1所示。在此过程中，焊接轨迹首先由视觉系统检测，轨迹数据将被传输至控制系统进行机器人编程，以完成焊接过程。这意味着机器人将执行一项离线任务。

机器人的运动通常通过机器人控制器利用逆运动学模型生成，以计算执行器的输入信号，从而实现期望的末端执行器位置，但该过程忽略了柔顺性误差。另一方面，如图1(c)所示，在特定外部载荷下，特别是臂部重力和动态惯性力作用下，由于机器人部件的有限强度导致弹性柔顺误差，使得运动学控制不再适用[12],即实际轨迹将偏离期望路径，导致产品质量下降，因此在应用中需要高精度。

柔顺性误差，即机器人末端执行器的几何变化，可通过标定进行补偿 [7,21],然而，该技术有时成本较高。一种经济型方法来处理误差补偿问题是修正机器人控制方案[6,10]该方案定义了笛卡尔空间中的预定轨迹：基于误差模型，重新生成有载荷的输入轨迹，以实现输出轨迹与期望轨迹的一致，而输入轨迹则不同于目标轨迹。输入轨迹的修正应基于柔度误差建模，这需要计算刚度矩阵[8]串联机器人的刚度矩阵最初由Salisbury推导得出[15],其中仅考虑了一维线性弹簧描述的驱动柔顺性。该方法中，刚度的推导基于假设机械手处于无负载平衡构型。实际上，

外部载荷直接影响机械手的平衡构型，并可能改变其刚度特性[2,4]。因此，应考虑由于外部载荷和重力引起的结构柔度和机器人几何结构的变化[11,13,14]。因此，本工作聚焦于能够考虑外部力矩、内部力矩以及机器人自重对刚度矩阵和弹性变形影响的柔顺误差建模与补偿。

本文研究了工业机器人在船体焊接中的刚度建模及柔顺性误差补偿。在负载构型下计算了笛卡尔刚度矩阵，同时考虑了驱动和结构刚度以及臂部重力和外部载荷的影响。提出了一种通过修改输入轨迹实现误差补偿的方法。该方法以焊接机器人沿一条轨迹运动为例进行了数值验证，结果表明了该误差补偿方法的有效性。

2 工业焊接机器人

图2显示了 ABB IRB4600 60/205 机器人 [1]作为本项目中的焊接机器人。IRB 4600 系列是 ABB 机器人公司新一代尖端产品的先驱，具备增强和全新的功能，其中一项工业应用专门用于焊接。

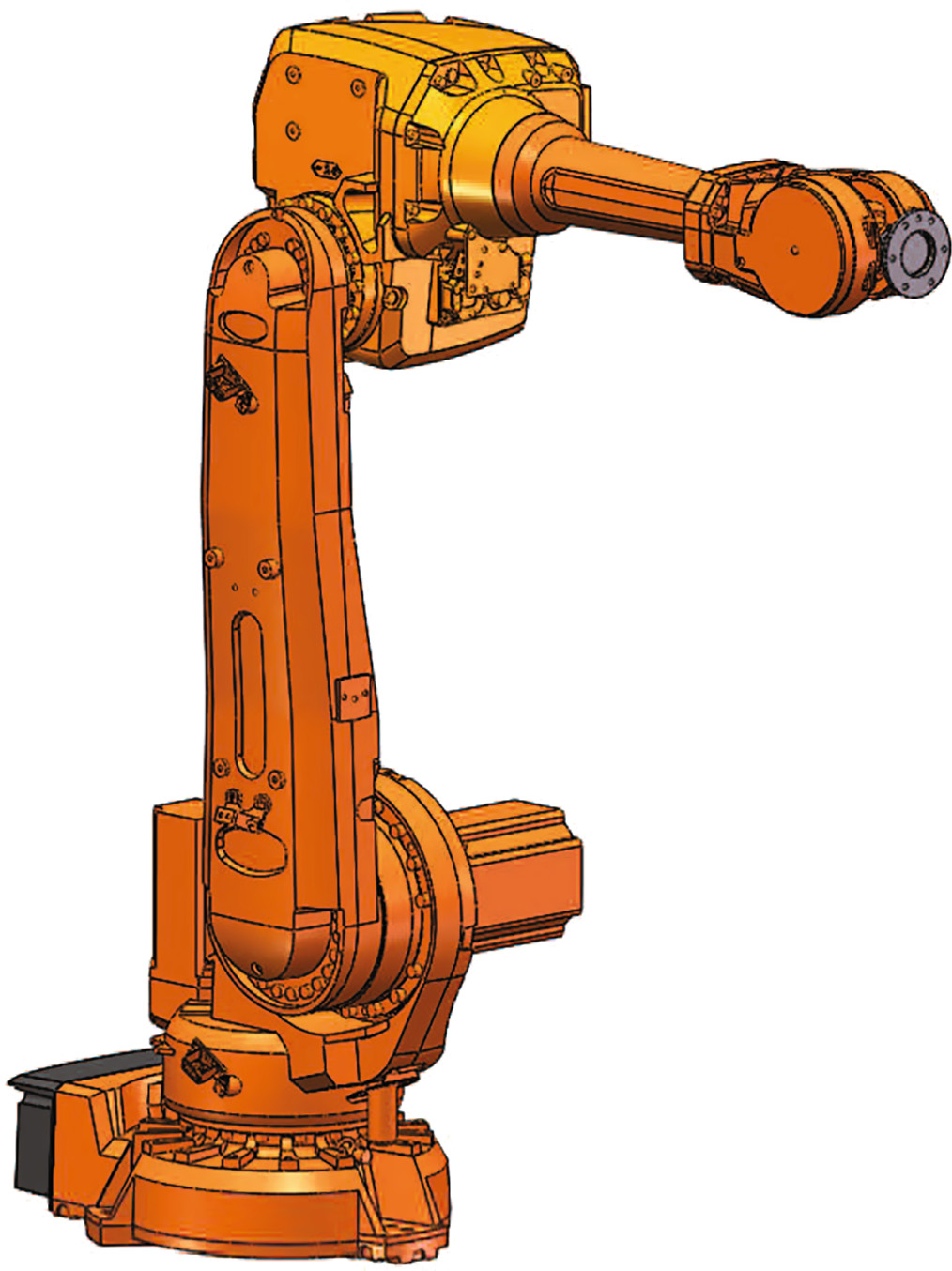
2.1 工业机器人的运动学

根据丹尼维特‐哈滕伯格（D‐H）约定[5],，为机械臂的每个连杆建立笛卡尔坐标系，如图2所示。接下来，令i、j和k分别为沿 x轴、 y轴和 z轴的单位矢量。末端执行器在参考坐标系（x0, y0, z0）中的正向运动学变换矩阵表示为

$$
^0A_6 = \begin{bmatrix} R & q \ 0 & 1 \end{bmatrix} = \prod_{i=1}^{6} {}^{i-1}A_i \quad \text{where} \quad {}^{i-1}A_i = \begin{bmatrix} {}^{i-1}R_i & {}^{i-1}q_i \ 0 & 1 \end{bmatrix}
$$

with
$$
{}^{i-1}R_i = R_{z_{i-1}}(\theta_i)R_{x_i}(\alpha_i) \tag{2a}
$$
$$
{}^{i-1}q_i = [a_i \cos\alpha_i \quad a_i \sin\alpha_i \quad d_i]^T \tag{2b}
$$

其中D‐H参数列于表1中。六轴机器人的逆几何问题在文献中已有充分记载[16]。

关节 i	αi	ai[m]	di[m]	θi
1	π/2	0.175	0.495	θ1
2	0	1.075	0	θ2
3	π/2	0.175	0	θ3
4	−π/2	0	0.960	θ4
5	π/2	0	0	θ5
6	π	0	0.135	θ6

2.2 雅可比矩阵

关节角速度可通过雅可比矩阵按如下方式计算：

$$
\dot{\theta} = J^{-1} \dot{t} \tag{3}
$$

其中 $\dot{\theta}=[\dot{\theta}_1 \dot{\theta}_2… \dot{\theta}_6]^T$ 表示关节角速度向量，而 $\dot{t}=[\omega^T \dot{q}^T]^T$ 代表末端执行器扭速，$\omega$为角速度。此外，J是机械臂的雅可比矩阵[17],，即

$$
J = [j_1 j_2… j_6] \quad \text{where} \quad j_i = \begin{bmatrix} z_{i-1} \ p_{i-1} \times z_{i-1} \end{bmatrix} \tag{4}
$$
with
$$
z_{i-1} = R_{i-1}k; \quad p_{i-1} = q_{i-1} - q \tag{5}
$$

其中 $R_{i-1}$ 和 $q_{i-1}$ 分别表示从参考坐标系到第(i−1)个坐标系的变换矩阵的旋转矩阵和位置向量，它们可从式(1)中的Ai提取。

2.3 机器人动力学

焊接过程中，在负载fe作用下机器人的动态行为可以描述为

$$
M\delta\ddot{t}+ C\delta\dot{t}+ K\delta t= f_e \tag{6}
$$

其中 M是6维质量矩阵，表示机器人在固有频率方面的整体行为，C是6维阻尼矩阵，K是在外部载荷fe[18]作用下机器人的6维笛卡尔刚度矩阵。 $\delta t$、 $\delta\dot{t}$ 和 $\delta\ddot{t}$ 分别是工具端点的瞬时动态位移、速度和加速度。

质量矩阵 M在公式(6)中可根据串联机器人运动动力学方程(EOM)[9]如下求解：

$$
M(\theta)\ddot{\theta}+ v(\theta, \dot{\theta})+ g(\theta)= \tau \tag{7}
$$

其中， $\theta$、 $\dot{\theta}$、 $\ddot{\theta}$ 分别为广义关节角、角速度和角加速度的6维向量。$M(\theta)$ 是 6 × 6一般惯性质量矩阵，$v(\theta, \dot{\theta})$ 是表示科里奥利力和离心力的6维向量，$g(\theta)$ 是考虑重力引起的力的6维向量。此外， $\tau$是作用在关节上的广义外力矢量。

3 柔顺性误差建模与补偿

为了补偿机器人末端执行器的定位误差以实现高质量焊接，需要精确计算由外部有效载荷和机器人自重引起的柔顺性误差，这要求计算机器人的刚度矩阵。

3.1 弹性静力学建模

在本研究中，采用虚拟弹簧法[13]来推导基于螺旋坐标的刚度矩阵[19,20]。图3显示了机械臂的虚拟刚度模型，其中gj, j= 1, 2,…, 8 表示重力，而fe表示外部载荷。

设 $\theta$、 $\theta’$ 分别为关节的原始角位移和变形后的角位移，根据虚功原理，辅助负载所做的功等于内力所做的功 $\tau_\theta$[13]，即

$$
\sum(g_j^T \delta t_j) + f_e^T \delta t = \tau_\theta^T (\theta’ - \theta) \tag{8}
$$

其中，虚位移 $\delta t_j$ 和 $\delta t$ 可根据从 $\delta t_j = J_j(\theta’ - \theta)$ 和 $\delta t = J_\theta(\theta’ - \theta)$ 推导出的线性化几何模型计算得到，Jj 和Jθ 分别为雅可比矩阵，即

$$
J_\theta = [j_1 j_2 J_U j_3 j_4 J_F j_5 j_6] \in \mathbb{R}^{6\times18} \tag{9}
$$
$$
J_j = J_\theta(:, 1: k) \tag{10}
$$

其中Jθ(:, 1: k)表示Jθ的前 k列， k表示从基座到gj的虚拟弹簧的自由度数量。此外，JU和JF分别表示上臂和前臂的连杆变形与末端执行器之间的关系，表达为

$$
J_U = \begin{bmatrix} x_1 \ y_1 \ z_1 \ 0 \ 0 \ 0 \end{bmatrix} \tag{11a}
$$
$$
J_F = \begin{bmatrix} z_3 \ x_3 \ y_3 \ 0 \ 0 \ 0 \end{bmatrix} \tag{11b}
$$

方程（8）被重写为

$$
\sum(g_j^T J_j(\theta’ - \theta)) + f_e^T J_\theta(\theta’ - \theta) = \tau_\theta^T (\theta’ - \theta) \tag{12}
$$

因此，机械臂的力平衡方程推导如下

$$
\tau_\theta = \sum(J^T_G + J_\theta^T F \tag{13})
$$
with
$$
J^T_g = [J_1 J_2… J_8] \in \mathbb{R}^{6\times48}; \quad G = [g_1^T g_2^T … g_8^T]^T \in \mathbb{R}^{48} \tag{14}
$$

根据线性力‐变形关系，平衡条件可写为

$$
J^T_g G + J^T_\theta f_e = K_\theta(\theta’_i - \theta_i) \tag{15}
$$

在关节空间中表示的刚度矩阵Kθ

$$
K_\theta = \text{diag}[K_{act,1} K_{act,2} K_U K_{act,3} K_{act,4} K_F K_{act,5} K_{act,6}] \tag{16}
$$

其中Kact,i为驱动刚度，KU和KF通过欧拉‐伯努利梁模型计算得到，分别表示上臂和前臂的刚度矩阵。

为了计算负载模式的刚度矩阵，假设在负载构型附近，外部载荷和关节位移分别增加一个微小量 $\delta f_e$ 和 $\delta \theta$ 后，仍满足平衡条件，从而得到

$$
(J_g + \delta J_g)^T G + (J_\theta + \delta J_\theta)^T(f_e + \delta f_e) = K_\theta(\theta’ - \theta + \delta \theta) \tag{17}
$$

具有线性化运动学约束：

$$
\delta t = J_\theta \delta \theta \tag{18}
$$

从式(15)中移除不变的平衡条件后，经过线性化，得到式(17)

$$
H^T_g \otimes G \delta \theta + J_\theta^T \delta f_e + H^T_\theta \otimes f_e \delta \theta = K_\theta \delta \theta \tag{19}
$$

其中符号 $\otimes$ 表示矩阵之间的克罗内克积，而$H_g = \partial J_\theta/\partial \theta$，即海森矩阵。联立公式(18)和(19)，工业机器人的运动静力学模型可简化为

$$
\begin{bmatrix} 0 & J_\theta \ \end{bmatrix} \begin{bmatrix} \delta \theta \ \end{bmatrix} = \begin{bmatrix} \delta t \ 0 \end{bmatrix} \tag{20}
$$
with
$$
K_E = H^T_\theta \otimes F \tag{21}
$$

从末端执行器的力‐变形方程 $\delta f_e = K \delta t$，可计算出机器人的笛卡尔刚度矩阵K，

$$
K = (J_\theta(K_\theta - K_E)^{-1} J_\theta^T)^{-1} \tag{22}
$$

3.2 误差补偿程序

工业机器人的运动通常根据逆运动学生成，由此计算出对应于期望的末端执行器位置p的执行器输入信号 $\theta$。然而，当外部载荷$f_e$作用于末端执行器时，由于末端执行器的柔顺性误差 $\delta t$，运动学控制不再适用，因此实际位置需通过刚度模型计算得出。

$$
p’ = p + \delta t \quad \text{where} \quad \delta t = K^{-1} (f_e + J^{-T}\tau) \tag{23}
$$

这里，$f_e + J^{-T}\tau$表示力与惯性力的组合。为了使末端执行器位于期望位置p，应在载荷$f_e$作用下对p与p′之间的compliance误差进行补偿。设

假设在相同的载荷$f_e$作用下，修正后的末端执行器位置为$p_f = p - \delta t$，补偿后的实际位置$p_c$应位于期望位置附近，即

$$
p_c = p_f + \delta t_f \approx p \quad \text{where} \quad \delta t_f = K^{-1}_f(f_e + J^{-T}_f \tau_f) \tag{24}
$$

其中$K_f$是在变形后位置评估的刚度矩阵，$J_f$和$\tau_f$分别是实际位置处的雅可比矩阵和关节力矩。因此，修正后的末端执行器位置$p_f$可通过以下迭代过程计算得出，

$$
p’_c = p + \lambda(p - p_c) \tag{25}
$$

其中带撇项对应于下一次迭代，$\lambda = \Delta t / |p - p_c|$是用于实现收敛的标量参数，$\Delta t$为$p - p_c$中各元素的最大幅值。该迭代方法如图4所示，当 $|p - p_c| \leq \varepsilon$时停止，其中 $\varepsilon$为可接受公差。通过该方法对机器人控制中的参考轨迹进行修正，可补偿柔顺性误差，从而精确跟踪期望轨迹。

4 案例研究中的误差补偿

前述的刚度建模和误差补偿流程以所研究的焊接机器人（即ABB IRB4600）为例进行说明。

机器人，沿图5所示轨迹运动，同时显示了末端执行器的运动曲线。基于有限元分析的评估结果，与表2中所列的驱动刚度相比，上臂和前臂可视为刚性连杆。该机器人的其他详细技术参数和规格可参见用户手册[1]，且作用在机器人末端执行器上的外部力矩假设为纯力$f_e = [200\ -200\ -200]^T$，并视为恒定的。此处对焊接精度的要求高于0.5mm。

Kact,1	Kact,2	Kact,3	Kact,4	Kact,5	Kact,6
0.237	3.32	2.79	0.486	0.521	0.38

(a)
0 20 40 60 80 100 −0.3
−0.25
−0.2
−0.15
−0.1
−0.05
0
0.05
时间 [秒]
end − effector velocity [m/s] vx vy vz

(b)

图6显示了补偿前后定位误差和轨迹的对比。可以看出，当机器人跟踪修正轨迹时，最大定位误差可减小至0.01mm，意味着补偿后的定位误差可以忽略不计，因为它远小于可接受误差。与未补偿时的定位误差相比，机器人精度提高了约98%，使得补偿后的实际轨迹与期望轨迹基本重合，如图6(b)所示。该对比表明，误差补偿方法能有效提高机器人的操作精度，也可应用于其他工业应用，如铣削。

5 结论

本文研究了用于船体焊接的工业机器人的运动静力建模及柔顺性误差补偿。除了考虑驱动与结构刚度外，还结合机械臂重力和焊接中的外部载荷，推导了机器人的笛卡尔刚度矩阵。以及惯性力的影响。引入了一种迭代误差补偿方法，并在焊接轨迹上进行了数值验证。结果表明，该误差补偿流程能够有效提高操作精度，使机械手在可接受的定位误差范围内跟踪期望轨迹。所提出的方法表明，当控制策略基于运动学、动力静力学和动态模型的结合时，可显著提高机械手的精度，该方法也适用于其他工业应用，如加工。