单纯形算法 Simplex Algorithm (二)

为了真正理解单纯形算法的具体步骤，我查阅了许多文章，不过大部分文章会直接叙述单纯形表的操作，对理解算法帮助有限；也有一些文章直接从线性代数上的原理开始叙述，对于非专业人士又太难了。所幸我找到了一个挺不错的在线课程，感觉是我看过叙述单纯形算法最明了直观的资料了，下面的内容主要就是对这个课程的翻译

初始可行解

我们直接就用个例子来叙述算法。还是上一篇的例子：
$$\begin{array}{rl}max& Z=40x_1+50x_2\\ s.t.& x_1+2x_2\le 40\\ & 4x_1+3x_2\le 120\\ & x_1,x_2\ge 0\end{array}$$
把它松弛化：
$$\begin{array}{rl}max& Z=40x_1+50x_2\\ s.t.& x_1+2x_2+s_1=40\\ & 4x_1+3x_2+s_2=120\\ & x_1,x_2,s_1,s_2\ge 0\end{array}$$
在上一篇文章中我是以分块矩阵的形式来表现基变量和非基变量，这里我们有更加直观和简单的方法：把约束方程组中的基变量统一移到等式左侧，非基变量统一移到等式右侧，而目标则通过消元操作用非基变量表示：
$$\begin{array}{rl}max& Z=40x_1+50x_2\\ s.t.& s_1=40-x_1-2x_2\\ & s_2=120-4x_1-3x_2\\ & x_1,x_2,s_1,s_2\ge 0\end{array}$$
然后令非基变量$x_1=x_2=0$，则各个基变量则等于各个约束中的常数项，即$s_1=40,s_2=120$，目标值$Z=0$，我们得到一个初始的可行解
$$\mathbf{x}=\left[\begin{array}{c}{x}_1\\ x_2\\ s_1\\ s_2\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 40\\ 120\end{array}\right]$$

解的转移

有了初始可行解，就可以开始整个算法的迭代过程，每次迭代需要有基变量的出基和非基变量的入基。
首先需要选择一个要变成基变量的非基变量，这里我们必须要选择在约束中系数为负数的变量，在这个例子中，我们可以选择变量$x_1$，它在两个约束等式中的系数都是负数：

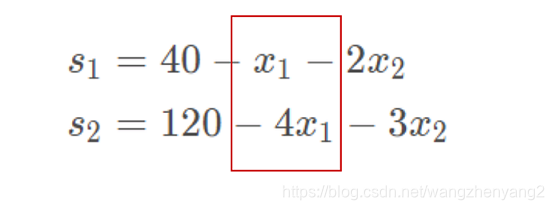
为什么一定要系数为负数? 因为如果是正数，把它移到等式左侧进行规整时等式两边就需要除以一个负数，那么最终约束等式中将存在负数常数项，无法得到可行解。
我们选择了 x 1 x_1 x