Attention is all you need论文解析

《Attention is all you need》论文解析

原创于 2025-08-16 18:22:41 发布 · 1.2k 阅读

11 ·

CC 4.0 BY-SA版权

文章标签：

#语言模型 #人工智能 #自然语言处理 #transformer

《Attention is all you need》这篇论文是谷歌科学家于2027年发表的，是自然语言处理（NLP）和深度学习领域的一篇里程碑式著作。作者在这篇论文中提出了Transformer这个大杀器，它彻底改变了序列建模（尤其是机器翻译）的范式，并催生了后续一系列革命性的大模型（如BERT、GPT系列、T5等）。本文对《Attention is all you need》进行讲解。

在Transformer之前，业界主流的序列模型是基于复杂的循环神经网络或卷积神经网络，然后叠加编码器和解码器。RNN+Seq2Seq比较常见，例如论文《Learning Phrase Representations using RNN Encoder–Decoderfor Statistical Machine Translation》提出了RNN Encoder-Decoder架构，首次将Seq2Seq模型引入到统计机器翻译（SMT）。CNN+Seq2Seq应用于自然语言处理领域可参见论文《Convolutional Sequence to Sequence Learning》。该论文是facebook于2017年提出的，首次成功地将卷积神经网络 (CNN) 应用于序列到序列 (Seq2Seq) 学习任务，并在当时主流的机器翻译基准上取得了极具竞争力甚至超越当时最佳循环神经网络 (RNN/LSTM) 模型的成绩，同时训练速度显著提升。

然而，作者提出的transformer摈弃了RNN和CNN，完全依赖于注意力机制来捕捉输入和输出之间的全局依赖关系。

一、为什么要提出Transformer

1、RNN每次输入一个token，是顺序训练的，无法并行计算；

2、Extended Neural GPU、ByteNet、ConvS2S这些模型都是使用CNN作为基础模块的，它们在关联两个任意输入或输出位置所需的操作数量会随着位置举例的增加而增加，如ConvS2S是线性增加的，ByteNet是对数增加的。这使得学习远距离位置的依赖关系变得更加困难。

因此，Transformer摈弃了RNN和CNN，采用注意力机制。Transformer也是首个完全依赖注意力机制来计算器输入和输出表征的传导模型。

二、Transfomer的模型结构

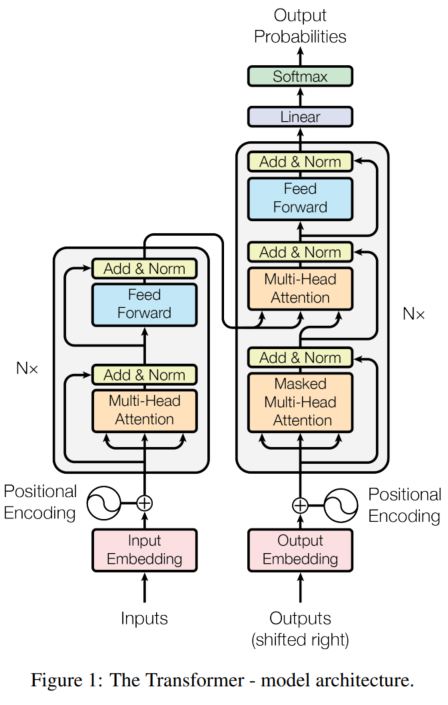
1、如上图所示，Transformer也是采用的Encoder-Decoder架构：

Encoder：上图左侧部分为Encoder，由N=6个完全一样的层组成。每个层由两个子层组成。第一个子层是多头自注意力机制，第二个子层是位置前馈网络 (Position-wise FFN)，即传统的全连接线性变换+非线性激活函数（有两层，第一层将 d_model 维映射到更大的维度 d_ff（如 2048）；应用非线性激活函数（通常是 ReLU 或其变种如 GELU）；第二层将 d_ff 维映射回 d_model 维）。在每个子层中，又叠加了一个残差网络+正则化层。残差网络有助于缓解深层网络中的梯度消失问题，使模型更容易训练深层结构。正则化层在特征维度（d_model 维）上进行归一化，稳定训练并加速收敛。因此，每一子层的输出为 $LayerNorm(x+Sublayer(x))$ ，维度为 $d_{model}=512$ 。
Decoder：上图的右侧部分为Decoder，也是由N=6个完全一样的层组成。从下往上，第一个子层为掩蔽多头自注意力，在训练解码器时，为了确保模型在预测位置 i 的单词时只能依赖位置 1 到 i-1 的已知单词（即之前生成的词），不能“偷看”未来的信息（位置 i 及之后）。这是自回归生成的核心要求。在计算 $Q * K^T$ 得到的相似度矩阵（Attention Scores）后，在应用 softmax 之前，将未来位置对应的分数设置为一个非常大的负数（如 -inf）。这样经过 softmax 后，未来位置的注意力权重就变成了 0。第二子层为多头编码器-解码器注意力，这是连接 Encoder 和 Decoder 的关键桥梁。Query (Q) 来自 Decoder 中前一子层（Masked MHA + Add&Norm）的输出，代表当前解码位置想要查询的信息。Key (K) 和 Value (V) 来自 Encoder Stack 的最终输出 (Memory)，代表源序列的编码信息。第三子层是位置前馈网络 (Position-wise FFN)： 与 Encoder 中的第二子层完全相同。

2、注意力机制和多头自注意力机制

注意力机制和多头注意力机制的详细讲解可参见《注意力机制与自注意力机制》。其中，本论文中的注意力采用“缩放点积注意力机制”，公式为： $Attention(Q,K,V)=softmax(\frac{QK^{T}}{\sqrt{d_{k}}})V$

与点乘注意力机制相比，论文中的注意力机制多了一个缩放因子 $\frac{1}{\sqrt{d_{k}}}$ 。因此叫“缩放点积注意力机制”。公式中的 $d_k$ 为query和key的维度，而value的维度为 $d_{value}$ 。当然，在实际计算中，都是采用矩阵乘法方式进行并行计算。因此，多个query形成了矩阵 $Q$ ，多个key形成了矩阵 $K$ ，多个value形成了矩阵 $V$ 。

在本论文中，作者发现采用多头注意力机制要比单头的效果好（当然，作者也验证了，也不是头越多效果就越好）。多头注意力机制使模型能够同时关注来自不同位置、不同表示子空间的信息。而使用单一注意力头时平均化操作会抑制这种能力。

多头注意力机制的计算公式为： $MultiHead(Q,K,V)=Concat(head_{1},...,head_{h})W^{O}$

其中 $head_{i}=Attention(QW_{i}^{Q},KW_{i}^{K},VW_{i}^{V})$

具体的计算过程可参考《注意力机制十问》。

在该论文中，作者采用了 $h=8$ 个头，每个头的维度为 $d_{k}=d_{v}=d_{model}/h=64$ 。由于每个头的维度都减少了，总的计算开销和采用单头的计算开销差不多。

3、位置前馈网络 (Position-wise FFN)

位置前馈网络的计算公式为： $FFN(x)=max(0,xW_{1}+b_{1})W_{2}+b_{2}$

从公式可以看出来，先进行了线性变换（ $xW_{1}+b_{1}$ ），然后使用了ReLU激活函数，接着又进行了线性变化（ $W_{2}$ 和 $b_{2}$ ）

经过该FFN网络，输入和输出数据的维度变化为 $d_{input}=512\longrightarrow d_{ff}=2028\longrightarrow d_{output}=512$

4、位置编码

由于注意力机制缺失位置信息，因此作者引入了位置编码技术。位置编码是一个与词嵌入 (Word Embedding) 维度相同的向量（维度为 $d_{model}$ ）。对于序列中第 pos 个位置（pos 从 0 开始计数），模型计算出一个特定的位置编码向量 PE(pos)。这个 PE(pos) 向量会直接加到对应位置词的词嵌入向量上。作者所采用的是sine和cosine相对位置编码技术:

$PE_{(pos,2i)}=sin(pos/10000^{2i/d_{model}})$

$PE_{(pos,2i+1)}=cos(pos/10000^{2i/d_{model}})$

上述公式中：

pos：位置（序列中的索引）

i：维度索引，从0到 $d_{model}/2-1$

$d_{model}$ ：词嵌入和位置编码的维度

上述位置编码方式有如下特点：

确定性/固定： 编码是预先计算好的，不是通过训练学习的。模型参数不包含位置编码权重。
泛化性： 理论上可以处理比训练时更长的序列（因为 sin/cos 函数定义域是无限的）。不过实际效果可能下降。
相对位置关系： 一个关键特性是，对于某个固定的偏移量 k，PE(pos + k) 可以表示为 PE(pos) 的线性变换。这使得模型能够相对容易地学习到词之间的相对位置关系（例如，学习一个表示“下一个词”或“前两个词”的向量操作）。
周期性： 不同频率的 sin/cos 波叠加，使得每个位置都有独特的编码模式。

举例说明正弦/余弦位置编码的计算过程：

使用4维向量（ $d_{model}=4$ ，根据计算公式 $i=d_{model}/2-1$ ,可取值为0和1），序列长度为3（计算3个位置：pos=0,1,2）进行举例说明。

（1）对于每个维度索引 $i$ ，计算分母：

i=0:10000^(2*0/4)=10000^0=1
i=1:10000^(2x1/4)=10000^0.5=100

（2）计算位置编码

对于每个位置 $pos$ 和每个 $i$ ，计算正弦（偶数维）和余弦外（奇数维）：

位置0（pos=0）

维度 `i`	计算	维度索引	值
i=0	`sin(0 / 1) = sin(0)`	0（偶）	0.0000
i=0	`cos(0 / 1) = cos(0)`	1（奇）	1.0000
i=1	`sin(0 / 100) = sin(0)`	2（偶）	0.0000
i=1	`cos(0 / 100) = cos(0)`	3（奇）	1.0000

编码向量：[0.0000, 1.0000, 0.0000, 1.0000]

位置 1（pos=1）：

维度 `i`	计算	维度索引	值（保留 4 位小数）
i=0	`sin(1 / 1) = sin(1)`	0（偶）	0.8415
i=0	`cos(1 / 1) = cos(1)`	1（奇）	0.5403
i=1	`sin(1 / 100) = sin(0.01)`	2（偶）	0.0100
i=1	`cos(1 / 100) = cos(0.01)`	3（奇）	0.9999

编码向量：[0.8415, 0.5403, 0.0100, 0.9999]

位置 2（pos=2）：

维度 `i`	计算	维度索引	值（保留 4 位小数）
i=0	`sin(2 / 1) = sin(2)`	0（偶）	0.9093
i=0	`cos(2 / 1) = cos(2)`	1（奇）	-0.4161
i=1	`sin(2 / 100) = sin(0.02)`	2（偶）	0.0200
i=1	`cos(2 / 100) = cos(0.02)`	3（奇）	0.9998