UVA - 11361 Investigating Div-Sum Property 【数位dp】

本文链接：https://blog.youkuaiyun.com/wangws_sb/article/details/83960052

探讨了在给定范围内，寻找既能被特定整数k整除，且其数位和也能被k整除的数的个数的问题。通过动态规划方法，利用加法原理和分段求和技巧，实现了高效求解。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目传送门

题目描述：有t组测试数据(T < 100)，每组测试数据输入三个整数a，b，k，1 ≤ A ≤ B < 2 31 and 0 < K < 10000.求a~b中能够整除k并且数位和也能够整除k的数的个数。

解题思路：设f(x)表示不超过x的非负数中满足条件的数的个数，则本题的答案等于f(b)-f(a-1)。可以考虑用加法原理、分段求和。

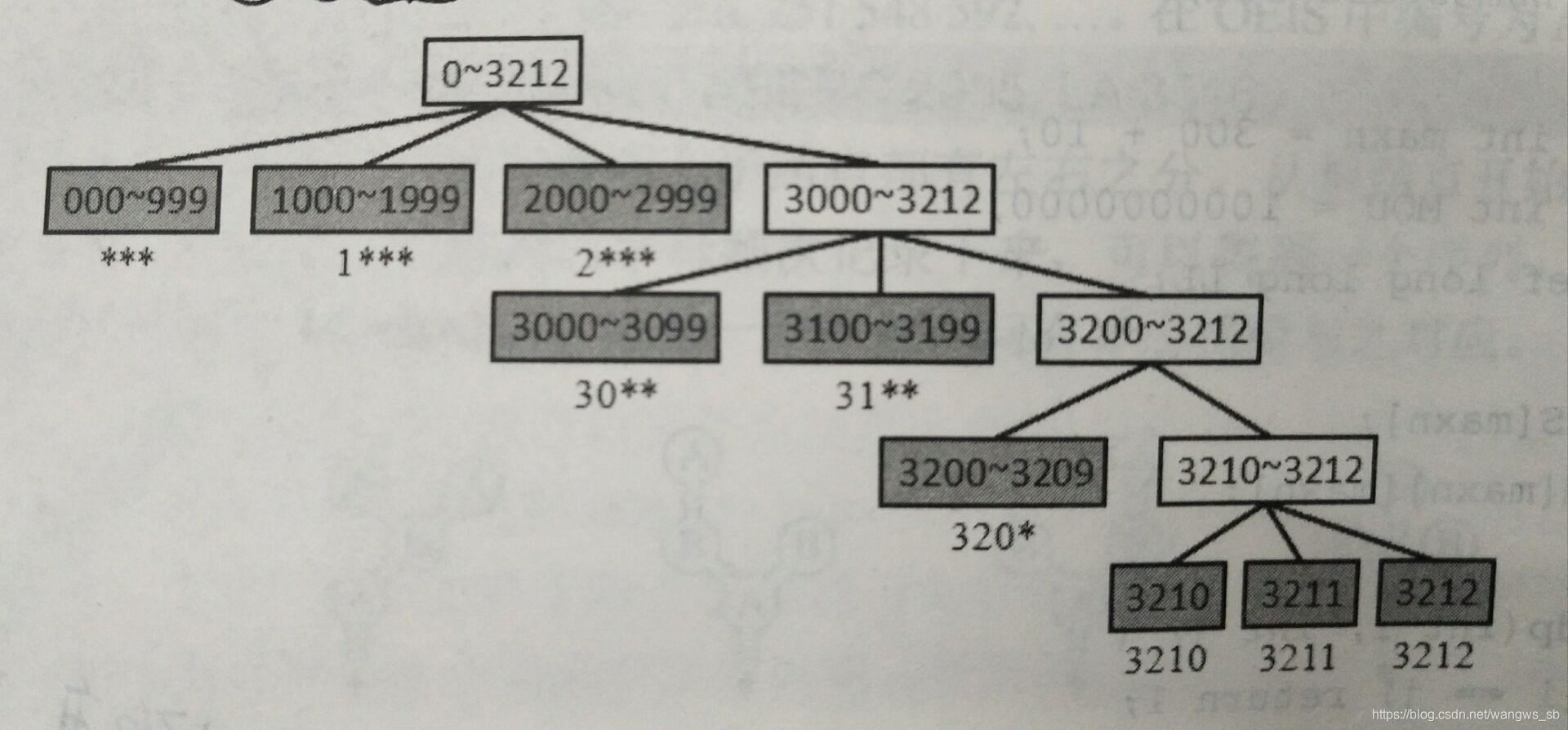
设dp[d][m1][m2]表示共d个数字，其中各数字之和除以k的余数为m1，这些数字组成的整数除以k的余数为m2，则每个模板对应的解的个数都等于某个dp[d][m1][m2]。

递推公式为：f(d,m1,m2)=∑f(d−1,(m1+i)%k,m2+i∗10d−1%k|0⩽i⩽9)

AC代码：

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <queue>
#include <stack>
#include <vector>
#include <map>
#include <set>
using namespace std;
#define io ios::sync_with_stdio(0),cin.tie(0)
#define ms(arr) memset(arr,0,sizeof(arr))
#define inf 0x3f3f3f
typedef long long ll;
const int mod=1e9+7;
const int maxn=1e5+7;
ll t,a,b,k;
int dp[15][120][120];//dp[d][m1][m2]表示共d个数字，其中各数字之和除以k的余数为m1，这些数字组成数位整数除以k的余数为m2的整数的个数
int c[15];
ll dfs(int d,int m1,int m2,bool limit)
{
    if(d==0)
    {
        if(m1==0&&m2==0)
            return 1;
        else
            return 0;
    }
    if(!limit&&dp[d][m1][m2]>=0)
        return dp[d][m1][m2];
    int up;//up存的是当前数位的上界
    if(limit)//limit表示前一数位是否达到上界
        up=c[d];
    else
        up=9;
    ll ans=0;
    for(int i=0;i<=up;i++)
    {
        ans+=dfs(d-1,(m1+i)%k,(m2*10+i)%k,limit&&(i==up));
    }
    dp[d][m1][m2]=ans;
    return dp[d][m1][m2];
}
ll f(int x)
{
    int cnt=0;
    while(x)
    {
        c[++cnt]=x%10;
        x=x/10;
    }
    memset(dp,-1,sizeof(dp));
    return dfs(cnt,0,0,1);
}
int main()
{
    cin>>t;
    while(t--)
    {
        cin>>a>>b>>k;
        ll ans;
        if(k>=83)
            ans=0;
        else
            ans=f(b)-f(a-1);
        cout<<ans<<endl;
    }
    return 0;
}