数据结构--搜索BFS

广度优先搜索

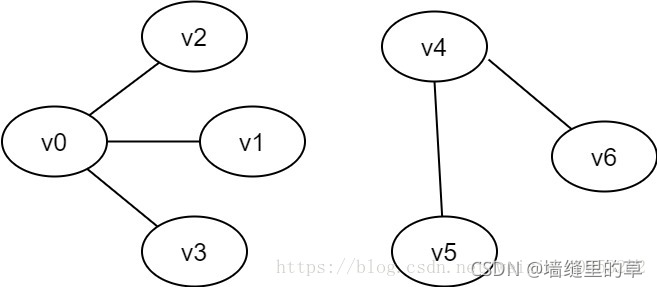
广度优先搜索类似于树的层次遍历过程。它需要借助一个队列来实现。如图2-1-1所示，要想遍历从v0到v6的每一个顶点，我们可以设v0为第一层，v1、v2、v3为第二层，v4、v5为第三层，v6为第四层，再逐个遍历每一层的每个顶点。

BFS算法一般应用于单源最短路径的搜索。

1、寻找非加权图（或者所有边权重相同）中任两点的最短路径。

2、寻找其中一个连通分支中的所有节点。（扩散性）
3、bfs染色法判断是否为二分图。

#include<iostream>
#include<queue>
#include<string.h>
#define maxn 105
using namespace std;
 
int n,m;    //矩阵的大小 
int sx,sy; 
int vis[maxn][maxn],s[maxn][maxn],t[maxn][maxn];
queue<struct node>Q; 
int px[]={1,-1,0,0};        //人可走的4个方向 
int py[]={0,0,1,-1};
struct node{
    int x,y,step;
}r,p,q;
 
int BFS()
{   
    //清空队列及初始化vis数组 
    while(!Q.empty())
        Q.pop();
    memset(vis,0,sizeof(vis));
    p.x=sx;
    p.y=sy;
    p.step=0;
    vis[p.x][p.y]=1;
    Q.push(p);
    while(!Q.empty())
    {
        p=Q.front();
        Q.pop();
        if(s[p.x][p.y]=='t')
            return p.step;
        for(int i=0;i<4;i++)
        {
            q=p;
            q.x+=px[i];
            q.y+=py[i];
            q.step++;
            if(q.x<0||q.y<0||q.x>=n||q.y>=m)
                continue;
            //访问未被访问过的位置，且此时是在火势蔓延到此前访问的，再将该位置入队
            if(vis[q.x][q.y]==0&&q.step<t[q.x][q.y])
            {
                vis[q.x][q.y]=1;
                Q.push(q);
            }
        }
    }
    return -1;
}
 

典型例题

走迷宫问题
给定一个 n×m 的二维整数数组，用来表示一个迷宫，数组中只包含 0 或 1，其中 0 表示可以走的路，1 表示不可通过的墙壁。

最初，有一个人位于左上角 (1,1) 处，已知该人每次可以向上、下、左、右任意一个方向移动一个位置。

请问，该人从左上角移动至右下角 (n,m) 处，至少需要移动多少次。

数据保证 (1,1) 处和 (n,m) 处的数字为 0，且一定至少存在一条通路。

#include<iostream>
#include<cstring>
using namespace std;

const int N=110;
int g[N][N],d[N][N];
int n,m;
struct elem{
    int x;
    int y;
};
struct elem q[N*N];


int bfs(){
    int hh=0,tt=0;
    memset(d,-1,sizeof(d));
    d[0][0]=0;
   //struct elem j=q[hh++];
    int dx[4]={1,0,-1,0};
    int dy[4]={0,1,0,-1};
    while(hh<=tt){
        struct elem j=q[hh++];
        for(int i=0;i<4;i++){
            int x=j.x+dx[i];
            int y=j.y+dy[i];
            if(x>=0&&y>=0&&x<n&&y<m&&g[x][y]==0&&d[x][y]==-1){
            
            d[x][y]=d[j.x][j.y]+1;
            q[++tt]={x,y};
        }}
    }
    return d[n-1][m-1];
}
int main(){
    cin>>n>>m;
    for(int i=0;i<n;i++)
    for(int j=0;j<m;j++)
    cin>>g[i][j];
    cout<<bfs()<<endl;
    return 0;
}

在走迷宫问题中BFS是可以找到最短路径的并且可以同时找到某点到其他任意点的最短路径，但DFS只能是找到其中一条成立的路径

在例题：八数码（类似华容道）问题上也可以找到最少交换次数

#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <queue>

using namespace std;

int bfs(string state)
{
    queue<string> q;
    unordered_map<string, int> d;

    q.push(state);
    d[state] = 0;

    int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};

    string end = "12345678x";
    while (q.size())
    {
        auto t = q.front();
        q.pop();

        if (t == end) return d[t];

        int distance = d[t];
        int k = t.find('x');
        int x = k / 3, y = k % 3;
        for (int i = 0; i < 4; i ++ )
        {
            int a = x + dx[i], b = y + dy[i];
            if (a >= 0 && a < 3 && b >= 0 && b < 3)
            {
                swap(t[a * 3 + b], t[k]);
                if (!d.count(t))
                {
                    d[t] = distance + 1;
                    q.push(t);
                }
                swap(t[a * 3 + b], t[k]);
            }
        }
    }

    return -1;
}

int main()
{
    char s[2];

    string state;
    for (int i = 0; i < 9; i ++ )
    {
        cin >> s;
        state += *s;
    }

    cout << bfs(state) << endl;

    return 0;
}