1.11 LeetCode总结（基本算法）_回溯

原创已于 2025-09-27 11:30:38 修改 · 239 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #leetcode #职场和发展

于 2020-11-28 00:17:11 首次发布

日刻一诗专栏收录该内容

30 篇文章

订阅专栏

本文精选了若干经典算法题目，包括全排列、有效数独、括号生成等，并提供了详细的解题思路及代码实现，旨在帮助读者理解并掌握算法设计与实现的方法。

编程总结

每每刷完一道题后，其思想和精妙之处没有地方记录，本篇博客用以记录刷题过程中的遇到的算法和技巧

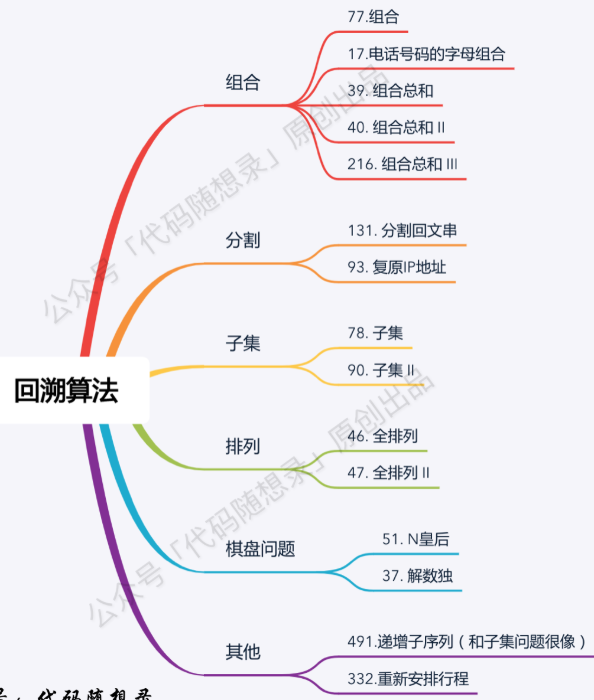
回溯法，一般可以解决如下几种问题：

组合问题：N个数里面按一定规则找出k个数的集合
切割问题：一个字符串按一定规则有几种切割方式
子集问题：一个N个数的集合里有多少符合条件的子集
排列问题：N个数按一定规则全排列，有几种排列方式
棋盘问题：N皇后，解数独等等

一、组合

77. 组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按任何顺序返回答案。
示例 1：
输入：n = 4, k = 2
输出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
示例 2：
输入：n = 1, k = 1
输出：[[1]]
提示：
1 <= n <= 20
1 <= k <= n

int *path;
int pathTop;
int **ans;
int ansTop;
void backtracking(int n, int k, int startIndex)
{
    // 当path中元素个数为k个时，我们需要将path数组放入ans二维数组中
    if (pathTop == k) {
        // path数组为我们动态申请，若直接将其地址放入二维数组，path数组中的值会随着我们回溯而逐渐变化
        // 因此创建新的数组存储path中的值
        int *temp = (int *)malloc(sizeof(int) * k);
        for (int i = 0; i < k; i++) {
            temp[i] = path[i];
        }
        ans[ansTop++] = temp;
        return;
    }
    for (int j = startIndex; j <= n - (k - pathTop) + 1;j++) {
        //将当前结点放入path数组
        path[pathTop++] = j;
        //进行递归
        backtracking(n, k, j + 1);
        //进行回溯，将数组最上层结点弹出
        pathTop--;
    }
}
int **combine(int n, int k, int *returnSize, int **returnColumnSizes)
{
    //path数组存储符合条件的结果
    path = (int *)malloc(sizeof(int) * k);
    //ans二维数组存储符合条件的结果数组的集合。（数组足够大，避免极端情况）
    ans = (int **)malloc(sizeof(int *) * 10000);
    pathTop = ansTop = 0;
    //回溯算法
    backtracking(n, k, 1);
    //最后的返回大小为ans数组大小
    *returnSize = ansTop;
    //returnColumnSizes数组存储ans二维数组对应下标中一维数组的长度（都为k）
    *returnColumnSizes = (int *)malloc(sizeof(int) * (*returnSize));
    for (int i = 0; i < *returnSize; i++) {
        (*returnColumnSizes)[i] = k;
    }
    //返回ans二维数组
    return ans;
}

17.电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按任意顺序返回。
给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。
在这里插入图片描述
示例 1：
输入：digits = “23”
输出：[“ad”,“ae”,“af”,“bd”,“be”,“bf”,“cd”,“ce”,“cf”]
示例 2：
输入：digits = “”
输出：[]
示例 3：
输入：digits = “2”
输出：[“a”,“b”,“c”]
提示：
0 <= digits.length <= 4
digits[i] 是范围 [‘2’, ‘9’] 的一个数字。

char *path;
int pathTop;
char **result;
int resultTop;
char *letterMap[10] = { "", //0
        "", //1
        "abc", //2
        "def", //3
        "ghi", //4
        "jkl", //5
        "mno", //6
        "pqrs", //7
        "tuv", //8
        "wxyz", //9
};
void backTracking(char *digits, int index)
{
    // 若当前下标等于digits数组长度
    if (index == strlen(digits)) {
        //复制digits数组，因为最后要多存储一个0，所以数组长度要+1
        char *tempString = (char *)malloc(sizeof(char) * strlen(digits) + 1);
        for (int j = 0; j < strlen(digits); j++) {
            tempString[j] = path[j];
        }
        //char数组最后要以0结尾
        tempString[strlen(digits)] = 0;
        result[resultTop++] = tempString;
        return;
    }
    //将字符数字转换为真的数字
    int digit = digits[index] - '0';
    //找到letterMap中对应的字符串
    char *letters = letterMap[digit];
    for (int i = 0; i < strlen(letters); i++) {
        path[pathTop++] = letters[i];
        //递归，处理下一层数字
        backTracking(digits, index + 1);
        pathTop--;
    }
}
char **letterCombinations(char *digits, int *returnSize)
{
    //初始化path和result
    path = (char *)malloc(sizeof(char) * strlen(digits));
    result = (char **)malloc(sizeof(char*) * 300);
    *returnSize = 0;
    //若digits数组中元素个数为0，返回空集
    if (strlen(digits) == 0) {
        return result;
    }
    pathTop = 0;
    resultTop = 0;
    backTracking(digits, 0);
    *returnSize = resultTop;
    return result;
}

39. 组合总和

给你一个无重复元素的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的所有不同组合，并以列表形式返回。你可以按任意顺序返回这些组合。
candidates 中的同一个数字可以无限制重复被选取。如果至少一个数字的被选数量不同，则两种组合是不同的。
对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：
输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

示例 2：
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：
输入: candidates = [2], target = 1
输出: []

提示：
1 <= candidates.length <= 30
2 <= candidates[i] <= 40
candidates 的所有元素互不相同
1 <= target <= 40

131. 分割回文串

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是回文串。返回 s 所有可能的分割方案。
示例 1：
输入：s = “aab”
输出：[[“a”,“a”,“b”],[“aa”,“b”]]
示例 2：
输入：s = “a”
输出：[[“a”]]
提示：
1 <= s.length <= 16
s 仅由小写英文字母组成

char **path;
int pathTop;
char ***ans;
int ansTop = 0;
int *ansSize;
//将path中的字符串全部复制到ans中
void copy()
{
    //创建一个临时tempPath保存path中的字符串
    char **tempPath = (char **)malloc(sizeof(char *) * pathTop);
    for (int i = 0; i < pathTop; i++) {
        tempPath[i] = path[i];
    }
    //保存tempPath
    ans[ansTop] = tempPath;
    //将当前path的长度（pathTop）保存在ansSize中
    ansSize[ansTop++] = pathTop;
}
//判断字符串是否为回文字符串
bool isPalindrome(char *str, int startIndex, int endIndex)
{
    //双指针法：当endIndex（右指针）的值比startIndex（左指针）大时进行遍历
    while (endIndex >= startIndex) {
        //若左指针和右指针指向元素不一样，返回False
        if (str[endIndex--] != str[startIndex++]) {
            return 0;
        }
    }
    return 1;
}
//切割从startIndex到endIndex子字符串
char *cutString(char *str, int startIndex, int endIndex)
{
    //开辟字符串的空间
    char *tempString = (char *)malloc(sizeof(char) * (endIndex - startIndex + 2));
    int index = 0;
    //复制子字符串
    for (int i = startIndex; i <= endIndex; i++) {
        tempString[index++] = str[i];
    }
    //用'\0'作为字符串结尾
    tempString[index] = '\0';
    return tempString;
}
void backTracking(char *str, int strLen, int startIndex)
{
    if (startIndex >= strLen) {
        //将path拷贝到ans中
        copy();
        return;
    }
    for (int i = startIndex; i < strLen; i++) {
        //若从subString到i的子串是回文字符串，将其放入path中
        if (isPalindrome(str, startIndex, i)) {
            path[pathTop++] = cutString(str, startIndex, i);
        }
        //若从startIndex到i的子串不为回文字符串，跳过这一层 
        else {
            continue;
        }
        //递归判断下一层
        backTracking(str, strLen, i + 1);
        //回溯，将path中最后一位元素弹出
        pathTop--;
    }
}
char*** partition(char *s, int *returnSize, int **returnColumnSizes)
{
    int strLen = strlen(s);
    //因为path中的字符串最多为strLen个（即单个字符的回文字符串），所以开辟strLen个char*空间
    path = (char **)malloc(sizeof(char *) * strLen);
    //存放path中的数组结果
    ans = (char ***)malloc(sizeof(char **) * 40000);
    //存放ans数组中每一个char**数组的长度
    ansSize = (int *)malloc(sizeof(int) * 40000);
    ansTop = pathTop = 0;
    //回溯函数
    backTracking(s, strLen, 0);
    //将ansTop设置为ans数组的长度
    *returnSize = ansTop;
    //设置ans数组中每一个数组的长度
    *returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
    for (int i = 0; i < ansTop; ++i) {
        (*returnColumnSizes)[i] = ansSize[i];
    }
    return ans;
}

93. 复原IP地址

给定一个只包含数字的字符串，复原它并返回所有可能的 IP 地址格式。
有效的 IP 地址正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 ‘.’ 分隔。
例如：“0.1.2.201” 和 “192.168.1.1” 是有效的 IP 地址，但是 “0.011.255.245”、“192.168.1.312” 和 “192.168@1.1” 是无效的 IP 地址。

示例 1：
输入：s = “25525511135”
输出：[“255.255.11.135”,“255.255.111.35”]
示例 2：
输入：s = “0000”
输出：[“0.0.0.0”]
示例 3：
输入：s = “1111”
输出：[“1.1.1.1”]
示例 4：
输入：s = “010010”
输出：[“0.10.0.10”,“0.100.1.0”]
示例 5：
输入：s = “101023”
输出：[“1.0.10.23”,“1.0.102.3”,“10.1.0.23”,“10.10.2.3”,“101.0.2.3”]
提示：
0 <= s.length <= 3000
s 仅由数字组成

//记录结果
char **result;
int resultTop;
//记录应该加入'.'的位置
int segments[3];
int isValid(char *s, int start, int end)
{
    if (start > end) {
        return 0;
    }
    if (s[start] == '0' && start != end) { // 0开头的数字不合法
        return false;
    }
    int num = 0;
    for (int i = start; i <= end; i++) {
        if (s[i] > '9' || s[i] < '0') { // 遇到非数字字符不合法
            return false;
        }
        num = num * 10 + (s[i] - '0');
        if (num > 255) { // 如果大于255了不合法
            return false;
        }
    }
    return true;
}
//startIndex为起始搜索位置，pointNum为'.'对象
void backTracking(char *s, int startIndex, int pointNum)
{
    //若'.'数量为3，分隔结束
    if (pointNum == 3) {
        //若最后一段字符串符合要求，将当前的字符串放入result种
        if (isValid(s, startIndex, strlen(s) - 1)) {
            char *tempString = (char *)malloc(sizeof(char) * strlen(s) + 4);
            //记录添加字符时tempString的下标
            int count = 0;
            //记录添加字符时'.'的使用数量
            int count1 = 0;
            for (int j = 0; j < strlen(s); j++) {
                tempString[count++] = s[j];
                //若'.'的使用数量小于3且当前下标等于'.'下标，添加'.'到数组
                if (count1 < 3 && j == segments[count1]) {
                    tempString[count++] = '.';
                    count1++;
                }
            }
            tempString[count] = 0;
            //扩容result数组
            result = (char **)realloc(result, sizeof(char *) * (resultTop + 1));
            result[resultTop++] = tempString;
        }
        return;
    }
    for (int i = startIndex; i < strlen(s); i++) {
        if (isValid(s, startIndex, i)) {
            //记录应该添加'.'的位置
            segments[pointNum] = i;
            backTracking(s, i + 1, pointNum + 1);
        } else {
            break;
        }
    }
}
char **restoreIpAddresses(char *s, int *returnSize)
{
    result = (char **)malloc(0);
    resultTop = 0;
    backTracking(s, 0, 0);
    *returnSize = resultTop;
    return result;
}

全排列

46. 全排列

给定一个不含重复数字的数组 nums ，返回其所有可能的全排列。你可以按任意顺序返回答案。
在这里插入图片描述

复用DFS的思路，找递归终止条件等思路一致
在找到满足条件的数组时，拷贝数组的手法值得学习

 /* 定义当前遍历深度count为全局变量 */
int gCount;
void DFS(int *nums, int numsSize, int depth, int *path, int *visited, int **res)
{
	// 递归终止条件，满足 depth == numSize
	if (depth == numsSize) {
		res[gCount] = (int *)malloc(sizeof(int) * numsSize);
		memcpy(res[gCount++], path, sizeof(int) * numsSize);
		return;
	}
	for (int i = 0; i < numsSize; i++) {
		// 如果已经遍历了，continue
		if (visited[i] == 1) {
			continue;
		}
		path[depth] = nums[i];
		visited[i] = 1;
		DFS(nums, numsSize, depth + 1, path, visited, res);
		visited[i] = 0;
	}
}
int **permute(int *nums, int numsSize, int *returnSize, int **returnColumnSizes) 
{
	(*returnSize) = 1; // 初始值
	gCount = 0;
	// 排列数 n!
	for (int i = 1; i <= numsSize; i++) {
		(*returnSize) *= i;
	}
	*returnColumnSizes = (int *)malloc(sizeof(int) * (*returnSize));
	for (int i = 0; i < (*returnSize); i++) {
		(*returnColumnSizes)[i] = numsSize;
	}
	int **res = (int **)malloc(sizeof(int *) * (*returnSize));
	int *path = (int *)malloc(sizeof(int) * numsSize);
	int *visited = (int *)malloc(numsSize * sizeof(int));
	DFS(nums, numsSize, 0, path, visited, res);
	return res;
}

36. 有效的数独

在这里插入图片描述
TBD 使用HASHMAP？

22.括号生成

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且有效的括号组合。
在这里插入图片描述

回溯算法递归求解：
如果左括号数量不大于 n，我们可以放一个左括号。
如果右括号数量小于左括号的数量，我们可以放一个右括号。

在这里插入图片描述

#define MAX_SIZE  1430 // MAX_SIZE 应是一个卡特兰数，官方测试用例中 n 最多为 8，所以 MAX_SIZE = 1430 即可
void dfs(int left, int right, int n, char *str, int index, char **result, int *returnSize) 
{
  // 左右括号都用完
  if (left == n && right == n) {
    result[(*returnSize)] =  (char *)malloc((2 * n + 1)*sizeof(char));
    str[index] = '\0';
	strcpy(result[(*returnSize)++], str);
    return;
  }
  // 当左括号没用完时
  if (left < n) {
    str[index] = '(';
    dfs(left + 1, right, n, str, index + 1, result, returnSize);
  }
  // 右括号数量必须小于左括号，否则一定不合法，且右括号没有用完
  if (left > right && right < n) {
    str[index] = ')';
    dfs(left, right + 1, n, str, index + 1, result, returnSize);
  }
}
char **generateParenthesis(int n, int *returnSize) 
{
  char *str = (char*)malloc((2 * n + 1)*sizeof(char));
  char **result = (char **)malloc(sizeof(char *)*MAX_SIZE);
  *returnSize = 0;
  dfs(0, 0, n, str, 0, result, returnSize);
  return result;
}

448. 找到所有数组中消失的数字

给定一个范围在 1 ≤ a[i] ≤ n ( n = 数组大小 ) 的整型数组，数组中的元素一些出现了两次，另一些只出现一次。
找到所有在 [1, n] 范围之间没有出现在数组中的数字。
您能在不使用额外空间且时间复杂度为O(n)的情况下完成这个任务吗? 你可以假定返回的数组不算在额外空间内。

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
//原地哈希
int* findDisappearedNumbers(int* nums, int numsSize, int* returnSize)
{
    for (int i = 0; i < numsSize; i++) {
        if (nums[labs(nums[i])-1]>0) {
            nums[labs(nums[i])-1]*=-1;
        }
    }
    int *ret = (int *)malloc(sizeof(int )*numsSize);
    
    *returnSize=0;

    for (int i=0; i < numsSize; i++) {
        if (nums[i] > 0){
            ret[*returnSize]=i+1;
            (*returnSize)++;
        }
    }
    
    return ret;
}

遍历输入数组的每个元素一次。
我们将把 |nums[i]|-1 索引位置的元素标记为负数。即 nums[|nums[i] |- 1] \times -1nums[∣nums[i]∣−1]×−1 。
然后遍历数组，若当前数组元素 nums[i] 为负数，说明我们在数组中存在数字 i+1。

39. 组合总和

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明：
所有数字（包括 target）都是正整数。
解集不能包含重复的组合。
在这里插入图片描述

int candidatesSize_tmp;
int ansSize;
int combineSize;
int* ansColumnSize;

void dfs(int* candidates, int target, int** ans, int* combine, int idx) {
    if (idx == candidatesSize_tmp) {
        return;
    }
    if (target == 0) {
        int* tmp = malloc(sizeof(int) * combineSize);
        for (int i = 0; i < combineSize; ++i) {
            tmp[i] = combine[i];
        }
        ans[ansSize] = tmp;
        ansColumnSize[ansSize++] = combineSize;
        return;
    }
    // 直接跳过
    dfs(candidates, target, ans, combine, idx + 1);
    // 选择当前数
    if (target - candidates[idx] >= 0) {
        combine[combineSize++] = candidates[idx];
        dfs(candidates, target - candidates[idx], ans, combine, idx);
        combineSize--;
    }
}

int** combinationSum(int* candidates, int candidatesSize, int target, int* returnSize, int** returnColumnSizes) {
    candidatesSize_tmp = candidatesSize;
    ansSize = combineSize = 0;
    int** ans = malloc(sizeof(int*) * 1001);
    ansColumnSize = malloc(sizeof(int) * 1001);
    int combine[2001];
    dfs(candidates, target, ans, combine, 0);
    *returnSize = ansSize;
    *returnColumnSizes = ansColumnSize;
    return ans;
}

93. 复原 IP 地址

有效 IP 地址正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 ‘.’ 分隔。
例如：“0.1.2.201” 和 “192.168.1.1” 是有效 IP 地址，但是 “0.011.255.245”、“192.168.1.312” 和 “192.168@1.1” 是无效 IP 地址。
给定一个只包含数字的字符串 s ，用以表示一个 IP 地址，返回所有可能的有效 IP 地址，这些地址可以通过在 s 中插入 ‘.’ 来形成。你不能重新排序或删除 s 中的任何数字。你可以按任何顺序返回答案。

示例 1：
输入：s = “25525511135”
输出：[“255.255.11.135”,“255.255.111.35”]
示例 2：
输入：s = “0000”
输出：[“0.0.0.0”]
示例 3：
输入：s = “101023”
输出：[“1.0.10.23”,“1.0.102.3”,“10.1.0.23”,“10.10.2.3”,“101.0.2.3”]
提示：
1 <= s.length <= 20
s 仅由数字组成

int  segments[4];
int  idx;
char **ans;
void dfs(char *s, int segId, int segStart)
{
	int len_s = strlen(s);
	if (segId == 4) {
		if (segStart == len_s) {
			// 如果找到了 4 段 IP 地址并且遍历完了字符串，那么就是一种答案
			char *ipAddr = (char *)malloc(sizeof(char) * (len_s + 4));
			int addr = 0;
			for (int i = 0; i < 4; ++i) {
				int number = segments[i];
				if (number >= 100) {
					ipAddr[addr++] = number / 100 + '0';
				}
				if (number >= 10) {
					ipAddr[addr++] = number % 100 / 10 + '0';
				}
				ipAddr[addr++] = number % 10 + '0';
				if (i != 4 - 1) {
					ipAddr[addr++] = '.';
				}
			}
			ipAddr[addr] = 0;
			ans[idx] = (char *)malloc(sizeof(char) * (len_s + 4));
			ans[idx] = ipAddr;
			idx = idx + 1;
		}
		return;
	}
	// 如果还没有找到 4 段 IP 地址就已经遍历完了字符串，那么提前回溯
	if (segStart == len_s) {
		return;
	}
	// 由于不能有前导零，如果当前数字为 0，那么这一段 IP 地址只能为 0
	if (s[segStart] == '0') {
		segments[segId] = 0;
		dfs(s, segId + 1, segStart + 1);
		return;
	}
	// 一般情况，枚举每一种可能性并递归
	int addr = 0;
	for (int segEnd = segStart; segEnd < len_s; ++segEnd) {
		addr = addr * 10 + (s[segEnd] - '0');
		if ((addr > 0) && (addr <= 0xFF)) {
			segments[segId] = addr;
			dfs(s, segId + 1, segEnd + 1);
		}
		else {
			break;
		}
	}
}
char **restoreIpAddresses(char *s, int *returnSize)
{
	ans = (char **)malloc(sizeof(char *) * 21);
	idx = 0;
	dfs(s, 0, 0);
	(*returnSize) = idx;
	return ans;
}
int main(void)
{
	char str[101] = { "25525511135" };
	int returnSize = 0;
	restoreIpAddresses(str, &returnSize);
	for (int i = 0; i < returnSize; i++) {
		printf("%s\n", ans[i]);
	}
	return 0;
}