c++经典排序算法

最新推荐文章于 2025-04-14 22:26:17 发布

活在自己世界中

最新推荐文章于 2025-04-14 22:26:17 发布

阅读量173

点赞数

文章标签： c++

本文链接：https://blog.youkuaiyun.com/wangwangchang/article/details/118927389

版权

c++各种经典排序算法

从今天开始，写一下找工作所学的内容。

一、各种排序 算法的时间空间复杂度、稳定性⭐⭐⭐⭐⭐

二、（各种排序 算法什么时候有最好情况、最坏情况（尤其是快排））

三、冒泡排序⭐⭐⭐⭐

// 冒泡排序 相邻2个元素 相互比较，直到最后 然后重新开始。
void BubbleSort(int a[], int len) {
    int tmp;
    int exchange = 1;
    for (int i = 0; (i < len - 1) && (exchange > 0); i++) {
        exchange = 0;
        for (int j = 0; j < len - 1 - i; j++) {
            if (a[j] > a[j + 1]) {
                tmp = a[j];
                a[j] = a[j + 1];
                a[j + 1] = tmp;
                exchange = 1;
            }
        }
    }
}

最佳的时候：时间复杂度O(n) 。元素本来有序排列

最坏的时候：时间复杂度O( $n^2$ ) 。数据元素是逆序的

一般情况：时间复杂度O( $n^2$ )。

稳定性：每次比较的时候如果相邻的两个元素想等，不交换顺序。

空间复杂度：O(1)

四、插入排序⭐⭐⭐⭐

//插入排序
//拿出一个数和前面的数进行比较，遇到不比它大的数字，插入其中
void InsertSort(int a[],int len) {
    int tmp;
    for (int i = 0; i < len; i++) {
        tmp = a[i];
        int  k = i; // 记录插入的位置
        for (int j = i-1; (j >= 0) && (a[j] > tmp); j--) {
            a[j + 1] = a[j];
            k = j;
        }
        a[k] = tmp;
    }
}

最佳情况：时间复杂度O(n) 整个序列已经排序第一个元素比较0次，第二个元素比较1次，第n个元素比较1次。

最坏情况：时间复杂度O( $n^2$ ) 整个序列逆序

平均时间复杂度：O( $n^2$ )

稳定性：稳定

空间复杂度：O(1)

五、希尔排序⭐⭐⭐⭐

首先将大数据集分为几个小数据集，然后向每个小数据集进行插入排序。

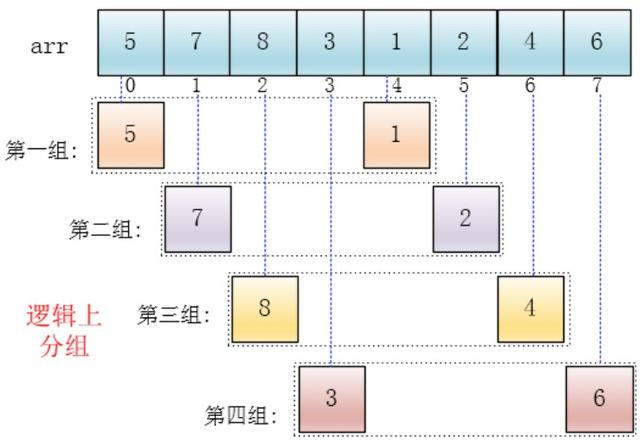
初始增量gap=length/2, 此例是按下标相隔距离为4分的组，也就是说把下标相差4的分到一组，比如这个例子中a[0]与a[4]是一组、a[1]与a[5]是一组…

插入排序完成后

缩小增量为上个增量的一半: gap =4/2，继续划分分组，此时，每个分组元素个数多了，但是，数组变的部分有序了，插入排序效率同样比高。

设置增量为上一个增量的一半：gap=2/2`，则整个数组被分为一组组，此时，整个数组已经接近有序了，插入排序效率高。

//希尔排序
//解决 最大值在第一位 需要移动n-1个位置
void  ShellSort(int a[], int n) {
    int gap = n;
    int tmp;
    while (gap > 1) {
        gap = gap / 3 + 1;
        for (int i = gap; i < n; i += gap) {
            int k = i;
            tmp = a[i];
            for (int j = i -gap; (j >= 0) && (a[j] > tmp); j -= gap) {
                a[j + 1] = a[j];
                k = j;
            }
            a[k] = tmp;
        }
    }
}

最佳情况: T(n) = O(nlog2 n) 已排好序的情况
最坏情况: T(n) = O(nlog_2 n)
平均情况: T(n) =O(nlog2n)
稳定性: 不稳定。虽然插入排序是稳定的，但是希尔排序在插入的时候可能是跳跃性的，所以不是稳定的，可能会破坏稳定性

六、归并排序⭐⭐⭐⭐

即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表。
把长度为n的输入序列分成两个长度为n/2的子序列；对这两个子序列分别采用归并排序；将两个排序好的子序列合并成一个最终的排序序列。

//归并排序
//即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表。
//把长度为n的输入序列分成两个长度为n/2的子序列；对这两个子序列分别采用归并排序；将两个排序好的子序列合并成一个最终的排序序列。

//首先假设2个数组是有序的，按照有序序列进行合并，组成有序序列
void merge(int a[],int low ,int mid,int high, int tmp[]) {
    int i = low;       //左子数组开始的位置
    int j = mid + 1;   //右子数组开始的位置
    int t = 0;         //临时空间指针
    //首先 判断要合并的数组的起始位置的大小，然后将数组复制到tmp数组存储。
    // 比较2个数组的每个元素 然后按照大小顺序进行排序。
    while (i <= mid && j <= high) {
	    if (a[i] < a[j]) {
		    tmp[t++] = a[i++];
	    }
	    else
		    tmp[t++] = a[j++];
    }
    //参考https://www.bilibili.com/video/BV1Pt4y197VZ?from=search&seid=6438701192248743313
    //如果右半区就一个元素，上述放好位置后，左半区的元素直接放就好
    //将左边剩余元素填充进temp中
    while (i <= mid) {
        tmp[t++] = a[i++];
    }
    //将右边子数组剩余部分填充到temp中
    while (j <= high) {
        tmp[t++] = a[j++];
    }  
    //将融合后的数据拷贝到原来的数据对应的子空间中
    t = 0;
    while (low <= high) {
        a[low++] = tmp[t++];
    }
}
void Msort(int a[], int low, int high, int tmp[]) {
    if (low < high) {
        int mid = (low + high) / 2;
        //递归划分左半区
        Msort(a,low,mid,tmp);
        //递归划分右半区
        Msort(a,mid + 1,high,tmp);
        //合并左右半区
        merge(a,low,mid,high,tmp);
    }
}

**时间复杂度：**O(NlogN)

**最好时间复杂度：**O(NlogN)

空间复杂度： O(N)

**特点：**时间复杂度于数据是否有序的状况无关。是稳定排序算法。它是高级排序算法中，唯一一个稳定的排序算法。

**应用：**要求排序稳定，空间不重要，则使用归并算法

七、选择排序⭐⭐⭐⭐

//选择排序 
//稳定性最好的排序之一，时间复杂度为O（n2） 规模越小越好，不占用额外空间  
//在未排序中找最小的，放到起始位置，然后再找最小放到第二位置
void SelectSort(int a[], int len) {
    for (int i = 0; i < len; i++) {
        int minindex = i;
        for (int j = i + 1; j < len; j++) {
            if (a[minindex] > a[j]) {    
                minindex = j;
            }
        }
        swap(a[i],a[minindex]);
    }
}

最佳的时候：时间复杂度O( $n^2$ )

最差的时候：时间复杂度O( $n^2$ )

一般情况：时间复杂度O( $n^2$ )

稳定性：不稳定

空间复杂度：O(n)

八、快速排序⭐⭐⭐⭐⭐

//快速排序
//选出一个数作为基准，使得数组左边的小于基准，右边的大于基准
//递归划分

//划分函数
int partion(int a[], int low, int high) {
    //选择第一个元素作为标准
    int index = a[low];
    //推动左右指针向中间移动，
    while (low < high) {
        //如果右边的数比标准大，不用移动，否则交换到左边
        while ((low < high) && a[high] >= index) {
            high--;
        }
        while ((low < high) && a[low] <= index) {
            low++;
        }
        swap(a[low],a[high]);
    }

}

void Qsort(int a[], int low,int high) {
    if (low < high) {
        int index = partion(a,low,high);
        //递归划分
        Qsort(a,low,index - 1);
        Qsort(a,index,high);
    }
}

**时间复杂度：**O( $n l o g n$ )

**最好时间复杂度：O( $n l o g n$ ) ——对应——（额外）空间复杂度：**O( $o g n$ )