【机器学习02】梯度下降

【机器学习02】梯度下降

梯度下降是一个用来求函数最小值的算法，我们将使用梯度下降算法来求出代价函数$J(w,b)$的最小值。
梯度下降背后的思想是：开始时我们随机选择一个参数的组合(θ_0,θ_1,…,θ_n )，计算代价函数，然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到到到一个局部最小值（local minimum），因为我们并没有尝试完所有的参数组合，所以不能确定我们得到的局部最小值是否便是全局最小值（global minimum），选择不同的初始参数组合，可能会找到不同的局部最小值。

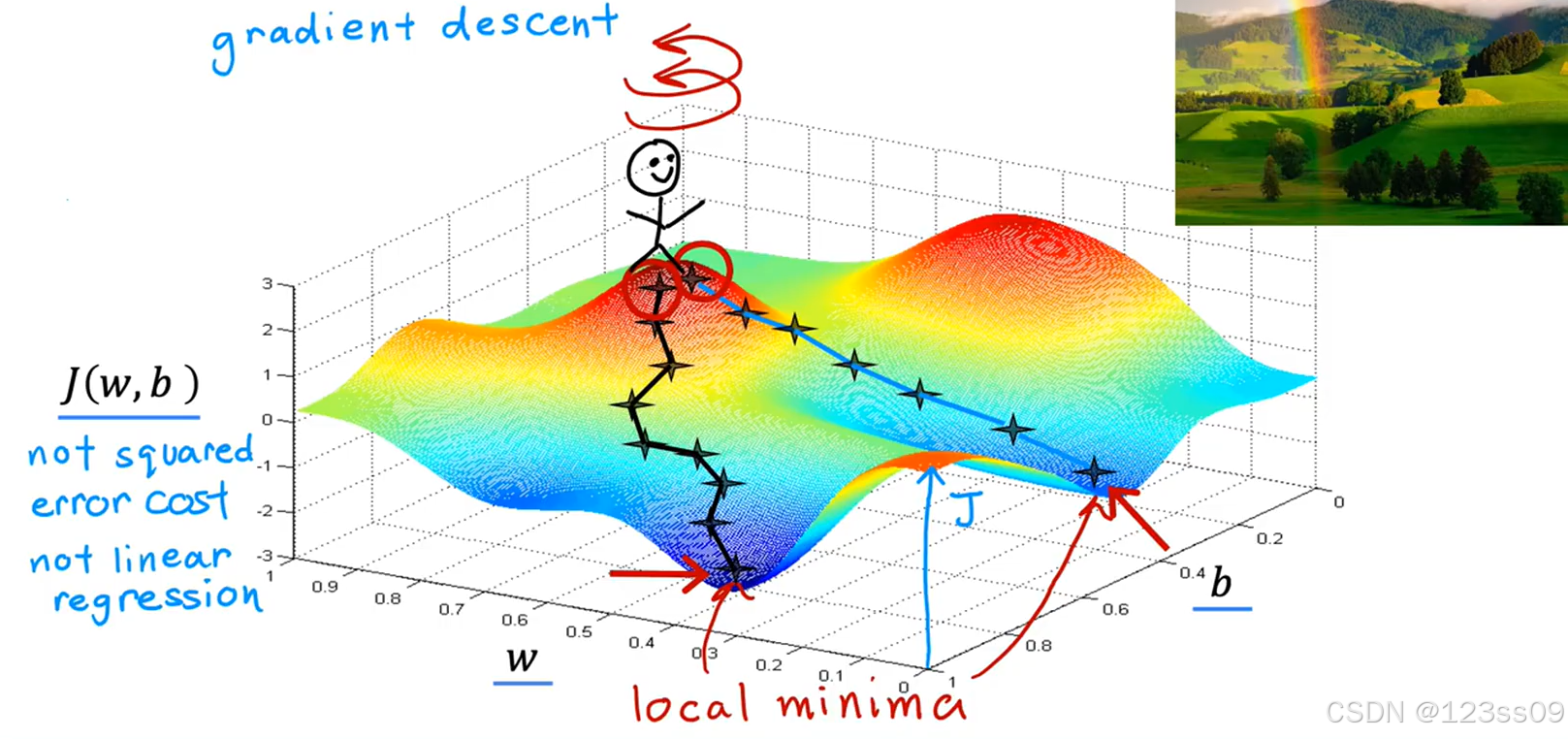
梯度下降算法更新步骤

1. 重复直到收敛

$$\text{Repeat until convergence}$$

2. 更新公式

$$w=w-\alpha \frac{\partial }{\partial w}J(w,b)$$
$$b=b-\alpha \frac{\partial }{\partial b}J(w,b)$$

3. 同步更新

$$\text{temp\_w}=w-\alpha \frac{\partial }{\partial w}J(w,b)$$
$$\text{temp\_b}=b-\alpha \frac{\partial }{\partial b}J(w,b)$$
$$w=\text{temp\_w}$$
$$b=\text{temp\_b}$$

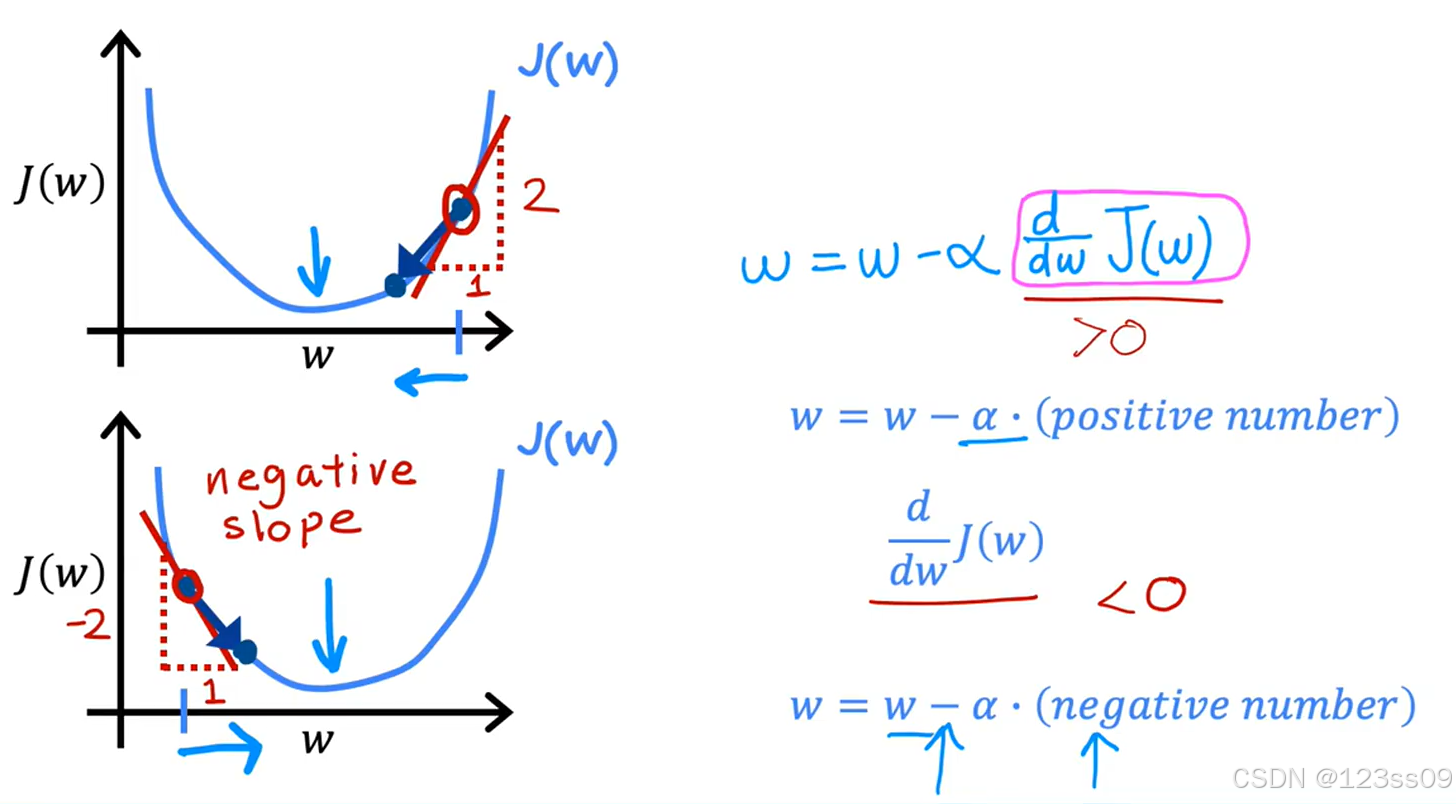
4. 强调内容

• ​学习率：$\alpha$ 控制每次更新的步长。
• ​导数：偏导数表示成本函数在当前参数下的变化率。
• ​同时更新：必须同时更新 $w$ 和 $b$。

向量表示

进阶

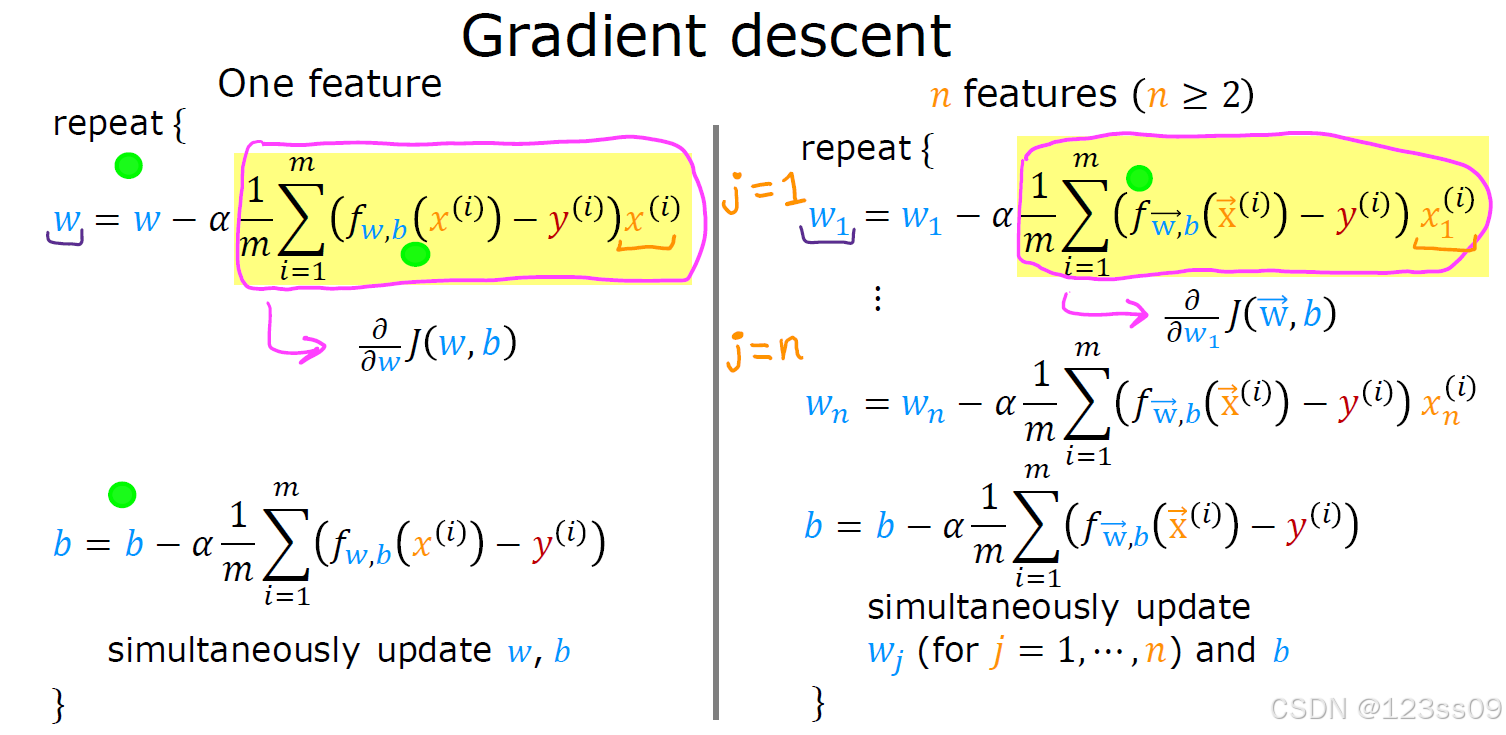
梯度下降算法更新步骤-进阶

1. 单特征

$$w=w-\alpha \frac{1}{m}\sum _{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)})x^{(i)}$$
$$b=b-\alpha \frac{1}{m}\sum _{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)})$$

2. 多特征

$$w_j=w_j-\alpha \frac{1}{m}\sum _{i=1}^m(f_{\vec{w},b}({\vec{x}}^{(i)})-y^{(i)})x_j^{(i)}$$
$$b=b-\alpha \frac{1}{m}\sum _{i=1}^m(f_{\vec{w},b}({\vec{x}}^{(i)})-y^{(i)})$$

3. 同步更新

• 单特征：同时更新 $w$ 和 $b$。
• 多特征：同时更新 $w_j$（$j=1,\dots ,n$）和 $b$。

4. 示例

• 初始化：$w=0$，$b=0$
• 学习率：$\alpha =0.1$
• 更新后：$w=0.5$，$b=0.3$