leedcode 不同路径

最新推荐文章于 2024-09-06 16:32:48 发布

原创最新推荐文章于 2024-09-06 16:32:48 发布 · 95 阅读

0 ·

CC 4.0 BY-SA版权

leedcode 专栏收录该内容

50 篇文章

订阅专栏

本文介绍了一种使用动态规划(DP)算法解决从左上角到右下角的网格路径问题的方法。对于第一行和第一列的格子，由于只能通过竖直或水平方向到达，因此它们的路径数为1。对于其他格子，其路径数等于其左侧和上方格子路径数之和。通过构建二维数组存储每个格子的路径数，最终返回右下角格子的路径数。

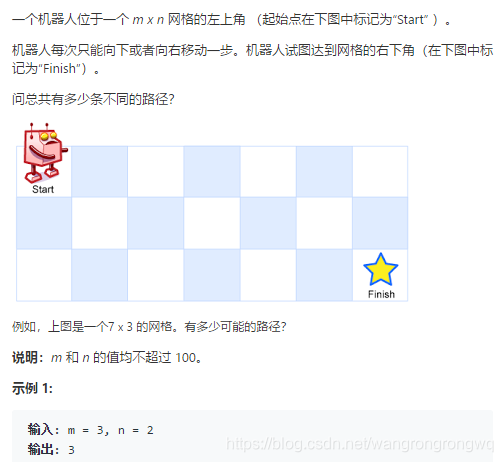
使用dp，对于第一行和第一列的格子，只能有一个方法到达，要不是竖着走，要不横着走。其他的各自的走法只与其左边和上边的格子走法有关，即两个格子走法之和，即a[i][j]=a[i-1][j]+a[i][j-1]

class Solution(object):
    def uniquePaths(self, m, n):
        """
        :type m: int
        :type n: int
        :rtype: int
        """
        a = []
        for i in range(m):
            temp = []
            for j in range(n):
                temp.append(0)
            a.append(temp)
        for i in range(m):
            a[i][0] = 1
        for j in range(n):
            a[0][j] = 1
        for i in range(1, m):
            for j in range(1, n):
                a[i][j] = a[i - 1][j] + a[i][j - 1]
        return a[m - 1][n - 1]